二叉搜索树的插入、删除、查找的递归实现
二叉搜索树的递归实现
首先,二叉搜索树是也是一颗二叉树。它的特点是左结点(左子树的根结点)的值比根结点小,右结点的值比根结点的值大。比如说,下图所示的二叉搜索树:
所以我们定义二叉搜索树的结构如下:
#pragma once
#include
#include
#define SHOW_NAME printf("\n==============%s=================\n", __FUNCTION__);
typedef char SearchNodeType;
//二叉搜索树结点
//二叉搜索树的左结点一定小于根结点,根结点一定小于右结点
typedef struct SearchNode
{
SearchNodeType data;
struct SearchNode* lchild;
struct SearchNode* rchild;
}SearchNode;
1. 初始化
//1.初始化
void SearchTreeInit(SearchNode** proot)//初始化
{
if(proot == NULL)//非法输入
return;
*proot = NULL;//用空指针初始化
return;
}
2. 销毁
//2.销毁(递归实现)
void SearchNodeDestroy(SearchNode* node)//销毁结点
{
free(node);
}
void SearchTreeDestroy(SearchNode** proot)//销毁树
{
if(proot == NULL)//非法操作
return;
if(*proot == NULL)//空树
return;
SearchNode* root = *proot;
SearchTreeDestroy(&root->lchild);
SearchTreeDestroy(&root->rchild);
SearchNodeDestroy(root);
*proot = NULL;
return;
}
3. 打印函数,用于测试
//3.打印函数(这里是先序遍历)
void SearchTreePrint(SearchNode* root)//打印函数,用于测试
{
if(root == NULL)//空树,也是递归遍历结束条件
return;
SearchNode* cur = root;
printf("[%c] ", root->data);
SearchTreePrint(cur->lchild);
SearchTreePrint(cur->rchild);
return;
}
4. 给定一个值,插入该值到二叉搜索树中
这里要注意的就是,我们不能不能任意位置插入该元素,因为我们要保证插入该元素之后,它
依旧满足二叉搜索树的定义。
并且我们约定该二叉搜索树中不能存在相同元素,所以若要插入元素在二叉搜索树中已存在,就直接返回,表示插入失败。
先查找合适的插入位置:
若插入值小于当前结点的值,就向当前结点的左子树找;若插入值大于当前结点的值,就向当前结点的右子树找;或者当前结点为空,就可以进行插入了。
//4.插入结点(递归实现)
//注意这里不能指定位置插入,因为要保证插入之后依旧满足二叉搜索树的定义
SearchNode* CreateSearchNode(SearchNodeType value)//创建一个结点
{
SearchNode* new_node = (SearchNode*)malloc(sizeof(SearchNode));
new_node->data = value;
new_node->lchild = NULL;
new_node->rchild = NULL;
return new_node;
}
void SearchTreeInsert(SearchNode** proot, SearchNodeType to_insert)
{
if(proot == NULL)//非法输入
return;
//空树,可直接插入指针指向的位置
if(*proot == NULL)
{
SearchNode* new_node = CreateSearchNode(to_insert);
*proot = new_node;
return;
}
//非空树
SearchNode* cur = *proot;
//递归向左子树插入
if(to_insert < cur->data)
{
SearchTreeInsert(&cur->lchild, to_insert);
}
//递归向右子树插入
else if(to_insert > cur->data)
{
SearchTreeInsert(&cur->rchild, to_insert);
}
//插入值已在二叉搜索树中存在
else
{
//关于“等于”的处理办法有许多
//我们约定在该二叉搜索树中,元素不能重复,所以遇到相等情况,不做任何操作,直接返回。表示插入失败
//也可以约定为:放入相同元素左子树的最右边,或者右子树的最左边
return;
}
return;
}
5. 给定一个值,查找它在二叉搜索树中对应的结点
找到返回结点,找不到返回NULL。
若查找值小于当前结点的值,就向当前结点的左子树找;
若查找值大于当前结点的值,就向当前结点的右子树找;直至找到就返回结点,或者当前结点为空,表示查找失败。
//5.查找结点(递归):给定一个值,查找对应结点
SearchNode* SearchTreeFind(SearchNode* root, SearchNodeType to_find)//查找指定值结点
{
if(root == NULL)//空树,也是没找到的条件
return NULL;
//找到了
if(to_find == root->data)
return root;
//递归查找左子树
if(to_find < root->data)
{
return SearchTreeFind(root->lchild, to_find);
}
//递归查找右子树
if(to_find > root->data)
{
return SearchTreeFind(root->rchild, to_find);
}
}
6. 给定一个值,在二叉搜索树中删除对应结点
首先查找对应结点,找到之后分组讨论:
(1)要删除的结点无左右子树,可直接删除释放;
(2)
要删除的结点仅有左子树,将它的左子树与父结点连接上,即可删除释放;
(3)要删除的结点仅有右子树,将它的右子树与父结点连接上,即可删除释放;
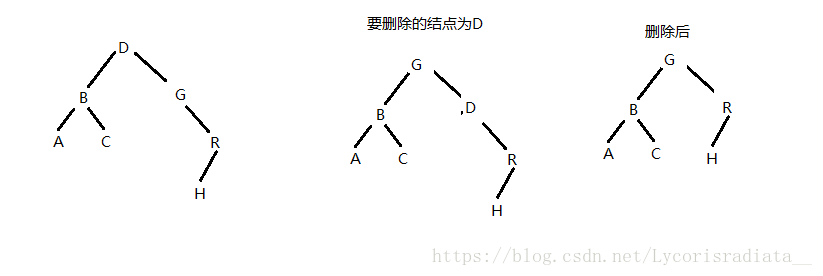
(4)要删除的结点有左右子树,可以找到它右子树的最小值,用最小值覆盖要删除结点的值,再删除最小值结点,相当于删除了要删除的结点。这里删除最小值结点相当于删除一个无子树的结点。具体情况见下图:
//6.删除结点(递归):给定一个值,删除对应结点
//这里不用担心有相同元素,我们约定该二叉搜索树中不存在相同元素
void SearchTreeRemove(SearchNode** proot, SearchNodeType to_remove)//删除指定值结点
{
if(proot == NULL)//非法操作
return;
//1.没找到该元素
if(*proot == NULL)//空树,也是没找到的条件
return;
//2.查找元素
SearchNode* cur = *proot;
if(to_remove < cur->data)
{
SearchTreeRemove(&cur->lchild, to_remove);
return;
}
else if(to_remove > cur->data)
{
SearchTreeRemove(&cur->rchild, to_remove);
return;
}
//3.删除元素,此时cur指向即为要删除的结点
else
{
SearchNode* ret = cur;//ret即为要删除的结点
//(1)要删除结点无子树->直接删除释放
if(ret->lchild == NULL && ret->rchild == NULL)
{
*proot = NULL;//当前的*poot即为要删除的结点,因为是递归调用的
SearchNodeDestroy(ret);
return;
}
//(2)要删除的结点仅有左子树->让父结点指向它的左子树
if(ret->lchild != NULL &&ret->rchild == NULL)
{
*proot = ret->lchild;
SearchNodeDestroy(ret);
return;
}
//(3)要删除的结点仅有右子树->让父结点指向它的右子树
if(ret->lchild == NULL &&ret->rchild != NULL)
{
*proot = ret->rchild;
SearchNodeDestroy(ret);
return;
}
//(4)要删除的结点左右子树都在
if(ret->lchild != NULL && ret->rchild != NULL)
{
//找要删除的结点的右子树的最小值
SearchNode* min = ret->rchild;
while(min->lchild != NULL)
{
min = min->lchild;
}
//将最小值覆盖要删除的结点,删除最小值的结点即可
ret->data = min->data;
//这里删除最小值对应的结点即是删除一个无子树的结点
SearchTreeRemove(&ret->rchild, min->data);
return;
}
}
}
以下为以上函数的
测试代码:
这里要注意,测试函数的正确性时,要考虑到所有可能的情况,并对所有情况都应该测试一次。
void TestInit()
{
SHOW_NAME;
SearchNode* root;
SearchTreeInit(&root);
printf("expected is nil, actual is %p\n", root);
}
void TestDestroy()
{
SHOW_NAME;
SearchNode* root;
SearchTreeInit(&root);
SearchTreeDestroy(&root);
}
void TestInsert()
{
SHOW_NAME;
SearchNode* root;
SearchTreeInit(&root);
SearchTreeInsert(&root, 'd');
SearchTreeInsert(&root, 'g');
SearchTreeInsert(&root, 'a');
SearchTreeInsert(&root, 'r');
SearchTreeInsert(&root, 'b');
SearchTreeInsert(&root, 'k');
SearchTreePrint(root);
printf("\n");
}
void TestFind()
{
SHOW_NAME;
SearchNode* root;
SearchTreeInit(&root);
SearchTreeInsert(&root, 'd');
SearchTreeInsert(&root, 'g');
SearchTreeInsert(&root, 'a');
SearchTreeInsert(&root, 'r');
SearchTreeInsert(&root, 'b');
SearchTreeInsert(&root, 'k');
SearchTreePrint(root);
printf("\n");
SearchNode* ret = SearchTreeFind(root, 'r');
printf("expected is r, actual is %c\n", ret->data);
ret = SearchTreeFind(root, 'h');
printf("expected is nil, actual is %p\n", ret);
}
void TestRemove()
{
SHOW_NAME;
SearchNode* root;
SearchTreeInit(&root);
SearchTreeInsert(&root, 'd');
SearchTreeInsert(&root, 'g');
SearchTreeInsert(&root, 'a');
SearchTreeInsert(&root, 'r');
SearchTreeInsert(&root, 'b');
SearchTreeInsert(&root, 'k');
SearchTreePrint(root);
printf("\n");
//仅有左子树
// SearchTreeRemove(&root, 'r');
// SearchTreePrint(root);
// printf("\n");
//仅有右子树
// SearchTreeRemove(&root, 'g');
// SearchTreePrint(root);
// printf("\n");
//无子树
// SearchTreeRemove(&root, 'k');
// SearchTreePrint(root);
// printf("\n");
//左右子树均在
SearchTreeRemove(&root, 'd');
SearchTreePrint(root);
printf("\n");
}