【Usaco2016 FEB】Load Balancing【线段树 + 二分】

大膜YZ哥

题目大意

给你一个矩阵，里面有些点，让你横向切一刀，纵向切一刀，使得得到的四个区域内的最大的点数最少。

输入

7
7 3
5 5
7 13
3 1
11 7
5 3
9 1

输出

2

分析

• 首先，我们要枚举纵向是从哪里分开（从左往右扫），可以用离散化进行优化。
• 然后，我们需要二分来找一个横向分开的最优位置。我们先假设每次都可以知道从mid分开后，四个区域内每个区域的点数，那么我们便可以知道二分的方法：如果最大值在上方，l=mid，否则，r=mid（边界条件大意是这样，这个赋值不是一定的，可以自己想一下）。
• 那么我们要怎么知道每个区域内的点数呢？我们可以用两个前缀和，sumy[i]表示从x轴标为i的地方纵向分开，左边矩阵点的个数，sumx[j]表示从y轴标为j处横向分开下方矩阵的点数，可以预处理出来。（当然sumy也可在枚举时求出，不用数组）
• 因此，在二分时，我们可以很快（O(1)）的时间内求出point(b+c)和point(c+d)的值。然而现在我们还是不知道每个区域的点数。于是我们又可以用一个线段树来存所有在i（枚举的纵向分开的地方）左边的点，加入的时候按照纵坐标加入。
• 
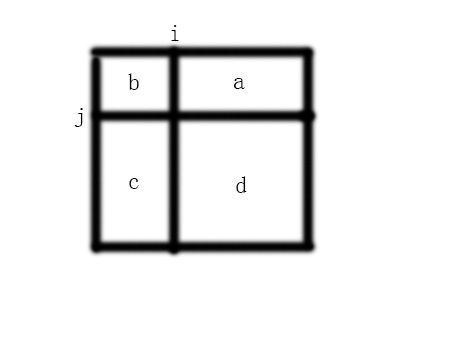
• 当时我在做的时候，我想，这不是在二维中的线段树吗？而线段树是在一维查询的，感到很奇怪。但是，如果我们每次在枚举i的时候，将左方矩阵中新出现的点加入进线段树中的话，线段树其实是一维的。为什么呢？因为当我们在二分的时候，想知道c区域内的点数，这个区域的左右边界显然不会再改变，只有上下边界会变（确切的说只有上边界），我们将线段树中每个节点的定义改为：在这个左右边界的条件下，这一层有多少个点（即有多少个y坐标为k的点）， 那么这样一来，就变成一维线段树了。问题就此解决。

#include
#include

#include

using namespace std;
const int INF = 0xfffffff;
const int maxn = 500000 + 10;
const int maxm = 100000 + 10;
int srchq[maxn], prex[maxn], prey[maxn], left, right, down, up, n, cnt, ok, x, y;
bool exist[maxn];
//struct poi{
//  int x, y;
//}point[maxm];

vector<int> which[maxn];
int node[4 * maxn];

void Insert(int l, int r, int now, int aim){
    node[now] ++;
    if(l == r)
        return;
    int m = (l + r) / 2;
    if(aim > m)
        Insert(m + 1, r, now * 2 + 1, aim);
    else
        Insert(l, m, now * 2, aim);
}

void Query(int al, int ar, int l, int r, int now){
    int m = (l + r) / 2;
    if(al <= l && ar >= r)
        ok += node[now];
    else{
        if(al <= m)
            Query(al, ar, l, m, now * 2);
        if(ar > m)
            Query(al, ar, m + 1, r, now * 2 + 1);
    }
}

void Readin(){
    left = down = INF;
    right = up = -INF;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++){
        scanf("%d %d", &x, &y);
        left = min(left, (x + 1) / 2);
        right = max(right, (x + 1) / 2);
        down = min(down, (y + 1) / 2);
        up = max(up, (y + 1) / 2);
        prex[(x + 1) / 2] ++;
        prey[(y + 1) / 2] ++;
        if(!exist[(y + 1) / 2]){
            exist[(y + 1) / 2] = 1;
            srchq[++ cnt] = (y + 1) / 2;
        }

        which[(y + 1) / 2].push_back((x + 1) / 2);

    }
}

void Calcpre(){
    for(int i = left; i <= right; i ++)
        prex[i] += prex[i - 1];
    for(int i = down; i <= up; i ++)
        prey[i] += prey[i - 1];
}

void Init(){
    scanf("%d", &n);
    left = down = INF;
    right = up = -INF;
    Readin();
    Calcpre();
}

//int Calcpoint(int right, int up){
//  int tmp = 0;
//  for(int i = 1; i <= n; i ++)
//      if(point[i].x < right && point[i].y < up)
//          tmp ++;
//  return tmp;
//}

//int Three(int i){
//  int l = left, r = right, brk1, brk2, ans1, ans2, tmp;
//  while(l < r){
//      brk1 = l + (r - l) / 3;
//      brk2 = r - (r - l) / 3;
//      tmp = Calcpoint(brk1, i);
//      ans1 = max(prey[i] - tmp, max(prex[brk1] - tmp, max(tmp, n - (prey[i] + prex[brk1] - tmp))));
//      tmp = Calcpoint(brk2, i);
//      ans2 = max(prey[i] - tmp, max(prex[brk2] - tmp, max(tmp, n - (prey[i] + prex[brk2] - tmp))));
//      if(ans1 < ans2)
//          r = brk2 - 1;
//      else
//          l = brk1 + 1;
//  }
//  return r;
//}
//void Solve(){
//  int ans = INF;
//  for(int i = down + 1; i < up; i += 2)
//      ans = min(ans, Three(i));
//  printf("%d", ans);
//}

//int Calcpoint(int right, int up){
//  int tmp = 0;
//  for(int i = 1; i <= n; i ++)
//      if(point[i].x < right * 2 && point[i].y < up * 2)
//          tmp ++;
//  return tmp;
//}

//int Three(int i){
//  int l = left, r = right, brk1, brk2, ans1, ans2, tmp;
//  while(l < r){
//      brk1 = l + (r - l) / 3;
//      brk2 = r - (r - l) / 3;
//      tmp = Calcpoint(brk1, i);
//      ans1 = max(max(max(n - (prex[brk1] + prey[i] - tmp), prex[brk1] - tmp), tmp), prey[i] - tmp);
//      tmp = Calcpoint(brk2, i);
//      ans2 = max(max(max(n - (prex[brk2] + prey[i] - tmp), prex[brk2] - tmp), tmp), prey[i] - tmp);
//      if(ans1 < ans2)
//          r = brk2 - 1;
//      else
//          l = brk1 + 1;
//  }
//  tmp = Calcpoint(r, i);
//  return max(max(max(n - (prex[r] + prey[i] - tmp), prex[r] - tmp), tmp), prey[i] - tmp);
//}

int Two(int i){
    int lmax, rmax, l = left, r = right - 1, m, tmp;
    while(l < r){
        m = (l + r) / 2;
//      tmp = Calcpoint(m, i);
        ok = 0;
        Query(left - 1, m, left - 1, right, 1);
        tmp = ok;
        lmax = max(tmp, prex[m] - tmp);
        rmax = max(prey[i] - tmp, n - (prex[m] + prey[i] - tmp));
        if(lmax < rmax)
            l = m + 1;
        else
            if(lmax == rmax){
                r = m;
                break;
            }
            else
                r = m - 1;
    }
    ok = 0;
    Query(left - 1, r, left - 1, right, 1);
    tmp = ok;
    lmax = max(tmp, prex[r] - tmp);
    rmax = max(prey[i] - tmp, n - (prex[r] + prey[i] - tmp));
    return max(lmax, rmax);
}

void Solve(){
    int ans = INF;
    sort(srchq + 1, srchq + cnt + 1);
//  for(int i = down; i <= up; i ++)
    for(int i = 1; i <= cnt - 1; i ++){
        for(int j = 0; j < which[srchq[i]].size(); j ++)
            Insert(left - 1, right, 1, which[srchq[i]][j]);
//      ans = min(ans, Three(srchq[i]));
        ans = min(ans, Two(srchq[i]));
    }
    printf("%d", ans);
}

int main(){
    freopen("balancing.in", "r", stdin);
    freopen("balancing.out", "w", stdout);

    Readin();
    Calcpre();

    Solve();
    return 0;
}