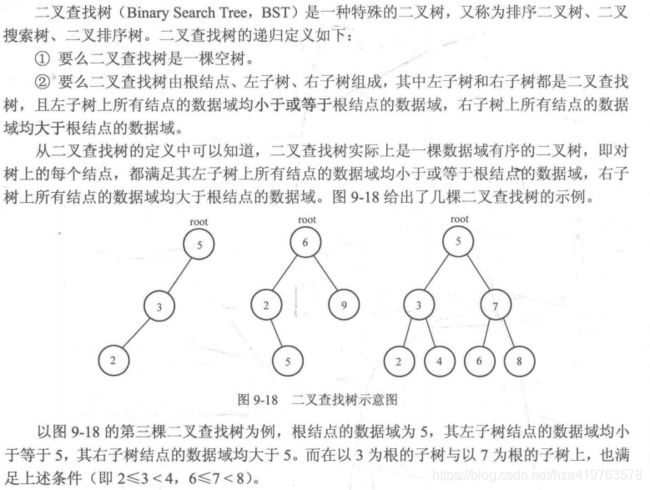
9.4.1 二叉查找树的定义
定义结构:
struct node{
int data;
node *lchild,*rchild;
};
node* newNode(int x){
node* Node=new node;
Node->data=x;
Node->lchild=Node->rchild=NULL;
return Node;
}
1.查找操作

//search函数查找二叉查找树中数据域为x的结点
void search(node* root,int x){
if(root==NULL){
cout<<"查找失败!"<data){
cout<data<data){//比根结点小 在左子树
search(root->lchild,x);
}else{//比根结点大 在右子树
search(root->rchild,x);
}
}
2.插入操作

//插入一个数据域为x的新结点 (注意参数root要加引用&)
void insert(node* &root,int x){
if(root==NULL){//空树,说明查找失败,也即插入位置
root=newNode(x);
return;
}
if(x==root->data) return;//结点已经存在 不需要插入(二叉查找树元素一定不会重复)
else if(xdata) insert(root->lchild,x);
else insert(root->rchild,x);
}
3.二叉树的建立
//二叉查找树的建立 直接插入即可
//注意相同数字 插入顺序不同 生成的二叉查找树也可能不同
node* Create(int data[],int n){
node* root=NULL;
for(int i=0;i
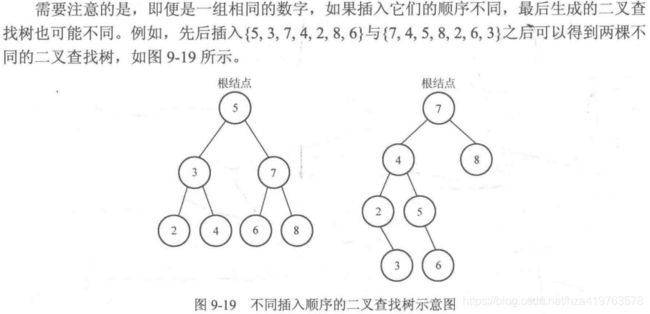
4.二叉查找树的删除(难点)

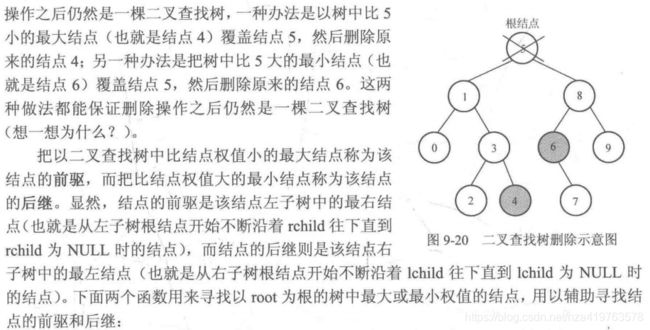
//二叉查找树的删除 难点
//寻找以root为根结点的树中的最大权值结点
node* findMax(node* root){
while(root->rchild!=NULL) root=root->rchild;//不断往右 直到没有右孩子 就是权值最大的结点
return root;
}
//寻找以root为根结点的树中的最小权值结点
node* findMin(node* root){
while(root->lchild!=NULL) root=root->lchild;//不断往左 直到没有左孩子 就是权值最小的结点
return root;
}


//删除以root为根结点的树中权值为x的结点
void deleteNode(node* &root,int x){
if(root==NULL) return;//能走到死胡同 说明不存在权值为x的结点
if(root->data==x){
if(root->lchild==NULL&&root->rchild==NULL){//叶子结点 直接删除
root=NULL;
}else if(root->lchild!=NULL){
node* pre=findMax(root->lchild);
root->data=pre->data;//用前驱覆盖root
deleteNode(root->lchild,pre->data);//左子树中删除前驱
}else{
node* next=findMin(root->rchild);
root->data=next->data;//用前驱覆盖root
deleteNode(root->rchild,next->data);//左子树中删除前驱
}
}else if(root->data>x){
deleteNode(root->lchild,x);//在左子树中删除x
}else{
deleteNode(root->rchild,x);//在右子树中删除x
}
}

9.4.3 二叉查找树的性质


代码总结:
#include
using namespace std;
struct node{
int data;
node *lchild,*rchild;
};
node* newNode(int x){
node* Node=new node;
Node->data=x;
Node->lchild=Node->rchild=NULL;
return Node;
}
//search函数查找二叉查找树中数据域为x的结点
void search(node* root,int x){
if(root==NULL){
cout<<"查找失败!"<data){
cout<data<data){//比根结点小 在左子树
search(root->lchild,x);
}else{//比根结点大 在右子树
search(root->rchild,x);
}
}
//插入一个数据域为x的新结点 (注意参数root要加引用&)
void insert(node* &root,int x){
if(root==NULL){//空树,说明查找失败,也即插入位置
root=newNode(x);
return;
}
if(x==root->data) return;//结点已经存在 不需要插入(二叉查找树元素一定不会重复)
else if(xdata) insert(root->lchild,x);
else insert(root->rchild,x);
}
//二叉查找树的建立 直接插入即可
//注意相同数字 插入顺序不同 生成的二叉查找树也可能不同
node* Create(int data[],int n){
node* root=NULL;
for(int i=0;irchild!=NULL) root=root->rchild;//不断往右 直到没有右孩子 就是权值最大的结点
return root;
}
//寻找以root为根结点的树中的最小权值结点
node* findMin(node* root){
while(root->lchild!=NULL) root=root->lchild;//不断往左 直到没有左孩子 就是权值最小的结点
return root;
}
//删除以root为根结点的树中权值为x的结点
void deleteNode(node* &root,int x){
if(root==NULL) return;//能走到死胡同 说明不存在权值为x的结点
if(root->data==x){
if(root->lchild==NULL&&root->rchild==NULL){//叶子结点 直接删除
root=NULL;
}else if(root->lchild!=NULL){
node* pre=findMax(root->lchild);
root->data=pre->data;//用前驱覆盖root
deleteNode(root->lchild,pre->data);//左子树中删除前驱
}else{
node* next=findMin(root->rchild);
root->data=next->data;//用前驱覆盖root
deleteNode(root->rchild,next->data);//左子树中删除前驱
}
}else if(root->data>x){
deleteNode(root->lchild,x);//在左子树中删除x
}else{
deleteNode(root->rchild,x);//在右子树中删除x
}
}
void preorder(node* root){
if(root==NULL) return;
cout<data<<" ";
preorder(root->lchild);
preorder(root->rchild);
}
int main(){
freopen("input.txt","r",stdin);
const int N=8;
int a[8]={3,4,8,7,1,2,10,23};
node* root=Create(a,8);
preorder(root);
cout<










