leetcode 518. Coin Change 2找零钱的方案数-动态规划

题目描述：

链接：https://www.nowcoder.com/questionTerminal/185dc37412de446bbfff6bd21e4356ec
来源：牛客网
 

有一个数组changes，changes中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，对于一个给定值x，请设计一个高效算法，计算组成这个值的方案数。

给定一个int数组changes，代表所有零钱，同时给定它的大小n，另外给定一个正整数x，请返回组成x的方案数，保证n小于等于100且x小于等于10000。

测试样例：

[5,10,25,1],4,15

返回：6

测试样例：

[5,10,25,1],4,0

返回：1

解题思路：（实质上是一个0-1背包问题）

参考：https://www.nowcoder.com/questionTerminal/185dc37412de446bbfff6bd21e4356ec

对于找零问题有两个版本，一个是求找零后零钱的数量最少；另一个就是本题，求找零的方案数。

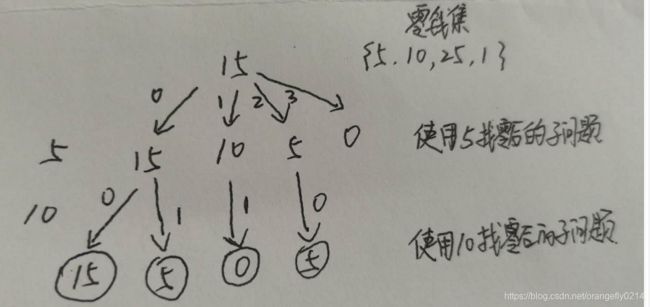
求解思路：
使用0个｛5｝时，求解子问题 X - 0 * 5 在 ｛10，25，1｝的方案数
使用1个｛5｝时，求解子问题 X - 1 * 5 在 ｛10，25，1｝的方案数
使用2个｛5｝时，求解子问题 X - 2 * 5 在 ｛10，25，1｝的方案数
……
把上面的方案是加起来就是所求的结果了，但是注意边界: 对 0 找零的方案数为 1。

根据上面分析，可以将问题转换为递归，或者用一维dp数组实现。

 

实现1：（递归）

public int recursion(int[] changes,int begin,int end,int target){
	//边界条件
	if(target==0){
		return 1;
	}
	if(begin>end||target<0){
		return 0;
	}
	int count=0;
	int times=0;
	//找零过程中使用了times次的changes[begin]
	//在后续找零过程中不再使用changes[begin]
	while(times*changes[begin]<=target){
		count+=recursion(changes, begin+1, end, target-times*changes[begin]);
		++times;
	}
	return count;
}

迭代版本：

对应的情况是：

i=0 changes[i]=5； j=6,7,8,9,10,11,12,13,14,15

i=1 changes[i]=10; j=11,12,13,14,15

i=2 changes[i]=25 此时没有满足条件的j,面值大于需要找零的总值

i=3 changes[i]=1; j=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15

public int countWays(int[] changes, int n, int x) {
	int[] dp=new int[x+1];
	dp[0]=1;//dp[i]表示凑成i有多少种方案
	for(int i=0;i

 

实现2：（0-1背包问题求解）

详细解释参考视频https://www.youtube.com/watch?v=DJ4a7cmjZY0

动态规划求解，dp[j]表示凑成j的方案数，

dp[j+changes[i]] += dp[j];  （j从0到15表示第几列，change[i]表示加入的零钱，大致过程如下：

下图行表示金额j,列表示硬币changes[0-n]

 

public int countWays3(int[] changes, int n, int x) {
	//dp[i][j]表示使用changes[0][i]的钱币组成金额j的方法数
	int[][] dp=new int[n][x+1];
	//第一列全为1，因为组成金额0只有一种方法
	for(int i=0;i=0?dp[i][j-changes[i]]:0);
		}
	}
	return dp[n-1][x];
	
}

 

实现3：

这是一个经典的背包问题，

 dp[i][j]:表示用前i种硬币组成金额j的组合数。
状态转移：

（1）不使用第i个coin，仅仅使用前i-1种coin来组成金额j,此时有dp[i-1][j]种方法。
（2）使用第i个coin，因为相同的硬币可以无限使用，所以我们需要知道通过使用前i种硬币（包括第i种），
有多少种方法来组成j-coins[i-1]，表示为dp[i][j-coins[i-1]]
初始化：dp[i][0]=1表示任何一种硬币对0的找零都为1

public int change(int amount, int[] coins) {
	int n=coins.length;
	int x=amount;
	int[][] dp = new int[n+1][x+1];
	dp[0][0] = 1;

	for (int i = 1; i <=n; i++) {
		dp[i][0] = 1;
		for (int j = 1; j <= x; j++) {
			dp[i][j] = dp[i-1][j] + (j >= coins[i-1] ? dp[i][j-coins[i-1]] : 0);
		}
	}
	return dp[n][x];
}

空间优化：dp[i][j]仅仅依赖于dp[i-1][j]和dp[i][j-coins[i-1]],所以我们可以使用一维数组做空间优化。（采用）

 public int change2(int amount, int[] coins) {
	int[] dp = new int[amount + 1];
	dp[0] = 1;
	for (int i=0;i