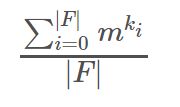群、置换群、Burnside引理和Polya定理学习及相关习题练习

群：  设G是一个集合，*是G上的二元运算，如果(G,*)满足下面的条件：

封闭性：对于任何a,b∈G,有a*b∈G;

结合律：对任何a,b,c∈G有(a*b)*c=a*(b*c);

单位元：存在e∈G,使得对所有的a∈G,都有a*e=e*a=a;

逆元：对于每个元素a∈G,存在x∈G,使得a*x=x*a=e,这个时候记x为a-1，称为a的逆元，那么则称(G,*)为一个群。

 

例：G={0,1,2,3,4....n-1}那么它在mod n加法下是一个群。

群元素的个数有限，称为有限群，且其中元素的个数称为阶，记为|G|,群元素的个数无限，称为无限群。

即 几个元素就为几阶

============================================================================================

置换定义：

设X为一个有限集，π是X到X的一个--变换，那么称π是X上的一个置换。

例：设X={1,2,3,4....n},设π是X的一个变换，满足π：1->a1,2->a2,......n->an,其中a1,a2...an是X的一个排列，则称π是X上的一个置换。

可将π记为   1     2   ......   n    

                  a1   a2   ......a n    

同一置换用这样的表示法有n!种，但其对应的关系不变。

假设循环π只这样一个置换，满足π：a1->a2,a2->a3,.............ak->a1,但是对于其他元素保持不变，即：a->a,

可将π记为   a1     a2   ......   ak    

                  a2   a3   ......  a1     

称为k阶循环，K为循环长度。

每个置换都可以写成若干个互不相交的循环的乘积，且表示是唯一的.

如   1   2  3   4  5  6    

       2   4   5  1  3  6    ，则可以表示为(124)(35)(6),置换的循环节数是上面的循环个数，上面的例题的循环节数为3.

============================================================================================

定义：设G是有限集X上的置换群，点a,b∈X称为"等价"的，当且仅当，存在π∈G使得π(a)=b，记为a~b，这种等价条件下，X的元素形成的等价类称为G的轨道，它是集X的一个子集，G的任意两个不同的轨道之交是空集，所以置换群G的轨道全体是集合X的一个划分，构成若干个等价类，等价类的个数记为L。

Zk (K不动置换类)：设G是1…n的置换群。若K是1…n中某个元素，G中使K保持不变的置换的全体，记以Zk，叫做G中使K保持不动的置换类，简称K不动置换类。

Ek(等价类)：设G是1…n的置换群。若K是1…n中某个元素，K在G作用下的轨迹，记作Ek。即K在G的作用下所能变化成的所有元素的集合。.

这个时候有：|Ek|*|Zk|=|G|成立(k=1,2,.....n)。

C(π)：对于一个置换π∈G,及a∈X，若π(a)=a，则称a为π的不动点。π的不动点的全体记为C(π)。例如π=(123)(3)(45)(6)(7)，X={1,2,3,4,5,6,7};那么C(π)={3,6,7}共3个元素。

============================================================================================

BurnsideBurnside引理： 
对于一个置换ff,若一个染色方案ss经过置换后不变，称ss为ff的不动点。将ff的不动点数目记为C(f)C(f)，则可以证明等价类数目为所有C(f)C(f)的平均值。

即     

          

用百度百科的例子进行演示： 
一正方形分成44格，22着色，有多少种方案？其中，经过转动相同的图象算同一方案。

对于每种格子我们都有两种选择，所以会有一下16种方案：
 
但是对于这16种方案可以归一下类： 
Θ不动：a1=(1)(2)…(16) 
Θ逆时针转90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16) 
Θ顺时针转90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13) 
Θ转180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16) 
(a,b,c)(a,b,c)表示a,b,ca,b,c可以通过旋转得到。 
由BurnsideBurnside引理，共有(16+2+2+4)4=6(16+2+2+4)4=6(种方案). 

burnside是一种计数方法，用来计算含有不等价类的数量 
burnside算法的关键是找好“置换群”。 

POJ 2154 
PE 281

polya定理 :
polya定理实际上是burnside引理的具体化，提供了计算不动点的具体方法。 
假设一个置换有k个循环，易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。因此，如果有m种可选颜色，则该置换对应的不动点个数为mk。用其替换burnside引引理中的C(f)，。得到等价类数目为：

其中|F|表示置换的数目，ki表示第i个置换包含的循环个数。

 
还是这个例子吧。

Θ不动：a1=(1)(2)(3)(4) 
Θ旋转90度 ：a2=(1 2 3 4) 
Θ旋转180度 ：a3=(1 3)(2 4) 
Θ旋转270度：a4=(1 4 3 2) 
比如，“逆时针旋转180度”，这个置换写成循环的乘积就是（1,3）（2,4），即1和3互变，2和4互变，不难发现，1和3的颜色必须相同，2和4的颜色也必须相同，而1-3和2-4的颜色互不相干。 
由Polya定理得，共有=6(种方案). 
可以看Burnside引理和PolyaPolya定理是一样的，Polya定理是Burnside引理的优化。

 

POJ 1286