计算几何OJ 答案集

作为新手的我 以下为收录和总结的一些编程题答案有问题请及时留言 或者遇到新的问题请留言 会不断更新

A - 线段相交

给出平面上两条线段的两个端点，判断这两条线段是否相交（有一个公共点或有部分重合认为相交）。 如果相交，输出"Yes"，否则输出"No"。

• Input

第1行：一个数T，表示输入的测试数量(1 <= T <= 1000) 第2 - T + 1行：每行8个数，x1,y1,x2,y2,x3,y3,x4,y4。(-10^8 <= xi, yi <= 10^8) (直线1的两个端点为x1,y1 | x2, y2,直线2的两个端点为x3,y3 | x4, y4)

• Output

输出共T行，如果相交输出"Yes"，否则输出"No"。

• Sample Input

2
1 2 2 1 0 0 2 2
-1 1 1 1 0 0 1 -1

• Sample Output

Yes
No

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        double x1,x2,y1,y2,x3,x4,y3,y4,k1,k2;
        double w1,w2,w3,w4;
        int flag=0;
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
        if((x2-x1)==0)              //如果斜率不存在
        {
            if((x3>=x2&&x4<=x2)||(x4>=x2&&x3<=x2))
                flag+=1;
        }
        else                    //如果存在
        {
            k1=(double)(y2-y1)/(x2-x1);
            w3=k1*(x3-x2)+y2;
            w4=k1*(x4-x2)+y2;
            if((y3>=w3&&y4<=w4)||(y3<=w3&&y4>=w4))      //看图模拟
                flag+=1;
        }
        if((x4-x3)==0)                  //继续判断斜率是否存在
        {
            if((x2>=x3&&x1<=x3)||(x1>=x3&&x2<=x3))
                flag+=1;
        }
        else
        {
            k2=(double)(y4-y3)/(x4-x3);
            w1=k2*(x1-x3)+y3;
            w2=k2*(x2-x3)+y3;
            if((y2>=w2&&y1<=w1)||(y2<=w2&&y1>=w1))
                flag+=1;
        }
        if(flag==2)
            printf("Yes\n");
        else
            printf("No\n");
    }
    return 0;
}

B - 圆与三角形

给出圆的圆心和半径，以及三角形的三个顶点，问圆同三角形是否相交。相交输出"Yes"，否则输出"No"。（三角形的面积大于0）。

• Input

第1行：一个数T，表示输入的测试数量(1 <= T <= 10000)，之后每4行用来描述一组测试数据。 4-1：三个数，前两个数为圆心的坐标xc, yc，第3个数为圆的半径R。(-3000 <= xc, yc <= 3000, 1 <= R <= 3000） 4-2：2个数，三角形第1个点的坐标。 4-3：2个数，三角形第2个点的坐标。 4-4：2个数，三角形第3个点的坐标。(-3000 <= xi, yi <= 3000）

• Output

共T行，对于每组输入数据，相交输出"Yes"，否则输出"No"。

• Sample Input

2
0 0 10
10 0
15 0
15 5
0 0 10
0 0
5 0
5 5

• Sample Output

Yes
No

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
 
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=1e6+500;
const int M=1e4+5;
const ll INF=0x3f3f3f3f;
const int mod=1e9+7;
const double EPS = 1e-9;
const double PI = acos(-1.0);
 
struct Node{
    double x;
    double y;
};
 
double dis(Node a,Node b){//计算两点之间距离
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
 
int disline(Node a,Node b,Node c,double R){//判断在圆外的两点形成的线段是否与圆相交
    if(c.x==b.x){//bc线段与x轴垂直
        if(abs(a.x-b.x)>R)//圆心到bc直线的距离大于半径则不相交
            return 0;
        else{//圆心到bc直线的距离小于半径
            if(b.y>a.y&&c.y>a.y || b.y<a.y&&c.y<a.y)//若两点y均大于（小于）圆心的y则不相交
                return 0;
            else//其余情况均相交
                return 1;
        }
    }
    else if(c.y==b.y){//bc线段与y轴垂直，原理同与x轴垂直
        if(abs(a.y-b.y)>R)
            return 0;
        else{
            if(b.x<a.x&&c.x<a.x || b.x>a.x&&c.x>a.x)
                return 0;
            else
                return 1;
        }
    }
    else{
        Node d;//bc直线上圆心r的垂点
        double kbc=(b.y-c.y)/(b.x-c.x);//根据公式y=kx+b,kbc为bc直线的k，bbc为其中的b，kad、bad同理
        double bbc=b.y-kbc*b.x;
        double kad=-1/kbc;
        double bad=a.y-kad*a.x;
        d.x=(bad-bbc)/(kbc-kad);
        d.y=kbc*d.x+bbc;
        if(dis(a,d)>R)//圆心到直线bc的距离大于半径则不相交
            return 0;
        else{//圆心到直线bc的距离小于半径
            if(d.x>b.x&&d.x>c.x || d.x<b.x&&d.x<c.x)//垂点d不在线段bc上则不相交
                return 0;
            else//其余情况则相交
                return 1;
        }
    }
 
}
 
int solve(Node r,Node t1,Node t2,Node t3,double R){
    if(dis(r,t1)<R && dis(r,t2)<R && dis(r,t3)<R)//三点均在圆内则圆与三角形不相交
        return 0;
    //三点均在圆外，圆与三条线段均不相交，则圆与三角形不相交
    if(dis(r,t1)>R && dis(r,t2)>R && dis(r,t3)>R && !disline(r,t1,t2,R) && !disline(r,t1,t3,R) && !disline(r,t2,t3,R))
        return 0;
    return 1;
}
int main(){
    int T;
    scanf("%d",&T);
    Node r,t1,t2,t3;
    double R;
    while(T--){
        scanf("%lf%lf%lf",&r.x,&r.y,&R);
        scanf("%lf%lf",&t1.x,&t1.y);
        scanf("%lf%lf",&t2.x,&t2.y);
        scanf("%lf%lf",&t3.x,&t3.y);
        if(solve(r,t1,t2,t3,R))
            printf("Yes\n");
        else
            puts("No");
    }
 
    return 0;
}

C - 球与射线

gameboy是一个CS高手，他最喜欢的就是扮演警察，手持M4爆土匪的头。也许这里有人没玩过CS，有必要介绍一下“爆头”这个术语：所谓爆头，就是子弹直接命中对方的头部，以秒杀敌人。

现在用一个三维的直角坐标系来描述游戏中的三维空间（水平面为xoy平面，z轴正方向是上方）。假设游戏中角色的头是一个标准的球。告诉你土匪的身高，头部半径，所站位置的坐标；gameboy所控警察的身高，头部半径，所站位置的坐标，以及枪头所指方向的单位向量。gameboy所控警察所握的是M4，抢瞄准时枪膛中的子弹跟视线基本同线，我们忽略它们的距离，就当成同线。由于土匪手持AK47,所以他是很嚣张地正立着。而警察手持M4，正在瞄准，由于瞄准时身体微弯，视线从头心出发，他头部的实际高度比正立时低10%。

你的任务就是，计算gameboy在这一刻扣下扳机，能否爆土匪的头。注意：这里忽略子弹的直径和重力作用，也就是说子弹是无限小的，弹道是一条笔直的射线，警察与土匪间没有障碍物。并且只要子弹擦到头部，哪怕是边缘，也算爆头。

• Input

测试数据的第一行有一个正整数T，表示有T组测试数据。每组数据的第一行有五个实数，h1,r1,x1,y1,z1，分别表示土匪的身高，头部半径以及所站的位置。第二行有八个实数，h2,r2,x2,y2,z2,x3,y3,z3，分别表示警察的身高，头部半径，所站位置，以及枪头所指方向的方向向量。

• Output

每一组输入数据对应一行输出。如果能爆土匪的头，输出"YES",否则输出"NO"。

• Sample Input

2
1.62 0.1 10.0 10.0 10.0
1.80 0.09 0.0 0.0 0.0 1.0 1.0 1.0
1.62 0.1 0.0 0.0 0.0
1.80 0.09 10.0 10.0 10.0 -1.0 -1.0 -1.0

• Sample Output

YES
YES

#include 
#include 
#include 
#include 
#include 
using namespace std;
#define eps 1e-8
#define inf 1e8
#define zero(x) (((x)>0?(x):-(X))
struct point3
{
    double x;
    double y;
    double z;
}temp,temp1,temp3;
struct line3
{
    point3 a;
    point3 b;
};
struct plane3
{
    point3 a;
    point3 b;
    point3 c;
    double r;
};
point3 xmult(point3 u,point3 v)
{
    point3 ret;
    ret.x=u.y*v.z-v.y*u.z;
    ret.y=u.z*v.x-u.x*v.z;
    ret.z=u.x*v.y-u.y*v.x;
    return ret;
}
double dis(point3 a,point3 b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}
double vlen(point3 p)
{
    return sqrt(p.x*p.x+p.y*p.y+p.z*p.z);
}
double dmult(point3 u,point3 v)
{
    return u.x*v.x+u.y*v.y+u.z*v.z;
}
point3 subt(point3 u,point3 v)
{
    point3 ret;
    ret.x=u.x-v.x;
    ret.y=u.y-v.y;
    ret.z=u.z-v.z;
    return ret;
}
double linetoline(line3 u,line3 v)
{
    point3 n=xmult(subt(u.a,u.b),subt(v.a,v.b));
    return fabs(dmult(subt(u.a,v.a),n))/vlen(n);
}
double angle_cos(line3 u,line3 v)
{
    return dmult(subt(u.a,u.b),subt(v.a,v.b))/vlen(subt(u.a,u.b))/vlen(subt(v.a,v.b));
}
double ptoline(point3 p,line3 l)
{
    return vlen(xmult(subt(p,l.a),subt(l.b,l.a)))/dis(l.a,l.b);
}
int main()
{
    int t;
    point3 pos1,pos2,dir,head1,head2,dir1,dir2;
    double h1,r1,h2,r2,angle,d;
    line3 a,b;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lf%lf%lf%lf%lf",&h1,&r1,&pos1.x,&pos1.y,&pos1.z);
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&h2,&r2,&pos2.x,&pos2.y,&pos2.z,&dir.x,&dir.y,&dir.z);
        head1=pos1;
        head1.z+=(h1-r1);
        head2=pos2;
        head2.z+=(h2*0.9-r2);
        a.a=head2;//警察-》土匪
        a.b=head1;
        b.a=head2;
        b.b=dir;
        b.b.x+=b.a.x;
        b.b.y+=b.a.y;
        b.b.z+=b.a.z;
        angle=angle_cos(a,b);
        if(angle <= -eps)
        {
            printf("NO\n");
            continue;
        }
        d=ptoline(head1,b);
        if(d <= r1)
        printf("YES\n");
        else
        printf("NO\n");
    }
    return 0;
}

D - 球与立方体(较难)

In physical simulations, video games and computational geometry, collision detection involves algorithms for checking for collision, i.e. intersection, of two given objects. Collision detection algorithms are a basic component of 3D video games. Without them, characters could go through walls and other obstacles.
Here comes an interesting problem, given a ball and a cuboid, you need to detect whether they collide. We say that two objects collide if and only if they share at least one point.

• Input

  The first line of input is the number of test cases.
  Each test case contains two lines, the first line contains 24 integers X1, Y1, Z1, …, X8, Y8, Z8, representing the 8 vertexes of the cuboid. Vertexes are given in random order and you can make sure that all edges of the cuboid are parallel to coordinate axes; the second line contains 4 integers X,Y,Z,R representing the central point of the ball and its radius. All integers given are non-negative and will be less than 100000.

• Output

  For each case output “Yes” Or “No” on a single line.

• Sample Input

2
0 0 0 0 0 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 1
2 2 2 2
0 0 0 0 0 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 1
2 2 2 1

• Sample Output

Yes
No

#include 
#include 
using namespace std;
 
struct Pt {
    int x, y, z;
};
 
bool operator < (Pt a, Pt b) {
    return a.x + a.y + a.z < b.x + b.y + b.z;
}
 
long long delta(int lower, int upper, int p) {
    if (p < lower) return lower - p;
    if (p > upper) return p - upper;
    return 0;
}
 
int main() {
    int cs;
    scanf("%d", &cs);
    while (cs--) {
        int xb, yb, zb, r;
        Pt v[8];
        for (int i = 0; i < 8; i++) scanf("%d%d%d", &v[i].x, &v[i].y, &v[i].z);
        scanf("%lld%lld%lld%lld", &xb, &yb, &zb, &r);
        sort(v, v + 8);
        long long dx = delta(v[0].x, v[7].x, xb);
        long long dy = delta(v[0].y, v[7].y, yb);
        long long dz = delta(v[0].z, v[7].z, zb);
        if (dx * dx + dy * dy + dz * dz <= (long long)r * r) {
            printf("Yes\n");
        } else {
            printf("No\n");
        }
    }
    return 0;
}

E - 三角形与观察体

Long long ago, there was a world of triangles. A smart guy in that world invented a camera, whose viewfinder was a
triangle. The camera’s visual range could be represented by three RAYS. As the figure shows, the camera’s visual
range could be represented by three rays OA, OB, OC. Note that the visual range is INFINITE.

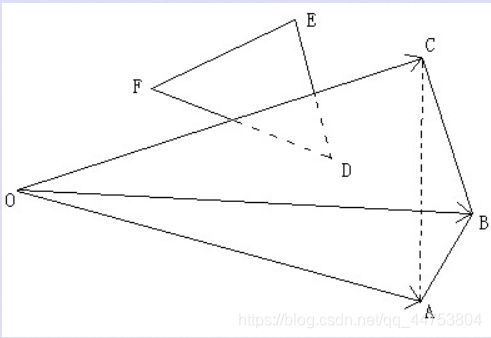
Now, we have a camera with known visual range and a triangle DEF in the space. The inventor wants to know if the
camera can see the triangle, in other words, if there is at least one point of the triangle strict in the visual range.

• Input

The input consists of multiple test cases. The first line of input contains an integer T, which is the number of test cases.

The first line of each test case contains 12 integers: Ox, Oy, Oz, Ax, Ay, Az, Bx, By, Bz, Cx, Cy, Cz. The second line
contains 9 integers: Dx, Dy, Dz, Ex, Ey, Ez, Fx, Fy, Fz.
All the integers in a line are separated by a whitespace.

[Technical Specification]
T is an integer, and T <= 1000.
The input guaranteed that if you look from O, three points ABC are always arranged counterclockwise.
All integers EXCEPT T is in the range of [-100,100].
We guarantee the camera and the triangle are not degenerate.

• Output

For each test case, display a single line contains the result, “YES” for visible, “NO” for not visible.

• Sample Input

2
90 -14 -17 71 98 94 69 59 -16 -52 68 13
-69 -96 43 81 -67 -79 66 -51 -53
0 0 1 0 0 0 1 0 0 0 1 0
0 0 -5 0 0 -6 1 1 -6

• Sample Output

NO
YES

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner cin = new Scanner(System.in);
		int t = cin.nextInt();
		double box[][][] = new double[t][4][3];
		double point[][][] = new double[t][3][3];
		for (int k = 0; k < t; k++) {
			for (int i = 0; i < 4; i++) {
				for (int j = 0; j < 3; j++) {
					box[k][i][j] = cin.nextDouble();
				}
			}
			
			for (int ii = 0; ii < 3; ii++) {
				for (int jj = 0; jj < 3; jj++) {
					point[k][ii][jj] = cin.nextDouble();
				}
			}

		}
		for (int i = 0; i < t; i++) {
			boolean flag=false;
			flag=inOrOut(box[i],point[i]);
			for(int j=0;j<2000;j++) {
				if(flag)break;
				else{
					vision(box[i],0.1);//每次延长视野0.1
					flag=inOrOut(box[i],point[i]);//当三角形完全大于视野切面 
				}
			}
			if(flag) {
				System.out.println("YES");
			}//当视野与三角形 有交点
		    else if (pointInTetrahedron(point[i][0], box[i]) || pointInTetrahedron(point[i][1], box[i])
					|| pointInTetrahedron(point[i][2], box[i])) {
				System.out.println("YES");
			} else
				System.out.println("NO");
		}

	}
    public static boolean inOrOut(double [][]pointa,double [][]pointb) {//当视野三个顶点都在三角形内
    	boolean flag=false;
     double s=area(distance(pointb[0],pointb[1]),distance(pointb[0],pointb[2]),distance(pointb[2],pointb[1]));
     for(int i=1;i<4;i++) {
    	 double s1= area(distance(pointa[i],pointb[0]),distance(pointa[i],pointb[1]), distance(pointb[0],pointb[1]));
    	 double s2=area(distance(pointa[i],pointb[1]), distance(pointa[i],pointb[2]),distance(pointb[1],pointb[2]));
    	 double s3=area( distance(pointa[i],pointb[0]),distance(pointa[i],pointb[2]), distance(pointb[0],pointb[2]));
    	 flag=acreage(s1,s2,s3,s);
    	 if(flag)break;
     }
     return flag;
    }
	public static double distance(double []pointx,double []pointy) {
		
		double number0=(pointx[0]-pointy[0])*(pointx[0]-pointy[0]);
		double number1=(pointx[1]-pointy[1])*(pointx[1]-pointy[1]);
		double number2=(pointx[2]-pointy[2])*(pointx[2]-pointy[2]);
		return Math.sqrt(number0+number1+number2);
	}
	public static double area(double a,double b ,double c) {
		double p=(a+b+c)/2;
		return Math.sqrt(p*(p-a)*(p-b)*(p-c));
	}
	public static boolean acreage(double s1,double s2,double s3,double s) {
		if((s1+s2+s3)==s) {
			return true;
		}
		return false;
		
	}
	public static void vision(double[][] box,double increment) {
		// 将视野扩大化
		double number[] = new double[3];
		int flag[] = new int[3];
		for (int i = 1; i < 4; i++) {
			flag[i-1]=0;
			if (box[i][0] > box[0][0]) {
				number[i - 1] = box[i][0];
				box[i][0] = box[i][0] + increment;
			} else if (box[i][0] < box[0][0]) {
				number[i - 1] = box[i][0];
				box[i][0] = box[i][0] - increment;
			} else {
				flag[i-1]=1;
				if (box[i][1] > box[0][1]) {
					number[i - 1] = box[i][1];
					box[i][1] = box[i][1] + increment;
				} else if (box[i][1] < box[0][1]) {
					number[i - 1] = box[i][1];
					box[i][1] = box[i][1] - increment;
				} else {
					flag[i-1]=2;
					if (box[i][2] > box[0][2]) {
						number[i - 1] = box[i][2];
						box[i][2] = box[i][2] + increment;
					} else if (box[i][2] < box[0][2]) {
						number[i - 1] = box[i][2];
						box[i][2] = box[i][2] - increment;
					}else {
						number[i - 1] = box[i][2];
						box[i][2] = box[i][2];
					}
					
				}
			}
		}
		for (int i = 1; i < 4; i++) {
			if (flag[i - 1] == 0) {
				box[i][1] = (box[i][1] - box[0][1]) * (box[i][0] - box[0][0]) / (number[i - 1] - box[0][0]) + box[0][1];
				box[i][2] = (box[i][2] - box[0][2]) * (box[i][0] - box[0][0]) / (number[i - 1] - box[0][0]) + box[0][2];
			}
			if (flag[i - 1] == 1) {
				box[i][0] = (box[i][0] - box[0][0]) * (box[i][1] - box[0][1]) / (number[i - 1] - box[0][1]) + box[0][0];
				box[i][2] = (box[i][2] - box[0][2]) * (box[i][1] - box[0][1]) / (number[i - 1] - box[0][1]) + box[0][2];
			} else {
				box[i][0] = (box[i][0] - box[0][0]) * (box[i][2] - box[0][2]) / (number[i - 1] - box[0][2]) + box[0][0];
				box[i][1] = (box[i][1] - box[0][1]) * (box[i][2] - box[0][2]) / (number[i - 1] - box[0][2]) + box[0][1];
			}

		}
	}

	public static boolean pointInTetrahedron(double[] point, double[][] box) {
		// 标志点是否在四面体内
		boolean flag = true;
		// 扩展四面体矩阵，最后增加一列，数值全为1
		double[][] ts = new double[4][4];
		for (int j = 0; j < ts.length; j++) {
			for (int j2 = 0; j2 < ts.length - 1; j2++) {
				ts[j][j2] = box[j][j2];
			}
			ts[j][3] = 1;
		}
		// 用点的坐标分别替换四面体的点坐标，得到新的矩阵
		for (int i = 0; i < ts.length; i++) {
			// 数组的深度拷贝
			// 注意：对于一维数组可以直接使用clone()进行复制，
			// 但是对于二维数组必须对每一行进行深度复制才行
			double[][] ti = new double[ts.length][ts[0].length];
			for (int j = 0; j < ts.length; j++) {
				ti[j] = ts[j].clone();
			}
			// 点坐标替换四面体的点坐标
			ti[i][0] = point[0];
			ti[i][1] = point[1];
			ti[i][2] = point[2];
			// 如果点坐标替换之后的矩阵与原四面体矩阵两者符号不同，P点不在四面体内
			if (GetLineTran(ts, 4) * GetLineTran(ti, 4) < 0) {
				flag = false;
				break;
			}
		}
		return flag;
	}

	public static double GetLineTran(double[][] p, int n) { // 计算行列式的值
		if (n == 1)
			return p[0][0];

		double exChange = 1.0; // 记录行列式中交换的次数
		boolean isZero = false; // 标记行列式某一行的最右边一个元素是否为零

		for (int i = 0; i < n; i++) {// i 表示行号
			if (p[i][n - 1] != 0) { // 若第 i 行最右边的元素不为零
				isZero = true;

				if (i != (n - 1)) { // 若第 i 行不是行列式的最后一行
					for (int j = 0; j < n; j++) { // 以此交换第 i 行与第 n-1 行各元素
						double temp = p[i][j];
						p[i][j] = p[n - 1][j];
						p[n - 1][j] = temp;

						exChange *= -1.0;
					}
				}

				break;
			}
		}

		if (!isZero)
			return 0; // 行列式最右边一列元素都为零，则行列式为零。

		for (int i = 0; i < (n - 1); i++) {
			// 用第 n-1 行的各元素，将第 i 行最右边元素 p[i][n-1] 变换为 0，
			// 注意：i 从 0 到 n-2，第 n-1 行的最右边元素不用变换
			if (p[i][n - 1] != 0) {
				// 计算第 n-1 行将第 i 行最右边元素 p[i][n-1] 变换为 0的比例
				double proportion = p[i][n - 1] / p[n - 1][n - 1];

				for (int j = 0; j < n; j++) {
					p[i][j] += p[n - 1][j] * (-proportion);
				}
			}
		}

		return exChange * p[n - 1][n - 1] * GetLineTran(p, (n - 1));
	}
}

F - 多边形面积

“ 改革春风吹满地,
不会AC没关系;
实在不行回老家，
还有一亩三分地。
谢谢!（乐队奏乐）”

话说部分学生心态极好，每天就知道游戏，这次考试如此简单的题目，也是云里雾里，而且，还竟然来这么几句打油诗。
好呀，老师的责任就是帮你解决问题，既然想种田，那就分你一块。
这块田位于浙江省温州市苍南县灵溪镇林家铺子村，多边形形状的一块地，原本是linle 的，现在就准备送给你了。不过，任何事情都没有那么简单，你必须首先告诉我这块地到底有多少面积，如果回答正确才能真正得到这块地。
发愁了吧？就是要让你知道，种地也是需要AC知识的！以后还是好好练吧…

• Input

输入数据包含多个测试实例，每个测试实例占一行，每行的开始是一个整数n(3<=n<=100)，它表示多边形的边数（当然也是顶点数），然后是按照逆时针顺序给出的n个顶点的坐标（x1, y1, x2, y2… xn, yn）,为了简化问题，这里的所有坐标都用整数表示。
输入数据中所有的整数都在32位整数范围内，n=0表示数据的结束，不做处理。

• Output

对于每个测试实例，请输出对应的多边形面积，结果精确到小数点后一位小数。
每个实例的输出占一行。

• Sample Input

3 0 0 1 0 0 1
4 1 0 0 1 -1 0 0 -1
0

• Sample Output

0.5
2.0

#include
#include
using namespace std;
#define maxn 101
typedef struct point
{
      int x[maxn];
      int y[maxn];
};
int main()
{
      point dian;
      int n, x1, x2,x3, y1, y2, y3;
      double S;
      while (cin>>n&&n)
      {
             S = 0;
             for (int i = 0; i <n; i++)
             {
                   cin >> dian.x[i]>> dian.y[i];
             }
             x1=dian.x[0];//固定点x坐标
             y1=dian.y[0];//固定点y坐标
             for (int i =1; i <n-1; i++)
             {
                   x2 = dian.x[i];
                   y2 = dian.y[i];
                   x3 = dian.x[i+1];
                   y3 = dian.y[i+1];
                   S += (double)(x2*y3 + x1*y2 +x3*y1 - x3*y2 - x2*y1 - x1*y3) / 2.0;
             }
             printf("%.1lf\n",S);//注意输出
      }
      return 0;
}

G - 利用凸包计算点集直径

Bessie, Farmer John’s prize cow, has just won first place in a bovine beauty contest, earning the title ‘Miss Cow World’. As a result, Bessie will make a tour of N (2 <= N <= 50,000) farms around the world in order to spread goodwill between farmers and their cows. For simplicity, the world will be represented as a two-dimensional plane, where each farm is located at a pair of integer coordinates (x,y), each having a value in the range -10,000 … 10,000. No two farms share the same pair of coordinates.

Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms.

• Input

• Line 1: A single integer, N

• Lines 2…N+1: Two space-separated integers x and y specifying coordinate of each farm

• Output

• Line 1: A single integer that is the squared distance between the pair of farms that are farthest apart from each other.

• Sample Input

4
0 0
0 1
1 1
1 0

• Sample Output

2
Hint
Farm 1 (0, 0) and farm 3 (1, 1) have the longest distance (square root of 2)

#include 
#include 
#include 
#include 
using namespace std;

struct Point
{
    int x,y;
    Point(int _x = 0, int _y = 0)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x, y - b.y);
    }
    int operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    int operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input()
    {
        scanf("%d%d",&x,&y);
    }
};
int dist2(Point a,Point b)
{
    return (a-b)*(a-b);
}
const int MAXN = 50010;
Point list[MAXN];
int Stack[MAXN],top;
bool _cmp(Point p1,Point p2)
{
    int tmp = (p1-list[0])^(p2-list[0]);
    if(tmp > 0)return true;
    else if(tmp == 0 && dist2(p1,list[0]) <= dist2(p2,list[0]))
        return true;
    else return false;
}
void Graham(int n)
{
    Point p0;
    int k = 0;
    p0 = list[0];
    for(int i = 1;i < n;i++)
        if(p0.y > list[i].y || (p0.y == list[i].y && p0.x > list[i].x))
        {
            p0 = list[i];
            k = i;
        }
    swap(list[0],list[k]);
    sort(list+1,list+n,_cmp);
    if(n == 1)
    {
        top = 1;
        Stack[0] = 0;
        return;
    }
    if(n == 2)
    {
        top = 2;
        Stack[0] = 0;
        Stack[1] = 1;
        return;
    }
    Stack[0] = 0;
    Stack[1] = 1;
    top = 2;
    for(int i = 2;i < n;i++)
    {
        while(top > 1 && ((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]])) <= 0 )
            top--;
        Stack[top++] = i;
    }
}
//旋转卡壳，求两点间距离平方的最大值
int rotating_calipers(Point p[],int n)
{
    int ans = 0;
    Point v;
    int cur = 1;
    for(int i = 0;i < n;i++)
    {
        v = p[i]-p[(i+1)%n];
        while((v^(p[(cur+1)%n]-p[cur])) < 0)
            cur = (cur+1)%n;
        //printf("%d %d\n",i,cur);
        ans = max(ans,max(dist2(p[i],p[cur]),dist2(p[(i+1)%n],p[(cur+1)%n])));
    }
    return ans;
}
Point p[MAXN];
int main()
{
    int n;
    while(scanf("%d",&n) == 1)
    {
        for(int i = 0;i < n;i++)
            list[i].input();
        Graham(n);
        for(int i = 0;i < top;i++)
            p[i] = list[Stack[i]];
        printf("%d\n",rotating_calipers(p,top));
    }
    return 0;
}

H - 利用凸包求面积最大三角形

Given n distinct points on a plane, your task is to find the triangle that have the maximum area, whose vertices are from the given points.
Input
The input consists of several test cases. The first line of each test case contains an integer n, indicating the number of points on the plane. Each of the following n lines contains two integer xi and yi, indicating the ith points. The last line of the input is an integer −1, indicating the end of input, which should not be processed. You may assume that 1 <= n <= 50000 and −104 <= xi, yi <= 104 for all i = 1 . . . n.
Output
For each test case, print a line containing the maximum area, which contains two digits after the decimal point. You may assume that there is always an answer which is greater than zero.
Sample Input
3
3 4
2 6
2 7
5
2 6
3 9
2 0
8 0
6 5
-1
Sample Output
0.50
27.00

#include 
#include 
#include 
#include 
#include 
using namespace std;

struct Point
{
    int x,y;
    Point(int _x = 0, int _y = 0)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x, y - b.y);
    }
    int operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    int operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input()
    {
        scanf("%d%d",&x,&y);
    }
};
int dist2(Point a,Point b)
{
    return (a-b)*(a-b);
}
const int MAXN = 50010;
Point list[MAXN];
int Stack[MAXN],top;
bool _cmp(Point p1,Point p2)
{
    int tmp = (p1-list[0])^(p2-list[0]);
    if(tmp > 0)return true;
    else if(tmp == 0 && dist2(p1,list[0]) <= dist2(p2,list[0]))
        return true;
    else return false;
}
void Graham(int n)
{
    Point p0;
    int k = 0;
    p0 = list[0];
    for(int i = 1;i < n;i++)
        if(p0.y > list[i].y || (p0.y == list[i].y && p0.x > list[i].x))
        {
            p0 = list[i];
            k = i;
        }
    swap(list[0],list[k]);
    sort(list+1,list+n,_cmp);
    if(n == 1)
    {
        top = 1;
        Stack[0] = 0;
        return;
    }
    if(n == 2)
    {
        top = 2;
        Stack[0] = 0;
        Stack[1] = 1;
        return;
    }
    Stack[0] = 0;
    Stack[1] = 1;
    top = 2;
    for(int i = 2;i < n;i++)
    {
        while(top > 1 && ((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]])) <= 0 )
            top--;
        Stack[top++] = i;
    }
}
//旋转卡壳，求两点间距离平方的最大值
int rotating_calipers(Point p[],int n)
{
    int ans = 0;
    Point v;
    int cur = 1;
    for(int i = 0;i < n;i++)
    {
        int j = (i+1)%n;
        int k = (j+1)%n;
        while(j != i && k != i)
        {
            ans = max(ans,abs((p[j]-p[i])^(p[k]-p[i])) );
            while( ( (p[i]-p[j])^(p[(k+1)%n]-p[k]) ) < 0 )
                k = (k+1)%n;
            j = (j+1)%n;
        }
    }
    return ans;
}
Point p[MAXN];
int main()
{
    int n;
    while(scanf("%d",&n) == 1)
    {
        if(n == -1)break;
        for(int i = 0;i < n;i++)
            list[i].input();
        Graham(n);
        for(int i = 0;i < top;i++)
            p[i] = list[Stack[i]];
        int ans = rotating_calipers(p,top);
        printf("%.2lf\n",ans/2.0);
    }
    return 0;
}

I - 多边形重心(较难)

There are many secret openings in the floor which are covered by a big heavy stone. When the stone is lifted up, a special mechanism detects this and activates poisoned arrows that are shot near the opening. The only possibility is to lift the stone very slowly and carefully. The ACM team must connect a rope to the stone and then lift it using a pulley. Moreover, the stone must be lifted all at once; no side can rise before another. So it is very important to find the centre of gravity and connect the rope exactly to that point. The stone has a polygonal shape and its height is the same throughout the whole polygonal area. Your task is to find the centre of gravity for the given polygon.
Input
The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing a single integer N (3 <= N <= 1000000) indicating the number of points that form the polygon. This is followed by N lines, each containing two integers Xi and Yi (|Xi|, |Yi| <= 20000). These numbers are the coordinates of the i-th point. When we connect the points in the given order, we get a polygon. You may assume that the edges never touch each other (except the neighboring ones) and that they never cross. The area of the polygon is never zero, i.e. it cannot collapse into a single line.
Output
Print exactly one line for each test case. The line should contain exactly two numbers separated by one space. These numbers are the coordinates of the centre of gravity. Round the coordinates to the nearest number with exactly two digits after the decimal point (0.005 rounds up to 0.01). Note that the centre of gravity may be outside the polygon, if its shape is not convex. If there is such a case in the input data, print the centre anyway.
Sample Input
2
4
5 0
0 5
-5 0
0 -5
4
1 1
11 1
11 11
1 11
Sample Output
0.00 0.00
6.00 6.00

```cpp
#include 
struct Point
{
    double x, y;
}P[1000001];
double Cross(Point a, Point b)//叉乘
{
    return (a.x*b.y - a.y*b.x);
}
Point FuncAdd(Point i, Point j)
{
    Point a;
    a.x = i.x + j.x;
    a.y = i.y + j.y;
    return a;
}
Point FuncMultiply(Point i, double j)//乘法
{
    Point a;
    a.x = i.x*j;
    a.y = i.y*j;
    return a;
}
int main()
{
    int T;
    long long N, i;
    double TotalArea, R_x, R_y;
    Point Sigma, temp;
    scanf("%d", &T);
    while (T--)
    {
        scanf("%lld", &N);
        scanf("%lf%lf", &P[1].x, &P[1].y);
        TotalArea = 0;
        Sigma = { 0,0 };
        for (i = 2; i <= N; i++)
        {
            scanf("%lf%lf", &P[i].x, &P[i].y);
            TotalArea += Cross(P[i], P[i - 1]);
            temp = FuncMultiply(FuncAdd(P[i], P[i - 1]), Cross(P[i], P[i - 1]));
            Sigma.x += temp.x;
            Sigma.y += temp.y;
        }
        TotalArea += Cross(P[1], P[N]);
        temp = FuncMultiply(FuncAdd(P[1], P[N]), Cross(P[1], P[N]));
        Sigma.x += temp.x;
        Sigma.y += temp.y;
        R_x = Sigma.x / TotalArea / 3;
        R_y = Sigma.y / TotalArea / 3;
        if (R_x == -0)R_x = 0;
        if (R_y == -0)R_y = 0;
        printf("%.2lf %.2lf\n", R_x, R_y);
    }
}

J - 最小面积三角形(较难)

Little John is herding his father’s cattles. As a lazy boy, he cannot tolerate chasing the cattles all the time to avoid unnecessary omission. Luckily, he notice that there were N trees in the meadow numbered from 1 to N, and calculated their cartesian coordinates (Xi, Yi). To herding his cattles safely, the easiest way is to connect some of the trees (with different numbers, of course) with fences, and the close region they formed would be herding area. Little John wants the area of this region to be as small as possible, and it could not be zero, of course.
Input
The first line contains the number of test cases T( T<=25 ). Following lines are the scenarios of each test case.
The first line of each test case contains one integer N( 1<=N<=100 ). The following N lines describe the coordinates of the trees. Each of these lines will contain two float numbers Xi and Yi( -1000<=Xi, Yi<=1000 ) representing the coordinates of the corresponding tree. The coordinates of the trees will not coincide with each other.
Output
For each test case, please output one number rounded to 2 digits after the decimal point representing the area of the smallest region. Or output “Impossible”(without quotations), if it do not exists such a region.
Sample Input
1
4
-1.00 0.00
0.00 -3.00
2.00 0.00
2.00 2.00
Sample Output
2.00

#include 
#include 
#include 
using namespace std;
struct point
{
    double x,y;
}p[103];//构造点
 
double area(point p1,point p2,point p3)
{
    return abs(p1.x*p2.y+p1.y*p3.x+p2.x*p3.y-p2.y*p3.x-p1.x*p3.y-p1.y*p2.x)/2.0;
}//计算三角形的面积
 
int main()
{
    int t,n;
    cin>>t;
    for(int ni=1;ni<=t;ni++)
    {
        cin>>n;
        for(int i=1;i<=n;i++)
            cin>>p[i].x>>p[i].y;
        int flag=0;
        double Min=9999999;//用于最后输出
        for(int i=1;i<=n;i++)//枚举三个不同的点，三重循环完成
        {
            for(int j=i+1;j<=n;j++)
            {
                for(int k=j+1;k<=n;k++)
                {
                    double temp=area(p[i],p[j],p[k]);
 
                        if(temp<Min&&temp!=0)//temp不为0才能构成三角形
                        {
                            Min=temp;
                            flag=1;
                        }
                }
            }
        }
        if(flag)
            cout<<setiosflags(ios::fixed)<<setprecision(2)<<Min<<endl;
        else
            cout<<"Impossible"<<endl;
    }
    return 0;
}

K - 又一个线段相交(较难)

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.

Input
Input consists of a number of cases. The data for each case start with 1 ≤ n ≤ 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.
Sample Input
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0
Sample Output
Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

#include 
#include 
#include 
#include 
#include 
using namespace std;
struct point
{
    double x,y;
};
struct line
{
    point p1,p2;
} a[100010];
double chacheng (struct point p1,struct point p2,point p3)
{
    return (p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x);
}
int judge(struct line l1,struct line l2)
{
    if( min(l2.p1.x,l2.p2.x)<=max(l1.p1.x,l1.p2.x)&&min(l2.p1.y,l2.p2.y)<=max(l1.p1.y,l1.p2.y)&&min(l1.p1.x,l1.p2.x)<=max(l2.p1.x,l2.p2.x) &&min(l1.p1.y,l1.p2.y)<=max(l2.p1.y,l2.p2.y)
            &&chacheng(l1.p1,l2.p2,l2.p1)*chacheng(l1.p2,l2.p2,l2.p1)<=0 &&chacheng(l2.p1,l1.p2,l1.p1)*chacheng(l2.p2,l1.p2,l1.p1)<=0 )
        return 1;
    else
        return 0;
}
int main()
{
    int n,i,j;
    int flag[100010];
    while(~scanf("%d",&n))
    {
        if(n==0)
            break;
        for(i=0; i<n; i++)
            scanf("%lf %lf %lf %lf",&a[i].p1.x,&a[i].p1.y,&a[i].p2.x,&a[i].p2.y);
        memset(flag,0,sizeof(flag));
        for(i=0; i<n-1; i++)
            for(j=i+1; j<n; j++)
                if(judge(a[i],a[j]))
                {
                    flag[i]=1;
                    break;
                }
        printf("Top sticks: ");
        for(i=0; i<n; i++)
            if(flag[i]==0)
            {
                if(i==n-1)
                    printf("%d.\n",i+1);
                else
                    printf("%d, ",i+1);
            }
    }
    return 0;
}