对学习器的泛化性能进行比较的时候, 不仅需要有效可行的实验估计方法, 还要评估模型泛化能力的评价标准, 这就是性能度量(performance measure), 性能度量反映任务需求, 不同的性能度量往往导致不同的评判结果.
首先, 我们先来看看机器学习中常见的评价指标
回归任务的常见性能指标是均方误差(MSE, mean squared error)
\[E(f; D) = \frac{1}{m}\sum_i^m \left( f(x_i)-y_i\right)^2\]
\(f(x_i)\) 为预测结果, \(y_i\) 为真实标签, m 为样本个数, 数据集 D
下面介绍分类任务中常见的性能度量
错误率和准确率
错误率即适用于二分类也适用于多分类, 定义为分类错误的样本数占样本总数的比例, 准确率(Accuracy)则是分类正确的样本数占样本总数的比例
\[\bf Error(f; D) = \frac{1}{m}\sum_i^m \mathbb I \left( f(x_i) \ne y_i \right) \]
\[\bf Accuracy(f; D) = \frac{1}{m}\sum_i^m \mathbb I \left( f(x_i)=y_i \right) \]
查准率(精度)和查全率
错误率和准确率虽然常用, 但并不能满足所有的任务要求, 如信息检索中, 我们关心 "检索出的信息有多少是用户感兴趣的", "用户感兴趣的信息有多少被检索出来了", 查准率(Precision)和查全率(Recall)更适合此类需求的性能度量.
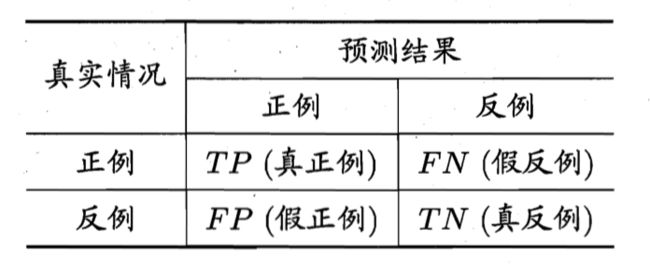
对于二分类问题, 可以将样例根据其真实类别和学习期的预测类别组合为如下四种情形
| 术语 | 含义 |
|---|---|
| True Positive | 被模型预测为正的正样本 |
| True Negative | 被模型预测为负的负样本 |
| False Negative | 被模型预测为负的正样本 |
| False Positive | 被模型预测为正的负样本 |
| True/False | 表示学习器预测结果的正确与否 |
| Positives/Negatives | 表示学习器预测结果 |
| 样本总数 | TP + TN + FP + FN |
在理解一个组合的含义时, 如: True Negative
- 第一个关键字: True, 表明模型预测正确
- 第二个关键字: Negative, 表示学习器将该样例预测为负例
学习器预测正确且预测为负样本, 即该样本为被模型预测为负的负样本
Accuracy, 准确率反映了分类器统对整个样本的判定能力——能将正的判定为正,负的判定为负
\[\bf Accuracy = \frac{TP + TN}{TP + TN + FP + FN}\]
Precision
查准率(Precision, 精度)是针对预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。
\[ \begin{align} \bf Precision = \frac{TP}{TP+FP} \tag{1}\\ \end{align} \]
Recall
召回率(Recall, 又称为 TPR)是针对原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。
\[ \begin{align} \bf Recall = \frac{TP}{TP+FN} \tag{2} \end{align} \]
Precision 和 Recall 两者的抽样方式不同:
Recall 的抽样是每次取同一标签中的一个样本, 如果预测正确就计一分
Precision 的抽样是每次取你已预测为同一类别的一个样本,如果预测正确就计一分。
这里一个关键点是: 召回率是从数据集的同一标签的样本抽样, 而准确率是从已经预测为同一类别的样本抽样。Recall 和 Precision 都可以只针对一个类别。
True Positive Rate(真正率, 真阳性, TPR), 含义是检测出来的真阳性样本数占所有真实阳性样本数的比例。
\[ \begin{align*} \bf TPR = \frac{\text{被预测为正的正样本结果数}}{\text{正样本实际数}} = \frac{TP}{TP+FN} \end{align*} \]
False Positive Rate (假正率, 假阳性 FPR), 含义是检测出来的假阳性样本数除以所有真实阴性样本数
\[ \begin{align*} \bf FPR = \frac{\text{被预测为正的负样本结果数}}{\text{负样本总数}} = \frac{FP}{TN+FP} \end{align*} \]
可以看出真阳性和假阳性的计算分母包含整个样本集 (TP+FN) + (TN+FP)
True Negative Rate(真负率 , TNR), 含义是检测出来的真阴性样本数占所有真阴性样本数的比例。
\[ \begin{align*} \bf TNR = \frac{\text{被预测为负的负样本结果数}}{\text{负样本总数}} = \frac{TN}{TN+FP} \end{align*} \]
False Negative Rate(假负率, FNR), 含义是检测出来的假阴性样本数占所有真阳性样本数的比例。
\[ \begin{align*} \bf FNR = \frac{\text{被预测为负的正样本结果数}}{\text{正样本总数}} = \frac{FN}{TN+FN} \end{align*} \]
查准率和查全率是一对矛盾的度量.
一般来说, 查准率高时, 查全率往往偏低, 而查全率高时, 查准率往往偏低.
例如, 如果希望将好瓜尽可能多的选出来, 则可以通过选瓜的数量来实现; 如果将所有西瓜都选上, 那么所有好瓜也必然被选上, 但是这样查准率就会较低; 若希望选出的好瓜比例尽可能的高, 那么只挑选最有把握的瓜, 但是这样难免会漏掉不少好瓜, 使得查全率低. 通常只有一些简单的任务中, 才可能使得查全率和查准率都很高.
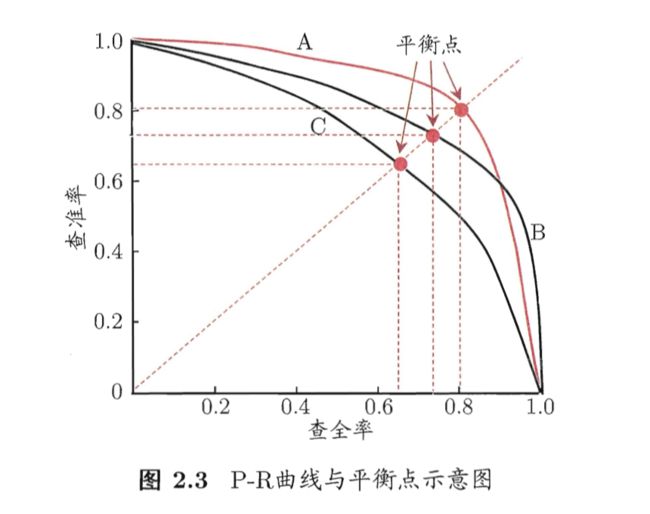
P-R 曲线
很多情形下, 我们可以根据学习器的预测结果对样例排序, 排在前面的是学习器认为"最可能"的正例的样本, 排在后面的是学习器认为"最不可能"是正例的样本. 按此顺序逐个将样本作为正例进行预测, 则每次计算当前的查准率和查全率.
以查准率为纵轴, 查全率为横轴作图, 就得到查准率-查全率曲线, 简称 "P-R曲线", 显示该曲线的图称为 "P-R图"
若一个 P-R 曲线被另一个 P-R 曲线 完全"包住"的话, 则后者的性能优于前者(面积越大, 性能越好吧).
ROC
ROC(receiver operating characteristic), 其显示的是分类器的真正率和假正率之间的关系
AUC(area under ROC curve), 即 ROC 曲线下方的面积
ROC与P-R关系
PR曲线和ROC曲线有什么联系和不同?
相同点: 首先从定义上PR曲线的R值是等于ROC曲线中的TPR值, 都是用来评价分类器的性能的。
不同点: ROC曲线是单调的而PR曲线不是(根据它能更方便调参), 可以用AUC的值得大小来评价分类器的好坏(是否可以用PR曲线围成面积大小来评价呢?), 正负样本的分布失衡的时候,ROC曲线保持不变,而PR曲线会产生很大的变化。
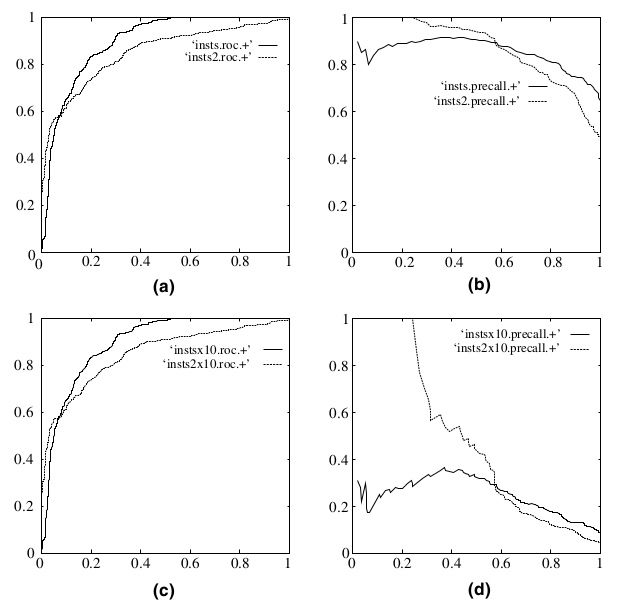
(a) (b) 分别是正反例相等的时候的ROC曲线和PR曲线
(c) (d) 分别是十倍反例一倍正例的ROC曲线和PR曲线
可以看出,在正负失衡的情况下,从ROC曲线看分类器的表现仍然较好(图c),然而从P-R曲线来看,分类器就表现的很差, 也就是说样本不均衡时, 使用 P-R 曲线更能区分不同分类器的性能.
事实情况是分类器确实表现的不好,是ROC曲线欺骗了我们(分析过程见知乎 qian lv 的回答)。
F-Score
F1_Score 是一种统计量, 定义为 Precision 和 Recall 加权调和平均,是IR(信息检索)领域的常用的一个评价标准,常用于评价分类模型的好坏. 由于 F-Score 综合了 Presion 和 Recall 的结果, 所以当 F-Score 较高时则能说明试验方法比较有效, 定义如下
\[{\displaystyle F_{1}=2 \cdot \left({\frac{1}{P}+\frac{1}{R}}\right)^{-1}=2\cdot {\frac {P \cdot R }{P +R }}}\]
在 F-Score 的通用定义如下,
\[ \begin{align*} F_\beta &= (1 + \beta^2) \cdot \left( \frac{1}{P} + \frac{\beta^2}{R} \right)^{-1} \\ &= (1 + \beta^2) \cdot \frac{P \cdot R}{(\beta^2 \cdot P) + R} \end{align*} \]
使用 \(β^2\), 只是为了说明 Precision 上的因子大于 0, 当 \(β^2 > 1\)时, 查全率有更大的影响, 当\(β^2 < 1\)时, 查准率有更大的影响
将式(1)和式(2)代入上式
\[{\displaystyle F_{\beta }={\frac {(1+\beta ^{2})\cdot TP }{(1+\beta ^{2})\cdot TP +\beta ^{2}\cdot FN +FP }}\,} \]
mean average precision
目标检测中衡量识别精度的指标是mAP(mean average precision)。多个类别物体检测中,每一个类别都可以根据recall和precision绘制一条曲线,AP就是该曲线下的面积,mAP是多个类别AP的平均值
为了更好地评估一个模型的准确率,人们提出的单个类别平均精度(AP),把准确率在recall值为Recall = {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1}时, 求平均值.
- Object-Detection-Metrics
- 目标检测模型的评估指标mAP详解(附代码)
Facebook开源的Detectron包含VOC数据集的mAP计算, 计算各个类别的AP值后,取平均值就可以得到最终的mAP值了。但是对于COCO数据集相对比较复杂,不过其提供了计算的API,感兴趣可以看一下cocodataset/cocoapi。