每日练习（实用C程序）

一、大数加法

关于大数问题，因为long,int等的范围有限，直接进行超大数字的运算会溢出。

常见的思路是将大整数字符串转化为数组，再用数组模拟大整数的运算。

具体而言，先将字符串中的数字字符顺序存入一个较大的整型数组，其元素代表整数的某一位或某几位(如万进制)；然后根据运算规则操作数组元素，以模拟整数运算；最后，将数组元素顺序输出。

数组方式操作方便，实现简单，缺点是空间利用率和执行效率不高。也可直接操作大整数字符串，从字符串末尾逆向计算。

由于数组要事先确定大小（数组的长度），但我们要计算的数字不确定。因此主要思想就是先用字符串输入保存在字符串数组中，再逆序存入整形数组进行最后逐位运算。

思路：输入采用字符数组保存，然后将输入存在整形数组里，然后逐位相加即可，同时注意进位处理。

参考：（https://blog.csdn.net/l_liangkk/article/details/51971158）

//大数加法
#include
#include
#define M 100005
char s1[M],s2[M];
int a[M],b[M],c[M];
int main()
{
    int i,j,k,n,m;
    while(scanf("%s%s",s1,s2))
    {
        memset(c,0,sizeof(c));
        memset(a,0,sizeof(a));memset(b,0,sizeof(b));
        n=strlen(s1);
        m=strlen(s2);
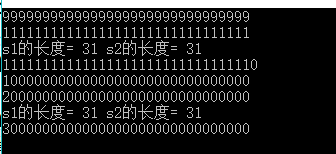
        printf("s1的长度= %d s2的长度= %d\n",n,m);
 /* 把字符串s1和s2逆序用数字排列*/
        for(i=0; im) k=n;
        else k=m;
        for(i=0; i<=k; i++)
        {
            c[i]+=a[i]+b[i];
            if(c[i]>9)
            {
                c[i+1]++;
                c[i]%=10;
            }
        }
        /*去除前导0*/
        i=k;
        while(c[i]==0) i--;
  /*判断两个非负数之和是否为0，以及逆序打印c[]*/
        if(i<0) printf("0");
        else
        {
            for(; i>=0; i--)
                printf("%d",c[i]);
        }
        printf("\n");
    }
    return 0;
}

二、大数乘方

乘方运算比如1^1=1,3^2=9 这种。

思路：先设定一个数组，并把数组初始化为0，并把这个数组最后一个元素初始化为1，然后把数组每一位乘以底数，再遍历数组，当元素大于10时，往前进位，循环这组操作直到达到指数次数

#include
#include
int main(){
	int *a,n,b;
	int i,j;
	a=(int *)malloc(sizeof(int) *200000); 
	for(i=0;i<200000;i++)
	a[i]=0;
	a[199999]=1;
	printf("请输入底数：\n");
	scanf("%d",&b);
	printf("请输入指数：\n");
	scanf("%d",&n);
	for(i=1;i=0;j--)
			if(a[j]>=10){//进位操作
				a[j-1]+=a[j]/10;
				a[j]%=10;
			}	
	}

		for(i=0;a[i]==0;i++);
		printf("乘方结果为：\n");
		for(;i<200000;i++)
		printf("%d",a[i]);
		printf("\n");
		free(a); 
}	

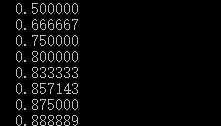
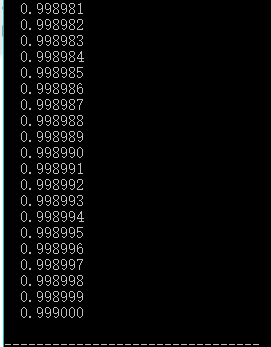
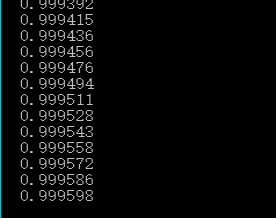
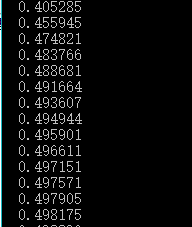
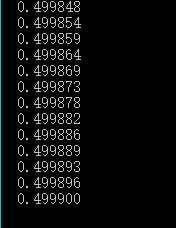
三、验证1/2，2/3，3/4,...........n/n+1  ....的极限是1

由运行结果得知随着n的增大，数列的值越来越接近1

#include
#include
void main(){
	float i;
	double sum1,sum2;
	for(i=1.0;i<1000;i++){
		sum2=i/(i+1.0);
		printf("  %f\n",sum2);
	}
}

四、验证函数极限  

 

 

#include
#include

void main(){
	int i;
	double sum1,sum2;
	double x,y;
	for(i=2;i<=64;i++){
		sum2=sin(3.14159265/i)/(3.14159265/i);
		printf("  %f\n",sum2);
	}
}

五、验证

#include
#include
void main(){
	int i;
	double sum1,sum2;
	double x,y;
	for(i=2;i<=64;i++){
		sum2=(1-cos(3.14159265/i))/((3.14159265/i)*(3.14159265/i));
		printf("  %f\n",sum2);
	}
}

六、验证是发散的

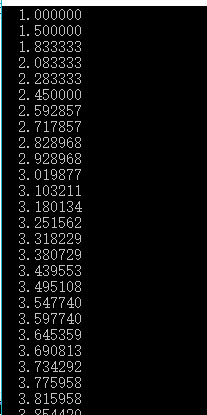
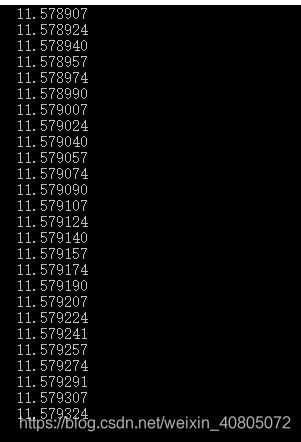
当然数学家已经证明了这个。在此通过计算机来，具体观察变化情况

从n=1到6000级数之和也没有停止增长

 

#include
#include
void main(){
	int i;
	double sum1=0.0;
	for(i=1;i<=60000;i++){
		sum1=sum1+(1.0/i);
		printf("  %f\n",sum1);
	}
}

七、验证

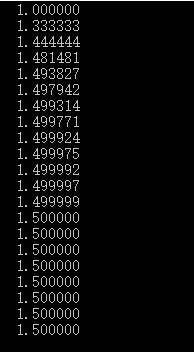
可看到随着n增大，级数之和稳定在1.5

#include
#include
void main(){
	int i;
	double sum1=0.0;
	for(i=0;i<=20;i++){
		sum1=sum1+1.0/(pow(3.0,i));
		printf("  %f\n",sum1);
	}
}

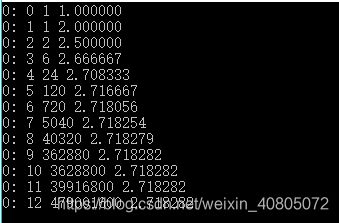
八、计算自然数e

在此用麦克劳林级数，

#include
#include
int fun(int);
void main(){
	int i;
	double sum1=0.0;
	for(i=0;i<=12;i++){
		sum1=sum1+(1.0/fun(i));
		printf("0: %d %d %f\n",i,fun(i),sum1);
	}
}
	int fun(int j){
		int sum;
		if(j==0)
		sum=1;
		else
		sum=j*fun(j-1);
		return(sum);
	}