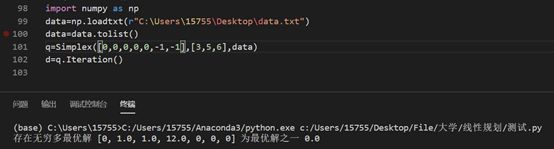
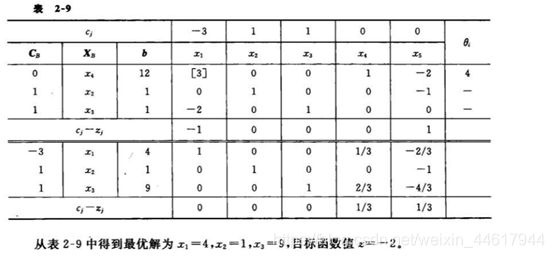
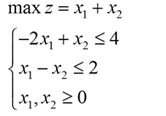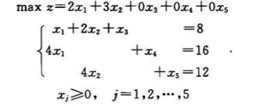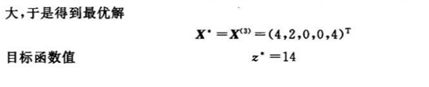单纯形算法及对偶的python实现

单纯形算法

使用python编程语言通过矩阵运算编程来实现单纯形算法。

1.建立模型后输入数据列出初始单纯形表

将线性规划问题转化为标准型，求minz转化为求max-z
以下图为例

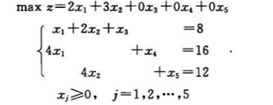
初始化

import numpy as np
class Simplex(object):
    #构造函数（初始化函数）
    def __init__(self,z,B,bound):  
        self.X_count=len(z)          #变量个数
        self.b_count=len(bound)      #约束条件个数
        self.z=z                     #目标函数
        self.C=[]                    #检验数
        self.B=B                     #基变量,由于运算规则必须按顺序给出基变量
        self.bound=bound             #约束条件,包括右端常数
        self.flag=0                  #解的类型，0为（暂时）无解，1为唯一最优解，2为无穷多最优解
        self.special=True            #无界解

2.进行最优性检验

计算所有的检验数，若所有的检验数都小于零，结束得到最优解，否则转下步。若检验数大于零而Pk<=0（θ无值可计算）,此问题属于无界解，结束，否则转入下一步。

    def Iteration(self):    	
        lim=100		#防止无限迭代
        while(lim>0):
            self.C=[] #检验数清空
            for j in range(self.X_count):     
                zj=0
                for i in range(self.b_count): #遍历第j列全行系数，计算第j个变量检验数
                    zj+=self.bound[i][j]*self.z[self.B[i]]#限制B基变量序号顺序之处
                self.C.append(self.z[j]-zj) #检验数,'cj-zj'
            self.Check() #判断迭代是否结束
            if self.flag>0: #有解，结束迭代
                break

单次迭代后对解的判断方法独立为Check()函数。
无可行解的情况出现在最后仍有人工变量非零，可在两阶段法的第一阶段确定。
特殊情况无界解的判定稍后分析。

    #Check()，检验是否为最优解且最优解是否唯一
    def Check(self):   	
        self.flag=1
        k=0
        for i in range(self.X_count):
            #检验数大于0，非最优解
            if self.C[i]>0:  
                self.flag=0
                break
            if abs(self.C[i])<0.00000001:   #计算存在误差
                k+=1
                #检验数中0的个数大于基变量个数，即存在非基变量检验数为零，则有无穷多最优解
                if k>self.b_count:
                    self.flag=2  

3.确定主元素，进行基变换

通过第二步我们计算出了所有的检验数。
找到最大检验数确定对应的换入变量。按照θ规则θi=min(bi/aik| aik>0) 确定换出变量。即能确定主元素。
在这里由于存在无界解这种特殊情况，该情况出现是因为在非基变量检验数大于0时theta无值可计算，非基变量系数小于零，即无约束。于是在FindMain()设计一个计数器，如果计数达到约束条件的行数，即theta全部为无穷大，设定special旗帜，则在最终输出时通过if可输出无界解的情形。

    def FindMain(self):                 #按照θ规则寻找主元素，确定换入、换出变量
        j=self.C.index(max(self.C))     #确定换入变量j，即（获取检验数中最大值序号）
        special_count=0
        Theta=[]                        #θ
        for i in range(self.b_count):
            if self.bound[i][j]>0:      #除数必须大于零
                theta=self.bound[i][self.X_count]/self.bound[i][j] #θi=bi/aik
            else:
                theta=float('inf')      #给一个正无穷的数，便于排除掉
                if max(self.C)>0:
                    special_count+=1
                    if special_count==self.b_count:
                        self.special=False
            Theta.append(theta)
        i=Theta.index(min(Theta))       #确定换出变量i（获取检验数中最小值序号）
        main=self.bound[i][j]        
        return [i,j,main]

然后进行一次基变换

    #pivot(),基变换（旋转）
    def pivot(self):
        [i,j,main]=self.FindMain()  #单纯形法：寻找主元素
        self.B[i]=j                 #基变量中的换出变量替换为换入变量
        for x in range(self.X_count+1):	#变换基变量所在行
            self.bound[i][x]=self.bound[i][x]/main
        for k in range(self.b_count):	#变换其他行
            if k!=i:
                times=self.bound[k][j]  #倍数
                for t in range(self.X_count+1):
                    temp=self.bound[i][t]*times
                    self.bound[k][t]=self.bound[k][t]-temp        
    def Iteration(self):
            else: #否则，进行基变换（旋转）
                self.pivot()
                lim-=1

4.迭代直至结束

在Iteration()中通过while语句来迭代，解决的问题一般较为简单，如果迭代次数超过100可判定出现无限循环，此情况属于退化解无法解决的极少特例。
输出结果

    def Iteration(self):
        #如有最优解输出最优解和目标函数极值
        X=[0]*self.X_count
        count=0
        for i in self.B:
                X[i]=self.bound[count][self.X_count]
                count+=1
        Z=0
        for i in range(self.X_count):
            Z+=self.z[i]*X[i]
        if self.special==False:
            print("无界解")
        elif self.flag==1:
            print("有唯一最优解",X,Z)  
        elif self.flag==2: 
            print("存在无穷多最优解",X,"为最优解之一" , Z)
        elif self.flag==0:
            print("无解")

实例

1. 无界解
   
2. 唯一最优解
   
   
   
3. 无穷多最优解\两阶段法
   第一阶段
   
   min转化为max
   
   第二阶段
   

min转化为max，去掉人工变量。

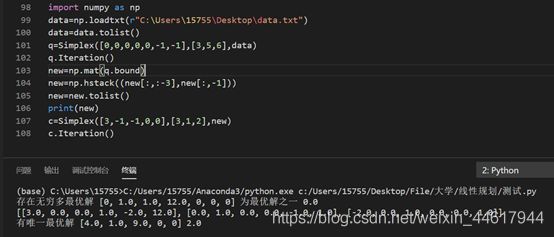
这里基变量一定要按照顺序输入！

对偶单纯形算法

思路同单纯形算法

整体代码

import numpy as np
class DualSimplex(object):
    #构造函数（初始化函数）
    def __init__(self,z,B,bound):  
        self.X_count=len(z)          #变量个数
        self.b_count=len(bound)      #约束条件个数
        self.z=z                     #目标函数
        self.C=[]                    #检验数
        self.B=B                     #基变量,由于运算规则必须按顺序给出基变量
        self.bound=bound             #约束条件,包括右端常数
        self.flag=0                  #解的类型，0为（暂时）无解，1为唯一最优解
        self.special=False           #约束条件所有系数大于等于0则无可行解
    #Iteration(),迭代函数
    def Iteration(self):    	
        lim=100		#防止无限迭代
        while(lim>0):
            self.C=[] #检验数清空
            for j in range(self.X_count):     
                zj=0
                for i in range(self.b_count): #遍历第j列全行系数，计算第j个变量检验数
                    zj+=self.bound[i][j]*self.z[self.B[i]]#限制B基变量序号顺序之处
                self.C.append(self.z[j]-zj) #检验数,'cj-zj'
            self.Check() #判断迭代是否结束
            if self.flag>0: #有解，结束迭代
                break
            else: #否则，进行基变换（旋转）
                self.pivot()
                lim-=1

        #如有最优解输出最优解和目标函数极值
        X=[0]*self.X_count
        count=0
        for i in self.B:
                X[i]=self.bound[count][self.X_count]
                count+=1
        Z=0
        for i in range(self.X_count):
            Z+=self.z[i]*X[i]
        if self.special:
            print("无可行解")
        elif self.flag==1:
            print("有唯一最优解",X,format(Z,'.2f'))  
        elif self.flag==0:
            print("无解")

    #Check()，检验是否为最优解
    def Check(self):   	
        self.flag=1
        for i in range(self.b_count):
            if self.bound[i][self.X_count]<0:		#若有约束条件右端常数为负，继续迭代
                self.flag=0
                break 

    #pivot(),基变换（旋转）
    def pivot(self):
        [i,j,main]=self.FindMain()  #单纯形法：寻找主元素
        self.B[i]=j                 #基变量中的换出变量替换为换入变量
        for x in range(self.X_count+1):	#变换基变量所在行
            self.bound[i][x]=self.bound[i][x]/main
        for k in range(self.b_count):	#变换其他行
            if k!=i:
                times=self.bound[k][j]  #倍数
                for t in range(self.X_count+1):
                    temp=self.bound[i][t]*times
                    self.bound[k][t]=self.bound[k][t]-temp

    def FindMain(self):                 #按照θ规则寻找主元素，确定换入、换出变量
        matbound=np.mat(self.bound)
        if np.min(matbound[:,:-1])>=0:
            self.special=True
        bi=[]
        for i in range(self.b_count):
            bi.append(self.bound[i][self.X_count])
        iout=bi.index(min(bi))          #确定换出变量  
        Theta=[]                        #θ
        for j in range(self.X_count):
            if self.bound[iout][j]>=0 or self.C[j]==0:      #被除数不为0，除数必须小于0
                theta=float('inf')      #给一个正无穷的数，便于排除掉
            else:
                theta=self.C[j]/self.bound[iout][j]
            Theta.append(theta)
        jin=Theta.index(min(Theta))      #确定换入变量
        main=self.bound[iout][jin]        
        return [iout,jin,main]
m=DualSimplex([-2,-3,-4,0,0],[3,4],[[-1,-2,-1,1,0,-3],[-2,1,-3,0,1,-4]])
n=m.Iteration()