POJ1436 线段树入门 区间标记
POJ1436 线段树入门
传送门
大概题意:
有n条垂直于x轴的线段,给定每条线段的 ‘y’ 范围和 'x’位置
当两条线段之间可以用一条不覆盖到其他线条且平行于X轴的线段连接时,定义两条线段相互见。求有多少 “两两可见的三条线段” 的数量。
思维:
首先把题目给的数据可视化一下(图有点丑)
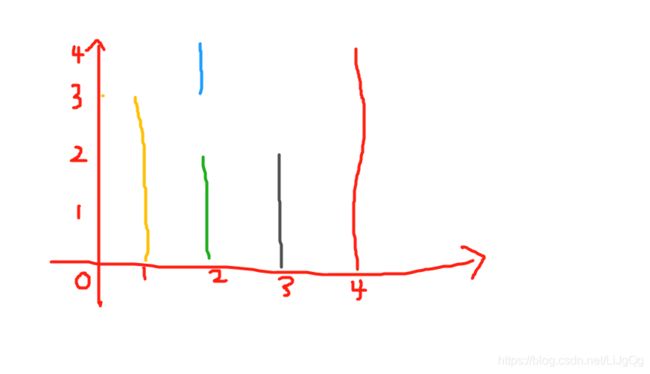
然后用肉眼观察(废话)
从左到右地看,发现只有 黄色 、蓝色 和 红色这一对能组成符合要求的三元组。
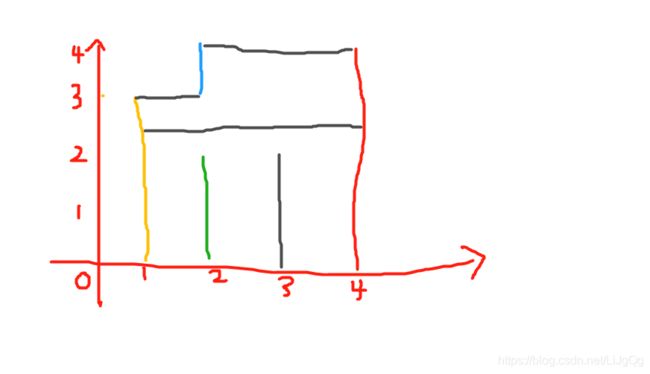
这样子看好像看不出什么,所以把图倒过来看看吧,顺便想象一下他们会落下来。
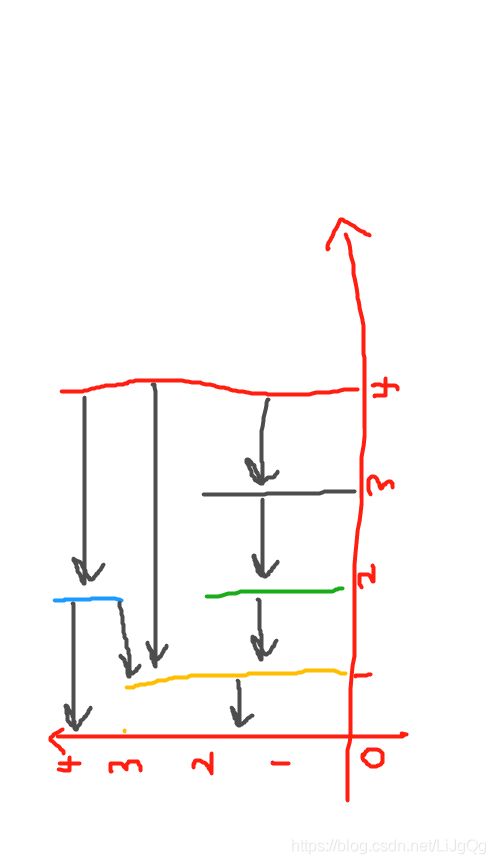
那么这里让比较靠近y轴的先落下来,我们会发现一些线段会压在其他线段上面,这时我们就把上面的线段用一个箭头指向下面的线段。
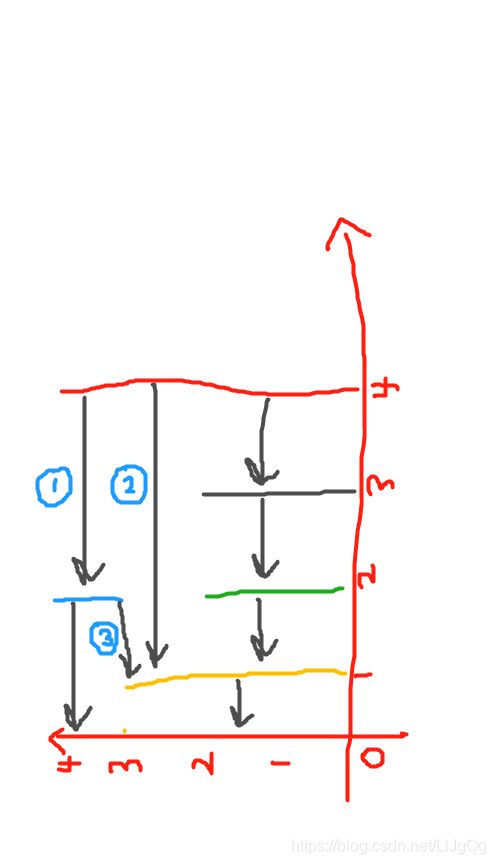
我们发现当箭头①指向的线段上连着箭头③,而箭头①出发的线段也有箭头②指向了同样的线段,这时这三个线段就满足了“两两相互可见”
所以我们可以让线段一段一段地落下来,然后落下来的时候,统计一下它压到了哪些线条,这样子就可以在用循环找出有多少对符合条件的三元组了。
算法:
对所有线段根据x轴位置从小到大进行排序
对y轴范围构建线段树
对所有线段依x轴位置升序进行以下操作:
- 查询当前线段y范围内压到了哪些线段,并记录下来
- 更新当前线段y范围内的线段为当前线段
对所有记录压到谁的数据进行统计,得出答案(不愿详细写,还是康代码吧hhh)
实现一:
#include
//对所有线段标记执行循环,从第二条开始循环,毕竟第一条只能压空气
for(int i = 2;i<total+1;++i){
//记录一下当前线段压到了哪些线段
int len = mark[i].size();
for(int j = 0;j<len;++j){
is[mark[i][j]] = i;
}
//对每一个被当前线段压到的线段执行循环
for(int j = 0;j<len;++j){
int to = mark[i][j];
int len = mark[to].size();
for(int k = 0;k<len;++k){
//如果这个线段有被当前线段压到的线段压到且当前线段也压到了这个线段
//就说明出现了符合题意三元组
//另外后边这个is语句好像没必要加上去hhh
if(is[mark[to][k]]&&is[mark[to][k]]!=to){
//记录一下算过这条线段了,防止重复计数,其实好像没必要的说,但是加上去好像更保险一些,说不定一不小心记录了两条相同的线段呢?
is[mark[to][k]] = to;
++ans;
}
}
}
//神奇的操作,我要取消记录当前线段压到了哪些线段
for(int j = 0;j<len;++j){
is[mark[i][j]] = false;
}
}
//输出答案
printf("%d\n",ans);
}
return 0;
}
实现二(自以为优化了,但其实好像没什么卵用,只说说优化的部分):
/*
==题意:有n条垂直于x轴的线段,给出他们y范围。
当两条线段之间有一条垂直于他们并且可以不经过其他线段,
则可定义两条线段互相可见,
求出有多少三条线段两两互相可见==
*/
#include
//另外去除了is的判断
for(int i = 2;i<total+1;++i){
int len = mark[i].size();
for(int j = 0;j<len;++j){
is[mark[i][j]] = i;
}
for(int j = 0;j<len;++j){
int to = mark[i][j];
int len = mark[to].size();
for(int k = 0;k<len;++k){
if(is[mark[to][k]]){
++ans;
}
}
}
for(int j = 0;j<len;++j){
is[mark[i][j]] = false;
}
}
printf("%d\n",ans);
}
return 0;
}