数据挖掘：模型选择——XGBoost与LightBGM

之前介绍了GBDT算法的一些知识，该算法的拟合能力很强，但由于是前向算法，所以运行起来会很慢，要等前面的结果出来后，才能拟合残差。陈天奇团队研究的XGBoost算法，可以解决这个问题，并且对GBDT有了很大的改进。

本文主要学习自B站up主：春暖花开Abela的视频，讲解的很透彻。（后面的知识有些听不懂了，直接截图的，大家可以去B站上的视频听这个老师讲课）

在有监督的学习任务里，一般有模型，参数，目标函数和学习方法。

• 模型：给定输入X后预测输出y的方法，比如回归，分类等。
• 参数：模型中的参数，比如线性回归y=ax+b中的权重a和偏置b
• 目标函数：即损失函数，包含正则项
• 学习方法：给定目标函数后求解模型的和参数的方法，比如梯度下降法，牛顿法等。

XGBoost相比GBDT的改进

第一，GBDT将目标函数泰勒展开到一阶，而xgboost将目标函数泰勒展开到了二阶。保留了更多有关目标函数的信息，对提升效果有帮助。

第二，GBDT是给新的基模型寻找新的拟合标签（前面加法模型的负梯度），而xgboost是给新的基模型寻找新的目标函数（目标函数关于新的基模型的二阶泰勒展开）。

第三，xgboost加入了和叶子权重的L2正则化项，因而有利于模型获得更低的方差。

第四，xgboost增加了自动处理缺失值特征的策略。通过把带缺失值样本分别划分到左子树或者右子树，比较两种方案下目标函数的优劣，从而自动对有缺失值的样本进行划分，无需对缺失特征进行填充预处理。

此外，xgboost还支持候选分位点切割，特征并行等，可以提升性能。

回顾

xgboost是gbdt的进阶版，而gbdt是由一堆cart树通过boosting集成算法得到的。
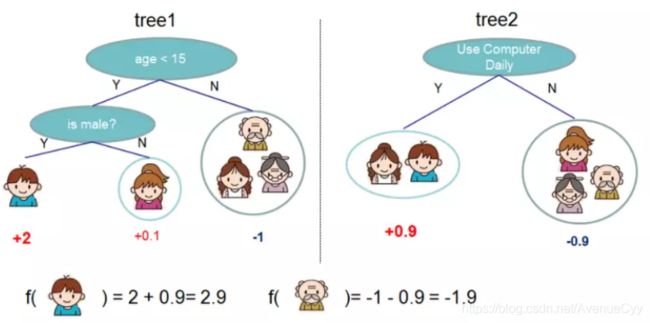
这里先看一下cart树的计算案例。回归树输出的是一个分数，表示这个人喜欢玩电脑游戏的程度，利用这个分数我们可以进行回归，或映射成概率进行分类。

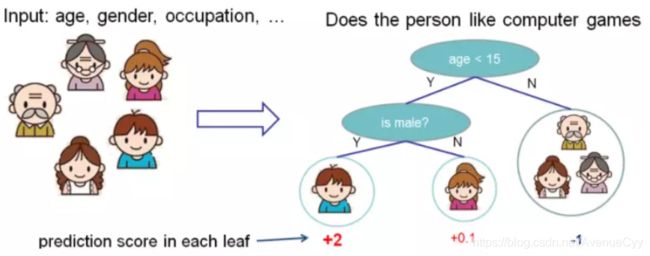
gbdt的计算案例。用两棵树进行预测，结果是两个树的和。

问题一：为什么xgboost用的是cart树，而不是别的呢？或者为什么是cart和boosting算法结合，而不是C4.5或者ID3？
在之前的树模型中有介绍，由于cart树是二叉树，计算结果会更快些。另外，对于分类问题，由于CART树的叶子节点对应的值是一个实际的分数，而非一个确定的类别，这将有利于实现高效的优化算法。

xgboost介绍

xgboost数学模型

xgboost利用前向分布算法，学习到包含K棵树的加法模型。这里的K就是树的棵数，F表示所有可能的CART树，f表示一棵具体的CART树。这个模型由K棵CART树组成。
这里面最重要的就是得到所有决策树，知道树的结构和叶子结点。

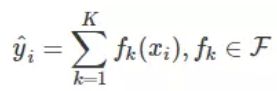
xgboost目标函数

这个目标函数包含两部分，第一部分就是损失函数（预测值和真实值之间的差距），第二部分就是正则项（衡量决策树的复杂程度，复杂程度越高，正则化向就越大，对损失函数的惩罚也大一些。），这里的正则化项由K棵树的正则化项相加而来。
我们的目标是为了优化这个目标函数，但因为f是决策树（包含树的结构和叶子结点的个数），不是数值型的向量，因此不能用梯度下降的算法进行优化。

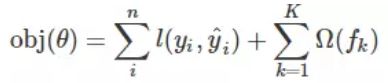
目标函数中损失函数的处理

xgboost是前向分布算法（通过一次次迭代，来获得当前的集成模型），通过贪心算法寻找局部最优解。第t次的结果，是第t-1次预测的结果，加上第t个弱分类器的结果。
要使损失函数最小，因为前t-1次的结果已经确定了，那么久需要找到第t棵树，使损失函数降低最多，以达到优化值。

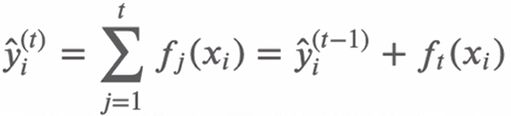
每次迭代都要寻找使损失函数降低最大的f(cart树)，所以，目标函数可以写成如下形式。
经过前t-1轮的迭代，决策树的结构个叶节点都已经确定了，所以前t-1次的正则化项就是常数了。因为要计算参数，使目标函数值最小，与常数无关，因此可以去掉。

接下来，采用泰勒展开对目标参数进行近似。
这里y(t-1)相当于x ^(t)，是我们已知的值。
f(x)相当于Δx。

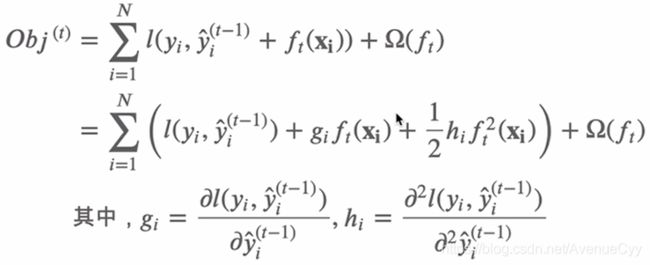
为什么用泰勒公式进行展开？
泰勒公式：是一个用函数在某点的信息描述其附近取值的公式。比如，我们知道x点的y1值，想计算出x+Δx处的y2值，此时就可以利用泰勒公式进行求解。
对于一般的函数，泰勒公式的系数的选择依赖于函数在一点的各阶导数值。函数f(x)在x0处的基本形式如下：

这里x^(t+1) = x ^(t)+Δx，类比于上一步得到的损失函数，对第t棵树进行一个近似。一般展开到2阶，就可以对所求值进行一个很好的近似效果。
所以，我们要对损失函数进行泰勒展开，展开到2阶即可。

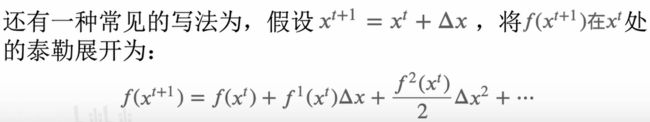
对目标函数来说，由于l(y,y(t-1))中没有参数，对t轮迭代来说是个常量，所以，可以移除。

目标函数中正则项的处理

树的复杂度可以用树的深度，内部节点个数，叶节点个数等来衡量。
目标函数中用正则项来衡量树的复杂度：树的叶子结点个数T和每棵树的叶子结点输出分数W的平方和（相当于L2正则化）。
公式如下。其中γ和λ是人为设置的数。

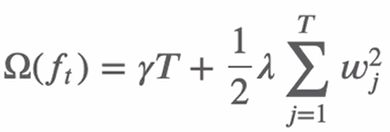
举个例子。比如要衡量这棵树的复杂程度。

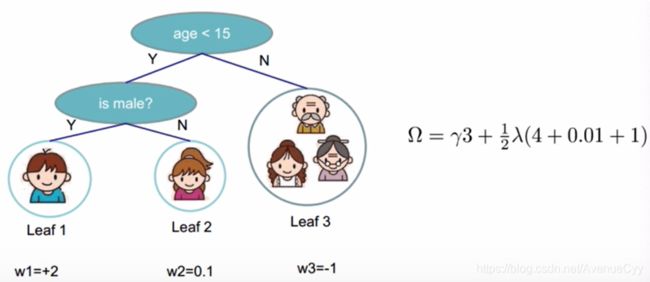
最终的目标函数

综上所述，xgboost的目标函数可以改写为如下形式。第一部分是对样本的累加（每个样本的计算值）。第二部分是正则项，是对叶节点的累加。

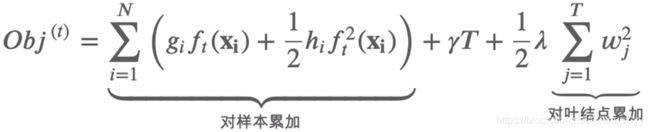
因为这两种累加形式不同，需要统一形式。这里转为都是对叶节点的累加。
定义一个函数q(x)，将输入x映射到某个叶子结点上。（对输入的每一个样本，求出该样本对应决策树的节点）
决策树f(x)就可以表示成wq(x)。
q(x)表示，对于样本x，输出其对应的叶子节点。q表示树的结构。
前面的w，计算该叶子节点的分数。w表示叶子结点的输出。

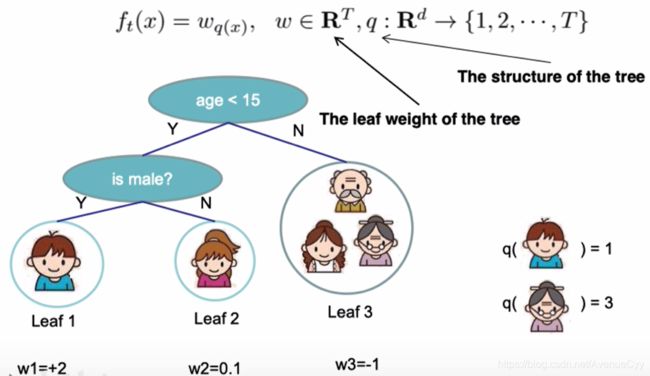
把样本的求和改为对叶子结点的求和。
I(j)：叶子结点上包含哪些样本。
对于每一个叶节点来说，遍历一下属于该叶节点的样本，来求giwi。
这里wj是我们要求解的，即每一个节点的输出是多少，是我们得到最终的结果。这里对w进行求导。

优化目标函数

接下来对目标函数进行优化，即计算第t轮时使得目标函数最小的叶节点的输出分数w，直接对w求导，使其导数为0.得到如下式子。

将其带入损失函数中。G^2/(H+λ)越大，目标函数越小。

目标函数计算案例

这是我们得到的第T棵树。这里的H4是H2.

学习方法

要确定模型，需要先确定决策树的结构。
决策树结构的生成，采用贪心算法，每次尝试分裂一个叶节点，计算分裂后的增益，选择增益最大的。在ID3中采用的是信息增益，C4.5中是信息增益比，CART中是Gini指数。

xgboost中计算增益的方法

损失函数如下。其中红色部分衡量了叶子结点对总体损失的贡献，红色部分越大，目标函数就越小。

在xgboost中增益计算方法如下。Gain的值越大，说明分裂后能使目标函数减小的越多。

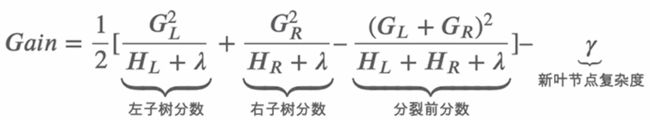
树结构的确定-精确贪心算法

枚举所有的特征和特征值，计算树的分裂方式。
I：当前节点的数据集。d：特征维度
增益Gain设为0。G：一阶导的和。H：二阶导的和。
遍历m棵树，
把左子树和右子树的一二阶梯度都设为0
对输入的特征排序，排序之后进行分裂，并对所有的分裂方式进行遍历：
计算左右子树的一二阶导
计算增益，选择增益最大的进行分裂

精确贪心算法弊端

首先进行排序，遍历每个特征，每一层都要做这种操作。计算的复杂度会很大。为了解决以上的问题，采用下面的近似算法。

树结构的确定-近似算法

近似算法有一个分桶的过程
遍历k棵树：
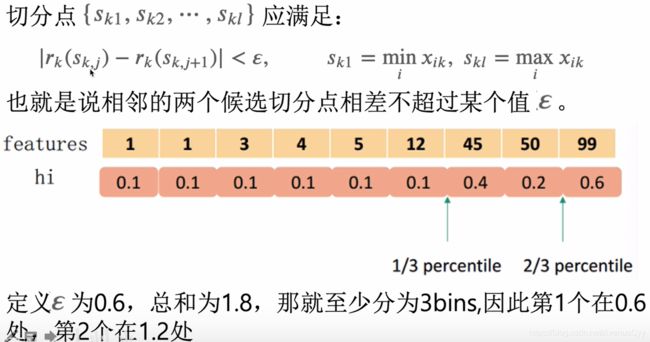
确定每个特征的候选切分点
计算每个划分点包含的一二阶梯度
接下来是对每个桶的数据进行一二阶导的求解。（感觉相当于数据分箱的操作1）
这样计算量会小一些，从N变量了L.

根据分位数给出对应的候选切分点。（但xgboost并没有这么做，这里只是提供这样的一种思路）
举个例子：

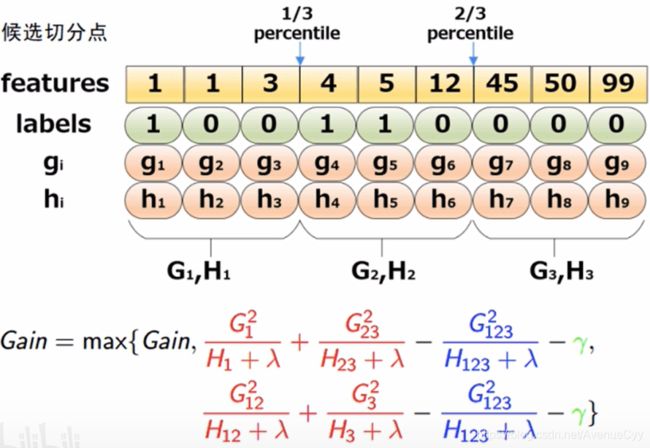
切分点的选取：全局策略(Global)和局部策略(Local)
Global：构建完一棵树后，不需要在某个叶节点划分的时候，再进行计算。
Local：每次分裂的时候，都需要重新划定切分点

以二阶梯度h为权重的分位数算法，来选取切分点。


为什么使用二阶梯度分桶？
将目标函数的泰勒展开如下所示。目标函数是 真实值为-gi/h，权重为hi 的平方损失，因此，使用二阶梯度加权。

树结构的确定-稀疏值处理

树结构的确定-步长

xgboost中的步长，也叫做收缩率。有助于防止过拟合，步长通常取0.1。

树结构的确定-列采样

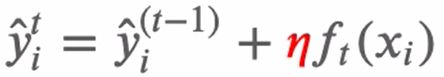
列采样，即对特征的采样。

系统设计

以上数学推导已经完毕，剩下的是计算机的相关知识。

系统设计-分块并行

在建树的过程中，最耗时的是寻找最优切分点，而这个过程最耗时的是将数据排序。为了减少排序时间，提出Block结构存储数据。

具体做法如下，这里不对缺失值进行排序。

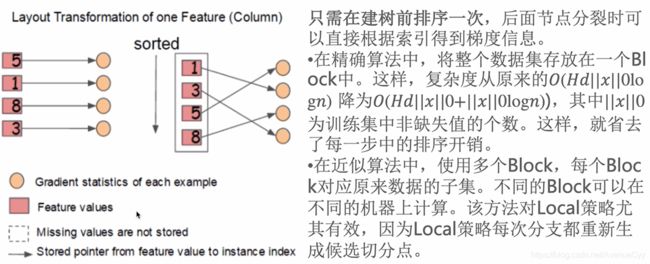
Block的缺点如下。其中梯度的顺序不是按照特征的大小顺序。

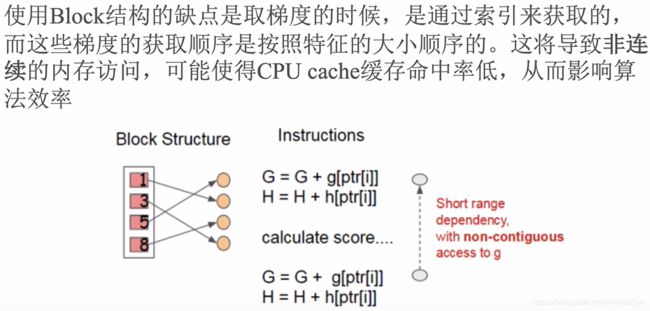
系统设计-缓存优化

精确算法的缓存优化：

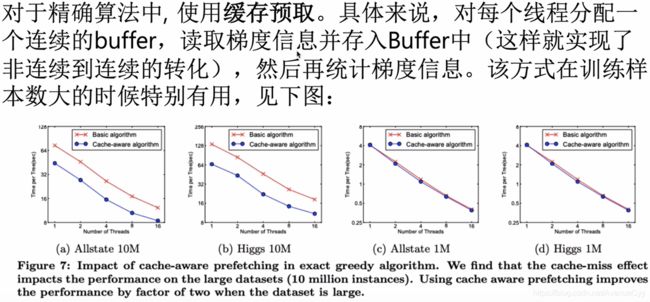
近似算法的缓存优化：

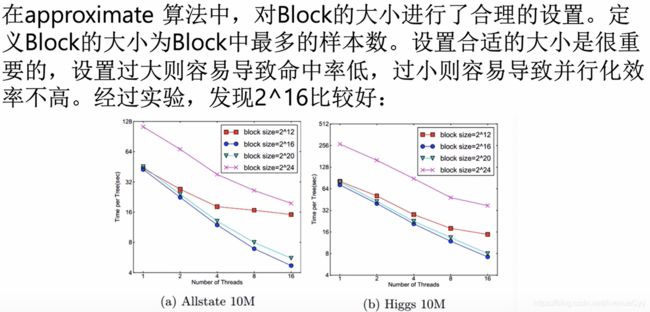
out of core Computation：

LightBGM介绍

LightBGM简介

由微软研究院开发，速度比XGBoost要快，精度也相当。它的设计理念为：

通过直方图找到最佳的分割点。
遍历T的所有叶节点：
遍历数据中的所有特征：
构建直方图
梯度信息
遍历所有的直方图里的每一个bins：
计算损失函数。

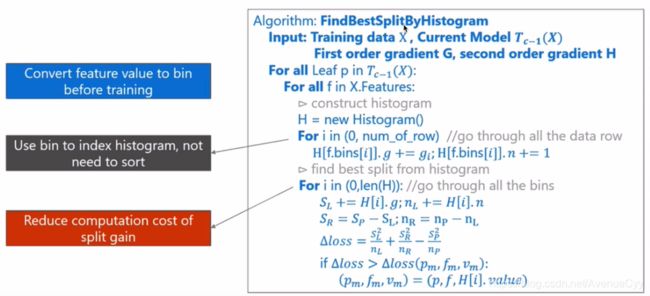
LightGBM与XGBoost对比：

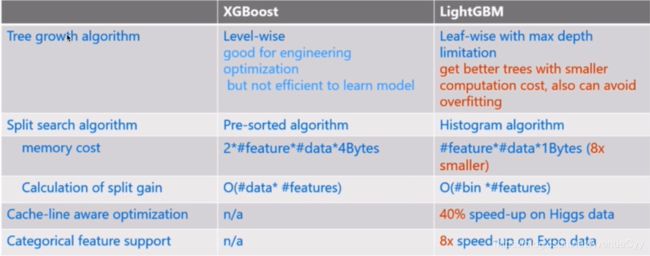
直方图算法

xgboost中精确贪心算法。

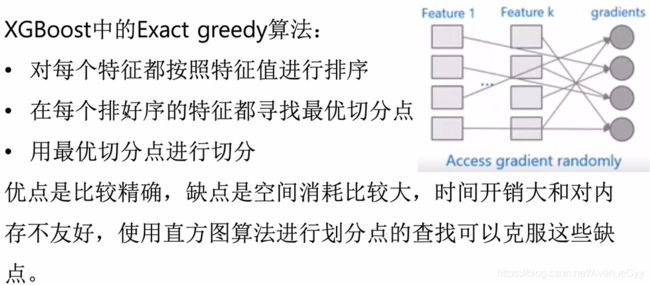
lightgbm中的直方图算法。

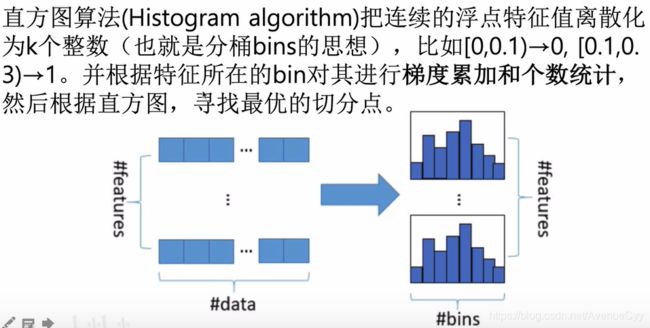
I：训练数据，d：最大深度，m：特征维度

直方图算法-如何分桶

数值型特征和分类特征采用不同的方法。
数值型特征：

分类型特征：

直方图算法-直方图构建

但是每个每个节点去计算直方图比较慢，这里采用直方图作差法。

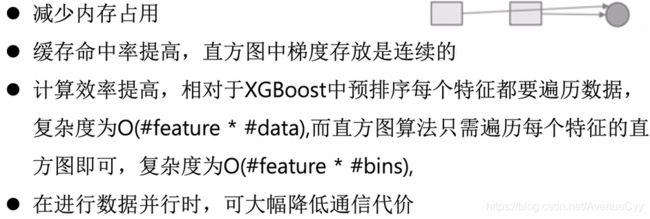
直方图算法优点

直方图算法改进

lightgbm中提出了降低特征维度的方法：GOSS算法和EFB算法。

直方图算法改进-GOSS算法

根据梯度来对样本进行采样。主要倚重大梯度的样本，对小梯度的样本考虑小一些。

a：大梯度样本在所有样本中的比例
b：小梯度样本在所有样本中的比例

直方图算法改进-EFB算法

EFB算法主要针对高维特征中，为0的稀疏特征。对特征进行合并。先对互斥的特征进行合并（比如独热编码后的特征），对合并后的特征进行划分。

判断哪些特征可以合并：

如何进行特征合并：

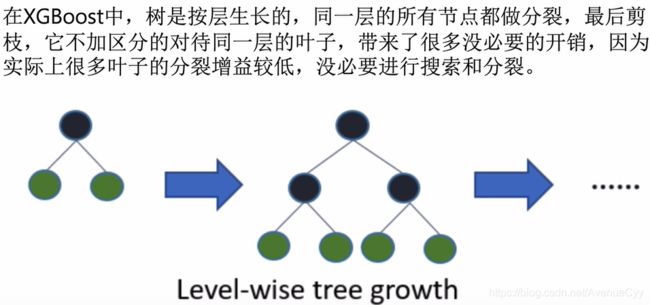
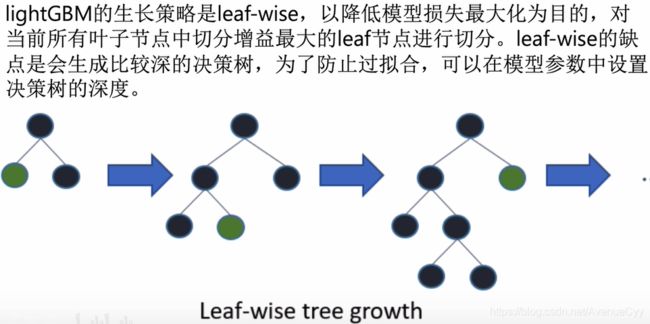
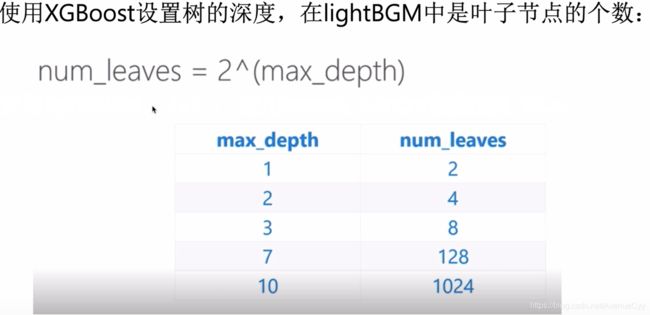
LightBGM树的生长策略

树的构建过程中，节点是如何分裂的。

LightBGM系统设计

lightbgm支持高效并行的特点目前支持：

LightBGM系统设计-特征并行

特征并行分为两类：传统算法和lightgbm算法。
传统算法：

lightgbm算法：

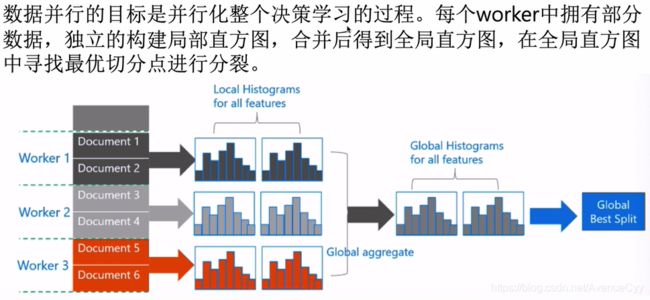
LightBGM系统设计-数据并行

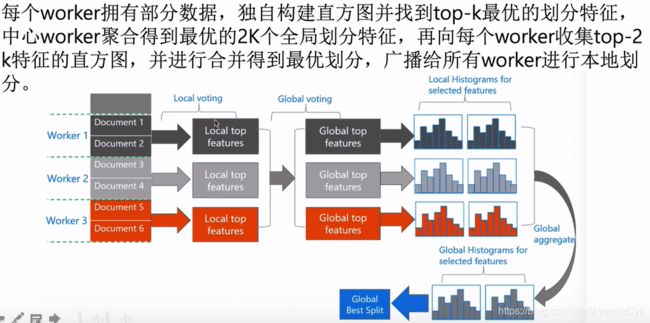
LightBGM系统设计-投票并行

LightGBM实践

参考文献

https://www.bilibili.com/video/BV1Ca4y1t7DS?p=11