數據集的相似性計算,其應用十分廣汎,在現有的各類人工智能的底層算法中,大多數都是基於概率(可能性)的近似計算,然後取最大可能性的近似值。參考 理解计算:从根号2到AlphaGo ——第1季 从根号谈起 ( https://ufqi.com/news/ulongpage.191.html )。 另外使用神經網絡可以模擬任意曲綫函數,A visual proof that neural nets can compute any function ( http://neuralnetworksanddeeplearning.com/chap4.html ) 。
甚至,在早期的搜索引擎的計算中,如果計算兩個段落或者兩篇文章的相似性,也有使用基於圖的算法,將每篇文章視爲一個 graph,然後使用下面的圖的相似性的算法來計算兩者之間的相似性。
從一堆圖片中找到貓的照片是類似算法,車牌識別是這種算法,人臉識別、語音識別等都是類似的應用,神經網絡、深度學習等,莫不如是。人工智能AI之外,我們看到各種基於興趣的商品推薦,在綫廣告的智能匹配等等,都有這些算法的身影。
我們曾經開展過在綫廣告點擊率預測模型,其中運用到KNN算法,其核心就用到了 Euclidean Distance的計算 ( https://www.researchgate.net/publication/330742123_A_practical_study_on_imbalanced_data_re-sampling_for_conversion_rate_of_online_advertising ) 。
Neo4j 關於圖(Graph)的相似性計算(Similarity algorithm)提供了若干算法。
https://neo4j.com/docs/graph-data-science/current/alpha-algorithms/
- 5.4.1. Node Similarity
- 5.4.2. Jaccard Similarity
- 5.4.3. Cosine Similarity
- 5.4.4. Pearson Similarity
- 5.4.5. Euclidean Distance
- 5.4.6. Overlap Similarity
- 5.4.7. Approximate Nearest
這些算法都有詳細的解釋説明,樣例代碼等,這裏還有對幾種不同算法的對比分析(參考:余弦距离、欧氏距离和杰卡德相似性度量的对比分析 , https://www.jianshu.com/p/c4bbad87f873 )。 其中應用較多的是 餘弦距離和歐氏距離。
Cosine Similarity/餘弦距離計算公式
Euclidean Distance/歐氏距離計算公式
在 Neo4j 的文檔中,對餘弦距離和歐氏距離的應用場景都有差不多的描述:
我们可以使用欧几里德距离算法来计算两个事物之间的相似性。然后我们可以使用计算出的相似度作为推荐查询的一部分。例如,根据用户的偏好来获得电影推荐,这些用户所給出的评分与您看过的其他电影的评分相似。
We can use the Cosine Similarity algorithm to work out the similarity between two things. We might then use the computed similarity as part of a recommendation query. For example, to get movie recommendations based on the preferences of users who have given similar ratings to other movies that you’ve seen.
Neo4j是一個開源的NoSQL的原生圖數據庫。Neo4j is an open-source, NoSQL, native graph database that provides an ACID-compliant transactional backend for your applications.
圖數據庫存儲的數據單位是節點(Node)和關係(Relations)。
通常,圖用一組數據表示,如 g1(a0, a1, a2, a3, ….), g2(b0, b1, b2, b3, ….),極值情況下,如 g1(a0), g2(b0) 如何比較和計算相似性?這是本文試圖探討的要點。我們還結合研發中的  有福工坊UfqiWork ( https://ufqi.com/work ) 的實際應用案例對所提議的算法進行了驗證,取得了預期的效果。
有福工坊UfqiWork ( https://ufqi.com/work ) 的實際應用案例對所提議的算法進行了驗證,取得了預期的效果。
將極值比如 g1(10) 和 g(100) 進行計算時,幾乎每個算法都會返回極其不相似的結果值: -1 .
如果我們想進一步地探討, g1(10) 和 g2(100) 的不相似值, 與 g2(100) 和 g3(1000) 的不相似值,有多少程度上的不同呢? 顯然上面的算法在都返回不相似的極值 -1 時,兩者的不相似是一樣的,而真實情況真的是一樣嗎?如果不一樣,怎麽來描述這種不相似的差異?
簡單而直接的做法是考察兩個數值之間的減法差值或除法商值,差值或商值的大小決定了兩個數據的差異性,正比例關係。
比如,10~100的差值是90,商值是10, 100~1000的差值是900,商值是10.
如果我們要定義或者套用一下相似性,10~100的相似性用數值表達是多少? 100~1000的相似性用數值表達是多少?如果比較差值的話,後者的差別大於前者,如果比較商值的話,前者與後者相等。從語義上來解讀,顯然使用商值較符合預期,業績兩者的差異是10倍。
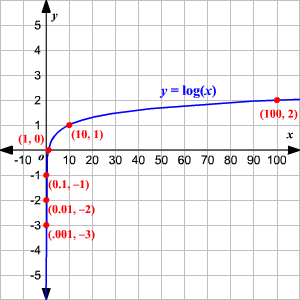
使用絕對商值10來描述相似性顯然不太合適,爲了便於表述為相似性,我們還需要對其進行歸一化處理。為方便描述兩個數值的商值,我們對商值取log10對數,這樣大幅降低絕對值的範圍並提供更大的曲綫表述空間,其絕對值的細微變化能夠映射到相應的對數值上。
嘗試進行歸一化(Normalization)處理時,需要設定區間閾值。如果兩個數相等,其商值為1,取對數log10(1)時, 得到值為 0,可以認爲儅兩個數的如上這麽計算過程之後值為0時,這兩個數的相似性是 100%。
那麽,多大是不相似呢?如果做歸一化或者百分比,我們需要確定、劃定一個“不相似值”的標準,無論是取商值,還是再對商值取對數,需要一個明確而具體的數值來表示或界定完全不相似。這個數值可能最終需要靠經驗獲得,也與要考察的數據可能的取值範圍有關,比如考察人的身高時,相差一倍就有種十萬八千裏的感覺;而考察星系,十萬八千里也可能只是一倍的表述。因此,這個用以界定“不相似”的閾值 k 應該是根據經驗和應用場景而定。
於是,我們就可以寫出我們用於求值某兩個任意數的相似性值,設若k為完全不相似,則某兩個數的相似性表述區間為 [0, k] , 針對這個取值範圍,再進行歸一化處理則相對容易。最終,我們擬寫了下面這個求取兩個任意數值的相似性的函數表達式:
F(n1, n2, k) = normalize{ min[k, log10[ max(n1, n2)/min(n1, n2)] ] };
其中n1, n2為待求取相似性的兩個數值, k為經驗常數極值(表示完全不相似值)。
其計算過程可以描述爲:
1) 比較n1, n2的大小;
2) 求取n1, n2較大值除以較小值的商;
3) 對商值取log10對數;
4) 比較對數值與常熟k的大小,如果商值的對數值大於k,取k值;
5) 對前一步數值做歸一化處理,得到預期值在 [0, 1] 之間.
由此,我們獲知,儅兩個數的商值一樣時,其相似性是一樣的。因此10~100 和 100~1000的相似性是一樣的。對商值做進一步的處理是爲了表述和運算方便。類似的算法我們在  有福工坊UfqiWork ( https://ufqi.com/work ) 進行試用,取得了一定的預期效果。
有福工坊UfqiWork ( https://ufqi.com/work ) 進行試用,取得了一定的預期效果。
圖的極值問題只是相似性問題中的特例,同時這些所謂的極值也是相對的,儅g1(a1), g2(a2), g3(a3)…. 等多個極值組合為一個大的圖G(a1, a2, a3….)時,其與另外一個大G(b1, b2, b3…)相比較計算相似性時,又回歸到到文檔看到提到的數據集相似性問題計算了。
[
](https://ufqi.com/work)UfqiWork 有福工坊 服務交易所
有福工坊UfqiWork 是一个在线服务交易平台。
有福工坊提供在线分类服务信息,致力于在线撮合服务交易的买方和卖方,并为买方、卖方提供“行准”服务,居间担保服务交易。行准服务的提供方为居间交易的第三方。有福工坊的服务交易平台为整个服务交易流程的第四方。
线上签约,线下交割。有福工坊整合服务交易的 信息流和 资金流,在线承载买卖双方的需求供给信息匹配、交易撮合,在线承担交易双方的资金拨付、担保。服务交易的 标的物在线下实施、交割。
有福工坊服务交易平台服务于提供居间交易的“行准”,通过行准服务于服务交易的买卖双方。交易标的物与其他电子商务交易不同的是其非标准性,如房屋、工作/职业、家政/维保、汽车、医疗、教育、金融、出行、时尚等等。相应地行准为房产中介,猎头中介,商品导购、推荐、带货等。
所不同于现有分类市场的地方在于:站在买方立场代表买方利益的居间服务;买方有定价权,居间服务报价。相应地,卖方也可以使用定价权雇佣代表卖方立场和利益的居间服务。
有福工坊UfqiWork 圖標中 “有” 的紅色高亮部分,既像是“房屋”(住房),也像是“凳子”(工作),寓意 有福工坊UfqiWork 致力於為用戶提供住房、工作、家政等各類信息匹配及撮合交易服務。
https://ufqi.com/blog/graph-similarity-algorithm-polar-neo4j/