蚁群算法汇总含matlab代码_数学建模(十四)

蚁群算法模拟自然界蚂蚁群体的觅食行为，常用于旅行商问题（TSP），二维、三维路径规划问题。
将蚁群算法用于优化问题的思路：用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也越来越多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。
使用蚁群算法解决问题的基本步骤如下：

图1 蚁群算法解决TSP问题的基本步骤
1：初始化参数
在计算之初，需要对相关的参数进行初始化，如蚁群规模、信息素重要程度因子、启发函数重要程度因子，信息素挥发因子，信息素释放总量，最大迭代次数，迭代数初值。
2：构建解空间
将各个蚂蚁随机地置于不同出发点，对每个蚂蚁k，计算其下一个待访问的城市，直到所有蚂蚁访问完所有的城市。
3：更新信息素
计算各个蚂蚁经过的路径长度，记录当前迭代次数中的最优解（最短路径）。同时，对各个城市连接路径上的信息素浓度进行更新。
4：判断是否终止
若iter

蚁群算法的特点：
（1）采用正反馈机制，使得搜索过程不断收敛，最终逼近最优解。
（2）每个个体可以通过释放信息素来改变周围的环境，且每个个体能够感知周围环境的实时变化，个体间通过环境进行间接地通讯。
（3）搜索过程采用分布式计算方法，多个个体同时进行并行计算，大大提高了算法的计算能力和运行效率。
（4）启发式的概率搜索方法不容易陷入局部最优解，易于寻找到全局最优解。

我们以中国31个直辖市、省会、自治区（未包括我国香港、澳门及台湾）

求解结果如下：

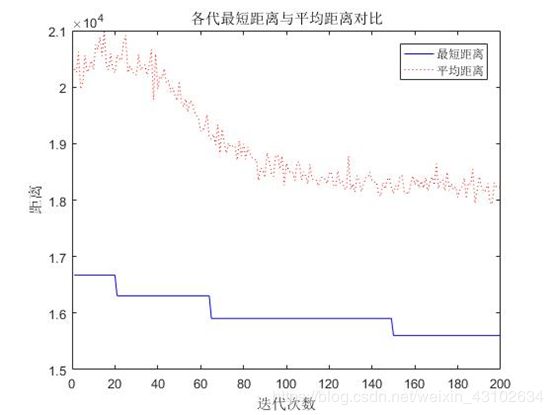
图2 TSP的最短距离与迭代次数的关系图

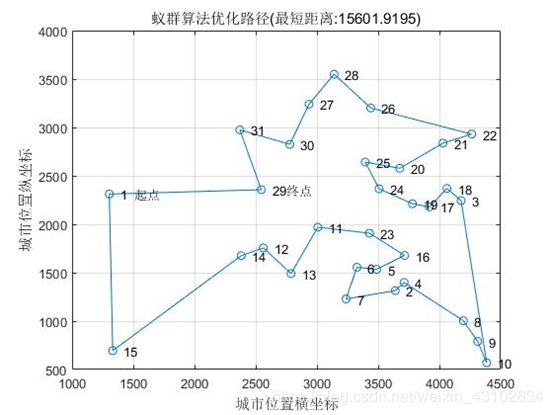
图3 蚁群算法优化路径

二维路径规划问题：
路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点、无碰撞地绕过所有障碍物的运动路径。
我们以一个具体问题为例：
采用蚁群算法在200200的二维空间中寻找一条从起点S到终点T的最优路径，该二维空间中存在4个障碍物，障碍物1的4个顶点的坐标分别为（40 140；60 160；100 140；60 120），障碍物2的4个顶点分别为（50 30；30 40；80 80；100 40），障碍物3的4个顶点分别为（120 160；140 100；180 170；165 180），障碍物4的3个顶点分别为（120 40；170 40；140 80），其中点S为起点，起点坐标为（20,180）；点T为终点，终点坐标为（160,90）。
求解结果：

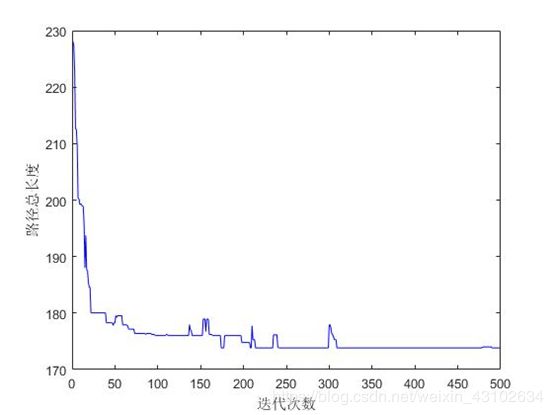
图4 适应度值变化

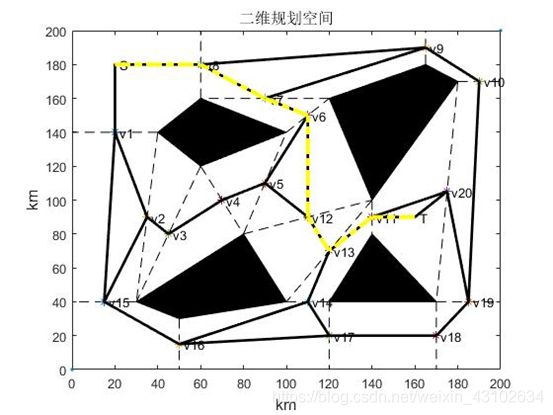
图5 路径规划结果
三维路径规划问题：
采用蚁群算法在跨度为21km21km的一片海域中搜索从起点到终点，并且避开所有障碍物的路径，为了方便问题的求解，取该区域内最深点的高度为0，其他点高度根据和最深点高度差依次取得。路径规划起点坐标为（1,10,800），终点坐标为（21,4,1000），规划环境和起点、终点如图：

图6 三维路径搜索空间
求解结果如图：

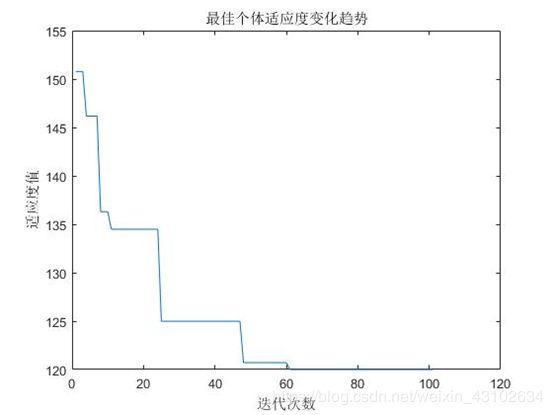
图7 适应度值变化

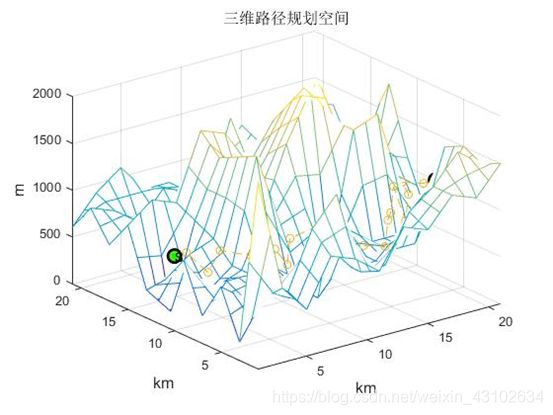
图8 路径规划结果
参考文献：
[1]DORIGO M,GAMBARDELLA L M. Ant Colonies for the Traveling Salesman Problem[J]. BioSystems,1997,43(2):73-81.
[2]DORIGO M,GAMBARDELLA L M Ant Colony System:a Cooperative Learning Approach to the Traveling Salesman Problem[J].IEEE Transaction on Evolutionary Computation,1997,1(1):53-66.
[3]DORIGO M,BIRATTARI M,STUTZLE T. Ant Colony Optimization[J].Computational Intelligence Magazine,2006,1(4):28-39.
[4]STUTZLE T D M.A Short Convergence Proof for a Class of Ant Colony Optimization Algorithms[J].IEEE Transactions on Evolutionary Computation,2002,6(4):358-365.
[5]萧蕴诗，李炳宇，吴启迪.求解TSP问题的模式学习并行蚁群算法[J].控制与决策，2004,19（8）：885-888.
[6]吴斌，史忠植.一种基于蚁群算法的 TSP问题分段求解方法[J].计算机学报，2001，24(12):1328-1333
[7]王颖，谢剑英.一种自适应蚁群算法及其仿真研究[J].系统仿真学报,2002.14(1):31 -33.
[8]叶志伟，郑肇葆.蚁群算法中参数 设置的研究——以 TSP问题为例[J].武汉大学学报:信息科学版.2004.29(7):597 - 601.
[9]胡小兵，黄席樾.对一类带聚类特征 TSP问题的蚁群算法求解[J].系统仿真学报，2004,16(12)：
2683 - 2686.
[10] 徐精明，曹先彬，王煦法.多态蚁群算法[J].中国科学技术大学学报，2005，35(1):59- 65.

[11]XI Y G.ZHANG C G. Rolling Path Planning of Mobile Robot in a Kind of Dynamic Uncertain Environment[J]. Acta Automatica Sinica,2002,28:161 - 175.
[12] COLONIA DORIGO M. MANIEZZO V. Distributed Optimization by Ant Colonies[EB/OL]. [2010 -
09]. ftp://iridia. ulb. ac. be/ pub/ mdorigo/ conference/IC.06 - ECAL92. pdf.
[13] DORIGO M, MANIEZZO V, COLONI A. The Ant System: Optimization by a Colony of Cooperating
Agents[ EB/OL]. [2010- 09]. http://ieeexplore.ieee.org/xpl/freeabs_ all. jsp? arnumber=484436.
[14] DORIGO M, GAMBARDELLA L M. Ant Colony System: a Cooperative Learning Approach to the Traveling Salesman Problem[J]. IEEE Transaction on Evolutionary Computation. 1997,1:53 - 66.

[15]张京娟.基于遗传算法的水下潜器自主导航规划技术研究[D].哈尔滨:哈尔滨工程大学,2003.
[16] WARREN C W. A Technique for Autonomous Underwater Vehicle Route Planning[J]. IEEE Journal of Oceanic Engineering, 1990,15(3):199 - 204.
[17] VASUDEVAN C. GANESAN L. Case based Path Planning for Autonomous Underwater Vehicles[J]. Autonomous Robots, 1996,3(2):79 - 89.
[18]田峰敏.基于先验地形数据处理的水下潜器地形辅助导航方法研究[D].哈尔滨:哈尔滨工程大学2007.
附录：matlab代码：
TSP问题求解代码：

%% 清空环境变量
clear all
clc

%% 导入数据
load citys_data.mat

%% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
m = 50;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.1;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 200;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max,1);     % 各代最佳路径的长度  
Length_ave = zeros(iter_max,1);      % 各代路径的平均长度  

%% 迭代寻找最佳路径
while iter <= iter_max
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,1);
      for i = 1:m
          temp = randperm(n);
          start(i) = temp(1);
      end
      Table(:,1) = start; 
      % 构建解空间
      citys_index = 1:n;
      % 逐个蚂蚁路径选择
      for i = 1:m
          % 逐个城市路径选择
         for j = 2:n
             tabu = Table(i,1:(j - 1));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,tabu);
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = 1:length(allow)
                 P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
             Pc = cumsum(P);     
            target_index = find(Pc >= rand); 
            target = allow(target_index(1));
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,1);
      for i = 1:m
          Route = Table(i,:);
          for j = 1:(n - 1)
              Length(i) = Length(i) + D(Route(j),Route(j + 1));
          end
          Length(i) = Length(i) + D(Route(n),Route(1));
      end
      % 计算最短路径距离及平均距离
      if iter == 1
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;  
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - 1),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
          else
              Route_best(iter,:) = Route_best((iter-1),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = 1:m
          % 逐个城市计算
          for j = 1:(n - 1)
              Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
      end
      Tau = (1-rho) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表
    iter = iter + 1;
    Table = zeros(m,n);
end

%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);

%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
     [citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
    text(citys(i,1),citys(i,2),['   ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),'       起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')

%%

二维路线规划代码：
%% 清空环境
clc;clear

%% 障碍物数据
position = load('barrier.txt');
plot([0,200],[0,200],'.');
hold on
B = load('barrier.txt');
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
title('二维规划空间','fontsize',12)
%% 描述起点和终点
S = [20,180];
T = [160,90];
plot([S(1),T(1)],[S(2),T(2)],'.');

% 图形标注
text(S(1)+2,S(2),'S');
text(T(1)+2,T(2),'T');
 
%% 描绘障碍物图形
fill(position(1:4,1),position(1:4,2),[0,0,0]);
fill(position(5:8,1),position(5:8,2),[0,0,0]);
fill(position(9:12,1),position(9:12,2),[0,0,0]);
fill(position(13:15,1),position(13:15,2),[0,0,0]);

% 下载链路端点数据
L = load('lines.txt');
 
%% 描绘线及中点
v = zeros(size(L));
for i=1:20
    plot([position(L(i,1),1),position(L(i,2),1)],[position(L(i,1),2)...
        ,position(L(i,2),2)],'color','black','LineStyle','--');
    v(i,:) = (position(L(i,1),:)+position(L(i,2),:))/2;
    plot(v(i,1),v(i,2),'*');
    text(v(i,1)+2,v(i,2),strcat('v',num2str(i)));
end
 
%% 描绘可行路径
sign = load('matrix.txt');
[n,m]=size(sign);
 
for i=1:n
    
    if i == 1
        for k=1:m-1
            if sign(i,k) == 1
                plot([S(1),v(k-1,1)],[S(2),v(k-1,2)],'color',...
                    'black','Linewidth',2,'LineStyle','-');
            end
        end
        continue;
    end
    
    for j=2:i
        if i == m
            if sign(i,j) == 1
                plot([T(1),v(j-1,1)],[T(2),v(j-1,2)],'color',...
                    'black','Linewidth',2,'LineStyle','-');
            end
        else
            if sign(i,j) == 1
                plot([v(i-1,1),v(j-1,1)],[v(i-1,2),v(j-1,2)],...
                    'color','black','Linewidth',2,'LineStyle','-');
            end
        end
    end
end
path = DijkstraPlan(position,sign);
j = path(22);
plot([T(1),v(j-1,1)],[T(2),v(j-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');
i = path(22);
j = path(i);
count = 0;
while true
    plot([v(i-1,1),v(j-1,1)],[v(i-1,2),v(j-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');
    count = count + 1;
    i = j;
    j = path(i);
    if i == 1 || j==1
        break;
    end
end
plot([S(1),v(i-1,1)],[S(2),v(i-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');


count = count+3;
pathtemp(count) = 22;
j = 22;
for i=2:count
    pathtemp(count-i+1) = path(j);
    j = path(j);
end
path = pathtemp;
path = [1     9     8     7    13    14    12    22];

%% 蚁群算法参数初始化
pathCount = length(path)-2;          %经过线段数量
pheCacuPara=2;                       %信息素计算参数
pheThres = 0.8;                      %信息素选择阈值
pheUpPara=[0.1 0.0003];              %信息素更新参数
qfz= zeros(pathCount,10);            %启发值

phePara = ones(pathCount,10)*pheUpPara(2);         %信息素
qfzPara1 = ones(10,1)*0.5;           %启发信息参数
qfzPara2 = 1.1;                      %启发信息参数
m=10;                                %种群数量
NC=500;                              %循环次数
pathk = zeros(pathCount,m);          %搜索结果记录
shortestpath = zeros(1,NC);          %进化过程记录
 
%% 初始最短路径
dijpathlen = 0;
vv = zeros(22,2);
vv(1,:) = S;
vv(22,:) = T;
vv(2:21,:) = v;
for i=1:pathCount-1
dijpathlen = dijpathlen + sqrt((vv(path(i),1)-vv(path(i+1),1))^2+(vv(path(i),2)-vv(path(i+1),2))^2);
end
LL = dijpathlen;
 
%% 经过的链接线
lines = zeros(pathCount,4);
for i = 1:pathCount
    lines(i,1:2) = B(L(path(i+1)-1,1),:);
    lines(i,3:4) = B(L(path(i+1)-1,2),:);
end
 
%% 循环搜索
for num = 1:NC
    
    %% 蚂蚁迭代寻优一次
    for i=1:pathCount
        for k=1:m
            q = rand();
            qfz(i,:) = (qfzPara2-abs((1:10)'/10-qfzPara1))/qfzPara2; %启发信息
            if q<=pheThres%选择信息素最大值
                arg = phePara(i,:).*(qfz(i,:).^pheCacuPara);
                j = find(arg == max(arg));
                pathk(i,k) = j(1);
            else  % 轮盘赌选择
                arg = phePara(i,:).*(qfz(i,:).^pheCacuPara);
                sumarg = sum(arg);
                qq = (q-pheThres)/(1-pheThres);
                qtemp = 0;
                j = 1;
                while qtemp < qq
                    qtemp = qtemp + (phePara(i,j)*(qfz(i,j)^pheCacuPara))/sumarg;
                    j=j+1;
                end
                j=j-1;
                pathk(i,k) = j(1);
            end
            % 信息素更新
            phePara(i,j) = (1-pheUpPara(1))*phePara(i,j)+pheUpPara(1)*pheUpPara(2);
        end
    end
    
    %% 计算路径长度
    len = zeros(1,k);
    for k=1:m
        Pstart = S;
        Pend = lines(1,1:2) + (lines(1,3:4)-lines(1,1:2))*pathk(1,k)/10;
        for l=1:pathCount
            len(1,k) = len(1,k)+sqrt(sum((Pend-Pstart).^2));
            Pstart = Pend;
            if l<pathCount
                Pend = lines(l+1,1:2) + (lines(l+1,3:4)-lines(l+1,1:2))*pathk(l+1,k)/10;
            end
        end
        Pend = T;
        len(1,k) = len(1,k)+sqrt(sum((Pend-Pstart).^2));
    end
    
    %% 更新信息素
    % 寻找最短路径
    minlen = min(len);
    minlen = minlen(1);
    minant = find(len == minlen);
    minant = minant(1);
    
    % 更新全局最短路径
    if minlen < LL
        LL = minlen;
    end
    
    % 更新信息素
    for i=1:pathCount
        phePara(i,pathk(i,minant)) = (1-pheUpPara(1))* phePara(i,pathk(i,minant))+pheUpPara(1)*(1/minlen);
    end
    shortestpath(num) = minlen;
end

figure;
plot(1:NC,shortestpath,'color','blue');
hold on
% plot(1:NC,dijpathlen,'color','red');
ylabel('路径总长度');
xlabel('迭代次数');

function path = DijkstraPlan(position,sign)
%% 基于Dijkstra算法的路径规划算法
%position    input     %节点位置
%sign        input     %节点间是否可达
 
%path        output    %规划路径
 
%% 计算路径距离
cost = ones(size(sign))*10000;
[n,m] = size(sign);
for i = 1:n
    for j = 1:m
        if sign(i,j) == 1
            cost(i,j) = sqrt(sum((position(i,:)-position(j,:)).^2));
        end
    end
end
 
%% 路径开始点
dist = cost(1,:);             %节点间路径长度           
s = zeros(size(dist));        %节点经过标志
s(1) = 1;dist(1) = 0;
path = zeros(size(dist));     %依次经过的节点
path(1,:) = 1;
 
%% 循环寻找路径点
for num = 2:n   
    
    % 选择路径长度最小点
    mindist = 10000;
    for i = 1:length(dist)
        if s(i) == 0
            if dist(i)< mindist
                mindist = dist(i);
                u = i;
            end
        end
    end
    
    % 更新点点间路径
    s(u) = 1;
    for w = 1:length(dist)
        if s(i) == 0
            if dist(u)+cost(u,w) < dist(w)
                dist(w) = dist(u)+cost(u,w);
                path(w) = u;
            end
        end
    end
end

三维路线规划代码：
%% 该函数用于演示基于蚁群算法的三维路径规划算法

%% 清空环境
clc
clear

%% 数据初始化

%下载数据
load  HeightData HeightData

%网格划分
LevelGrid=10;
PortGrid=21;

%起点终点网格点 
starty=10;starth=4;
endy=8;endh=5;
m=1;
%算法参数
PopNumber=10;         %种群个数
BestFitness=[];    %最佳个体

%初始信息素
pheromone=ones(21,21,21);

%% 初始搜索路径
[path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone, ...
    HeightData,starty,starth,endy,endh); 
fitness=CacuFit(path);                          %适应度计算
[bestfitness,bestindex]=min(fitness);           %最佳适应度
bestpath=path(bestindex,:);                     %最佳路径
BestFitness=[BestFitness;bestfitness];          %适应度值记录
 
%% 信息素更新
rou=0.2;
cfit=100/bestfitness;
for i=2:PortGrid-1
    pheromone(i,bestpath(i*2-1),bestpath(i*2))= ...
        (1-rou)*pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
end
    
%% 循环寻找最优路径
for kk=1:100
     
    %% 路径搜索
    [path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,...
        pheromone,HeightData,starty,starth,endy,endh); 
    
    %% 适应度值计算更新
    fitness=CacuFit(path);                               
    [newbestfitness,newbestindex]=min(fitness);     
    if newbestfitness<bestfitness
        bestfitness=newbestfitness;
        bestpath=path(newbestindex,:);
    end 
    BestFitness=[BestFitness;bestfitness];
    
    %% 更新信息素
    cfit=100/bestfitness;
    for i=2:PortGrid-1
        pheromone(i,bestpath(i*2-1),bestpath(i*2))=(1-rou)* ...
            pheromone(i,bestpath(i*2-1),bestpath(i*2))+rou*cfit;
    end
 
end

%% 最佳路径
for i=1:21
    a(i,1)=bestpath(i*2-1);
    a(i,2)=bestpath(i*2);
end
figure(1)
x=1:21;
y=1:21;
[x1,y1]=meshgrid(x,y);
mesh(x1,y1,HeightData)
axis([1,21,1,21,0,2000])
hold on
k=1:21;
plot3(k(1)',a(1,1)',a(1,2)'*200,'--o','LineWidth',2,...
                       'MarkerEdgeColor','k',...
                       'MarkerFaceColor','g',...
                       'MarkerSize',10)
plot3(k(21)',a(21,1)',a(21,2)'*200,'--o','LineWidth',2,...
                       'MarkerEdgeColor','k',...
                       'MarkerFaceColor','g',...
                       'MarkerSize',10)
                   text(k(1)',a(1,1)',a(1,2)'*200,'S');
text(k(21)',a(21,1)',a(21,2)'*200,'T');
xlabel('km','fontsize',12);
ylabel('km','fontsize',12);
zlabel('m','fontsize',12);
title('三维路径规划空间','fontsize',12)
set(gcf, 'Renderer', 'ZBuffer')
hold on
plot3(k',a(:,1)',a(:,2)'*200,'--o')

%% 适应度变化
figure(2)
plot(BestFitness)
title('最佳个体适应度变化趋势')
xlabel('迭代次数')
ylabel('适应度值')

function fitness=CacuFit(path)
%% 该函数用于计算个体适应度值
%path       input     路径
%fitness    input     路径

[n,m]=size(path);
for i=1:n
    fitness(i)=0;
    for j=2:m/2
        %适应度值为长度加高度
        fitness(i)=fitness(i)+sqrt(1+(path(i,j*2-1)-path(i,(j-1)*2-1))^2 ...
            +(path(i,j*2)-path(i,(j-1)*2))^2)+abs(path(i,j*2));
    end
End

function qfz=CacuQfz(Nexty,Nexth,Nowy,Nowh,endy,endh,abscissa,HeightData)
%% 该函数用于计算各点的启发值
%Nexty Nexth    input    下个点坐标
%Nowy Nowh      input    当前点坐标
%endy endh      input    终点坐标
%abscissa       input    横坐标
%HeightData     input    地图高度
%qfz            output   启发值

%% 判断下个点是否可达
if HeightData(Nexty,abscissa)<Nexth*200
    S=1;
else
    S=0;
end

%% 计算启发值
%D距离
D=50/(sqrt(1+(Nowh*0.2-Nexth*0.2)^2+(Nexty-Nowy)^2)+sqrt((21-abscissa)^2 ...
    +(endh*0.2-Nexth*0.2)^2+(endy-Nowy)^2));
%计算高度
M=30/abs(Nexth+1);
%计算启发值
qfz=S*M*D;



    

function [path,pheromone]=searchpath(PopNumber,LevelGrid,PortGrid,pheromone,HeightData,starty,starth,endy,endh)
%% 该函数用于蚂蚁蚁群算法的路径规划
%LevelGrid     input    横向划分格数
%PortGrid      input    纵向划分个数
%pheromone     input    信息素
%HeightData    input    地图高度
%starty starth input    开始点
%path          output   规划路径
%pheromone     output   信息素

%% 搜索参数
ycMax=2;   %蚂蚁横向最大变动
hcMax=2;   %蚂蚁纵向最大变动
decr=0.9;  %信息素衰减概率

%% 循环搜索路径
for ii=1:PopNumber
    
    path(ii,1:2)=[starty,starth];  %记录路径
    NowPoint=[starty,starth];      %当前坐标点
    
    %% 计算点适应度值
    for abscissa=2:PortGrid-1
        %计算所有数据点对应的适应度值
        kk=1;
        for i=-ycMax:ycMax
            for j=-hcMax:hcMax
                NextPoint(kk,:)=[NowPoint(1)+i,NowPoint(2)+j];
                if (NextPoint(kk,1)<20)&&(NextPoint(kk,1)>0)&&(NextPoint(kk,2)<20)&&(NextPoint(kk,2)>0)
                    qfz(kk)=CacuQfz(NextPoint(kk,1),NextPoint(kk,2),NowPoint(1),NowPoint(2),endy,endh,abscissa,HeightData);
                    qz(kk)=qfz(kk)*pheromone(abscissa,NextPoint(kk,1),NextPoint(kk,2));
                    kk=kk+1;
                else
                    qz(kk)=0;
                    kk=kk+1;
                end
            end
        end
        
        
        %选择下个点
        sumq=qz./sum(qz);
    
        pick=rand;
        while pick==0
            pick=rand;
        end
        
        for i=1:25
            pick=pick-sumq(i);
            if pick<=0
                index=i;
                break;
            end
        end
        
        oldpoint=NextPoint(index,:);
        
        %更新信息素
        pheromone(abscissa+1,oldpoint(1),oldpoint(2))=0.5*pheromone(abscissa+1,oldpoint(1),oldpoint(2));
        
        %路径保存
        path(ii,abscissa*2-1:abscissa*2)=[oldpoint(1),oldpoint(2)];    
        NowPoint=oldpoint;
        
    end
    path(ii,41:42)=[endy,endh];
end