FP-Tree的Python实现
一、问题的背景
给定一组商品购买信息,找到商品购买中频繁出现的商品集。比如说,我们有如下的商品交易信息:
| Tip | Items |
|---|---|
| 1 | Bread, Milk |
| 2 | Bread, Diaper, Beer, Egg |
| 3 | Milk, Diaper, Beer, Coke |
| 4 | Bread, Milk, Diaper, Beer |
| 5 | Bread, Milk, Diaper, Coke |
我们定义,Itemset 为一系列item的集合,比如:{Milk, Bread, Diaper};定义 k-itemset 为包含k个items的itemset;定义support 是所有交易信息中,包含这个 itemset 的子集。比如s({Milk, Bread, Diaper}) = 2/5;定义frequent Itemset 是一组itemset,它的support 大于等于minsup,这个minsup值由我们自己给定。
为了找出频繁项集,最直观的方法是我们罗列出所有的候选项,然后计算每个候选项的support,最后将满足要求的频繁项保存下来。比如说,我们有M个交易信息储存在数据库中,有N个候选项,那么我们必须要比较MN次,显然它的时间复杂度是非常大的。我们可以通过构建FP-Tree(Frenquent Pattern Tree)的方法,只在数据库中读取2次,就能将所有的重要信息存储在FP-tree中。FP-Tree是简洁的,被用来生成大型数据集。
二、FP-Tree的生成
1、删除不频繁出现的商品,并将每次交易的商品顺序按照出现频率重新排列
2、根据以上的数据建立FP-Tree
3、对于每一个item(或itemset),根据FP-Tree建立FP-Conditional Tree
4、决定频繁模式
比如说我们给定了如下数据集,TID是索引,商品类别用a, b, c, d等字母代替:
| TID | Items Bought |
|---|---|
| 100 | a, b, c, d, e, f, g, h |
| 200 | a, f, g |
| 300 | b, d, e, f, j |
| 400 | a, b, d, i, k |
| 500 | a, b, e, g |
我们首先扫描一次数据库,得到item的出现频率,结果如下:
| Item | Frenquency |
|---|---|
| a | 4 |
| b | 4 |
| c | 1 |
| d | 3 |
| e | 3 |
| f | 3 |
| g | 3 |
| h | 1 |
| i | 1 |
| j | 1 |
| k | 1 |
假设我们需要找的min support = 3,那么c, h ,i ,j, k显然无法成为频繁项集,因此我们可以将它们从考虑范围内移除,并将每次的交易信息按照出现频率由大到小排序,如果频率相同就按照字母顺序排列,得到以下的结果:
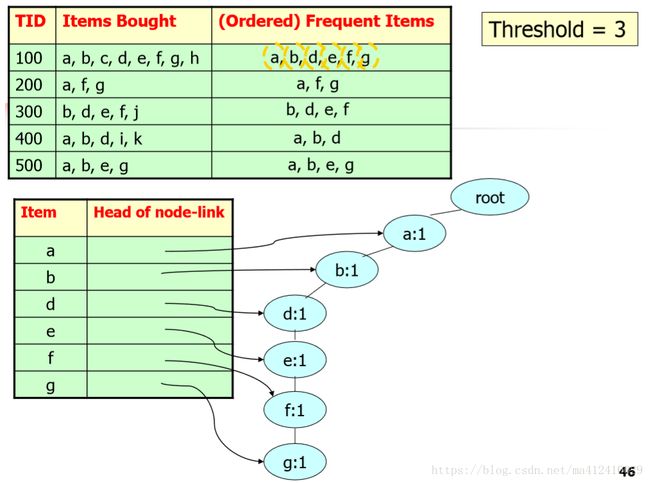
| TID | Items Bought | (Ordered)Frequent Items |
|---|---|---|
| 100 | a, b, c, d, e, f, g, h | a, b, d, e, f, g |
| 200 | a, f, g | a, f, g |
| 300 | b, d, e, f, j | b, d, e, f |
| 400 | a, b, d, i, k | a, b, d |
| 500 | a, b, e, g | a, b, e, g |
数据已经建立完成,我们接下来需要做的就是如何构建FP-Tree,首先创建树的根节点,用‘null’或者‘root’标记。并对每一次的交易信息创建一个分支,比如说第一个交易信息包含:a,b,d,e,f,g六项,导致树的第一个分支包含6个节点,其中a作为根的子女链接到根,b链接到a,d链接到e,f连接到e,g链接到f。第二个交易信息,包含a,f,g三项,该分支与第一个分支共享前缀a,由于共享,我们将a的计数增加1,之后创建新的节点f连接到a,创建新的节点g,链接到f。当一次交易信息考虑增加分支时,沿共同前缀上的每个节点的计数增加1,为前缀之后的项创建节点和链接。
为了方便树的遍历,创建一个项头表,使每项通过一个结点链向指向它在树中的位置。扫描所有的交易后得到的树显示如下。
这样,数据库挖掘频繁模式的挖掘问题转换成了挖掘FP树的问题。
三、FP树的挖掘
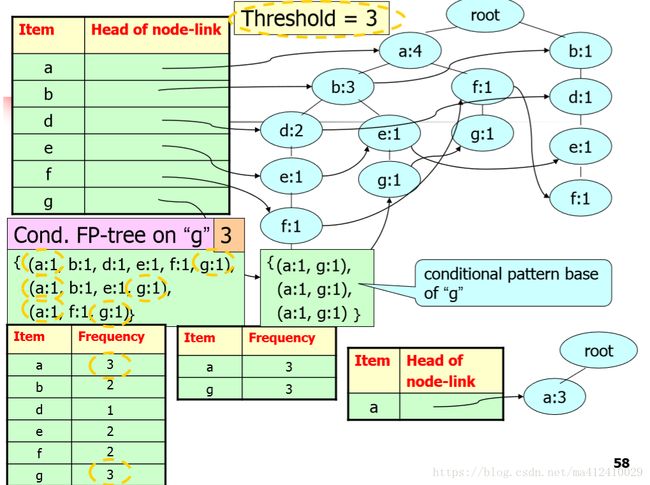
FP树的挖掘由长度为1的频繁模式开始,构造它的条件模式基(一个“子数据库”,由FP树中与该后缀模式一同出现的前缀路径集组成)。然后构造条件FP树,并递归地在该树上进行挖掘。比如说我们已经有了如下的FP-Tree,我们对项头表中的每一项,按照support由低到高的顺序,依次进行挖掘。比如说挖掘以g为后缀的条件模式基,由于我们已经有了项头表,我们可以很轻易的找到树中所有g的位置,并依次向上搜索,直到到达root。因此我们得到了一下三个以g为后缀的交易信息:{a:1,b:1,d:1,e:1,g:1},{a:1,b:1,e:1,g:1},{a:1,f:1,g:1},这三条就是我们得到的条件模式基。条件模式基中的每一条交易信息的support以交易信息中每一项的最小support作为该条交易信息的support。比如说我们得到的是{a:4,f:1,g:1},但是因为g只出现了1次,所以最后的统计为{a:1,f:1,g:1}。根据条件模式基,我们同样可以以次作为新的数据,删除掉出现次数不频繁(小于min support的项,并将交易信息按照在条件模式基中的出现频率排序)构建g的FP-条件树。由于g在每个条件模式基中都出现了,我们不必考虑它。从构造的结果来看,只有a的support >= minsupport,因此我们可以得到频发模式为{g},{g,a}。
四、FP-Tree的完整算法
| 算法:FP-Growth 使用FP树,通过模式增长挖掘频繁模式。 输入: 1、D:事务数据库 2、min_support:最小支持度阈值 输出:频繁模式的完全集 方法: 1、按以下步骤构造FP树: (a)扫描事务数据库D一次。收集频繁项的集合F和它们的支持度计数。对F按支持度计数降序排序,结果为频繁项列表L (b)创建FP树的根节点,以‘null’或‘root’标记它,对于D中每个事务Trans,执行: 选择Trans中的频繁项,并按L中的次序排序。设Trans排序后的频繁项列表为[p|P],其中p是第一个元素,而P是剩余元素 的列表。调用insert_tree([p|P],T)。该过程执行情况如下。如果T有子女N使得N.item_name = p.item_name,则N的计数 增加1;否则,创建一个新结点N,将其计数设置为1,链接到它的父节点T,并且通过结点链结构将其链接到具有相同 item_name的结点。如果P非空,则递归调用insert_tree(P,N)。 2、FP树的挖掘通过调用FP_growth(FP_tree,null)实现。该过程如下。 procedure FP_growth(Tree,α) (1)if Tree包含单个路径P then (2)for 路径P中结点的每个支持组合(记作β) (3)产生模式βUα,其支持度计数support_count 等于β中结点的最小支持度计数 (4)else for Tree 的头表中的每个ai{ (5)产生一个模式β=aiUα,其支持度计数support_count = ai*support_count (6)构造β的条件模式基,然后构造β的条件FP树Treeβ (7)if Treeβ非空 then (8)调用FP_growth(Treeβ,β)} |
五、FP-Tree的Python实现
import re
import collections
import itertools
data = []
data = [['a','b','c','d','e','f','g','h'],['a','f','g'],['b','d','e','f','j'],['a','b','d','i','k'],['a','b','e','g'],['g','b']]
#print(data)
data = data
support = 3
#统计item的频率
CountItem = collections.defaultdict(int)
for line in data:
for item in line:
CountItem[item] += 1
#将dict按照频率从大到小排序,并且删除掉频率过小的项
a = sorted(CountItem.items(),key = lambda x:x[1],reverse=True)
for i in range(len(a)):
if a[i][1] < support:
a = a[:i]
break
#更新data中,每一笔交易的商品顺序
for i in range(len(data)):
data[i] = [char for char in data[i] if CountItem[char] >= support]
data[i] = sorted(data[i],key = lambda x:CountItem[x],reverse=True)
#定义好节点
class node:
def __init__(self,val,char):
self.val = val#用于定义当前的计数
self.char = char#用于定义当前的字符是多少
self.children = {}#用于存储孩子
self.next = None#用于链表,链接到另一个孩子处
self.father = None#构建条件树时向上搜索
self.visit = 0#用于链表的时候观察是否已经被访问过了
self.nodelink = collections.defaultdict()
self.nodelink1 = collections.defaultdict()
class FPTree():
def __init__(self):
self.root = node(-1,'root')
self.FrequentItem = collections.defaultdict(int)#用来存储频繁项集
self.res = []
def BuildTree(self,data):#建立fp树的函数,data应该以list[list[]]的形式,其中内部的list包含了商品的名称,以字符串表示
for line in data:#取出第一个list,用line来表示
root = self.root
for item in line:#对于列表中的每一项
if item not in root.children.keys():#如果item不在dict中
root.children[item] = node(1,item)#创建一个新的节点
root.children[item].father = root#用于从下往上寻找
else:
root.children[item].val += 1#否则,计数加1
root = root.children[item]#往下走一步
#根据这个root创建链表
if item in self.root.nodelink.keys():#如果这个item在nodelink中已经存在了
if root.visit == 0:#如果这个点没有被访问过
self.root.nodelink1[item].next = root
self.root.nodelink1[item] = self.root.nodelink1[item].next
root.visit = 1#被访问了
else:#如果这个item在nodelink中不存在
self.root.nodelink[item] = root
self.root.nodelink1[item] = root
root.visit = 1
print('树建立完成')
return self.root
def IsSinglePath(self,root):
#print('是否为单路径')
if not root:
return True
if not root.children: return True
a = list(root.children.values())
if len(a) > 1: return False
else:
for value in root.children.values():
if self.IsSinglePath(value) == False: return False
return True
def FP_growth(self,Tree,a,HeadTable):#Tree表示树的根节点,a用列表表示的频繁项集,HeadTable用来表示头表
#我们首先需要判断这个树是不是单路径的,创建一个单路径函数IsSinglePath(root)
if self.IsSinglePath(Tree):#如果是单路径的
#对于路径中的每个组合,记作b,产生模式,b并a,support = b中节点的最小支持度
root, temp = Tree, []#创建一个空列表来存储
while root.children:
for child in root.children.values():
temp.append((child.char,child.val))
root = child
#产生每个组合
ans = []
for i in range(1,len(temp)+1):
ans += list(itertools.combinations(temp,i))
#print('ans = ',ans)
for item in ans:
mychar = [char[0] for char in item] + a
mycount = min([count[1] for count in item])
if mycount >= support:
#print([mychar,mycount])
self.res.append([mychar,mycount])
#print(self.res)
else:#不是单路径,存在多个路径
root = Tree
#print(Tree.char)
#对于root头表中的每一项进行操作
HeadTable.reverse()#首先将头表逆序
for (child,count) in HeadTable:#child表示字符,count表示支持度
b = [child] + a #新的频繁模式
#构造b的条件模式基
#print(b)
self.res.append([b,count])
tmp = Tree.nodelink[child]#此时为第一个节点从这个节点开始找,tmp一直保持在链表当中
data = []#用来保存条件模式基
#if b == ['sausage','cream']:
# print(root.char)
while tmp:#当tmp一直存在的时候
tmpup = tmp#准备向上走
res = [[],tmpup.val]#用来保存条件模式
while tmpup.father:
res[0].append(tmpup.char)
tmpup = tmpup.father
res[0] = res[0][::-1]#逆序
data.append(res)#条件模式基保存完毕
tmp = tmp.next
#if b == ['sausage','cream']: print(2)
#条件模式基构造完毕,储存在data中,下一步是建立b的fp-Tree
#统计词频
CountItem = collections.defaultdict(int)
for [tmp,count] in data:
for i in tmp[:-1]:
CountItem[i] += count
for i in range(len(data)):
data[i][0] = [char for char in data[i][0] if CountItem[char] >= support]#删除掉不符合的项
data[i][0] = sorted(data[i][0],key = lambda x:CountItem[x],reverse=True)#排序
#print('2',data)
#此时数据已经准备好了,我们需要做的就是构造条件树
#CountItem1 = collections.defaultdict(int)
root = node(-1,'root')#创建根节点,值为-1,字符为root
for [tmp,count] in data:#item 是 [list[],count] 的形式
tmproot = root#定位到根节点
for item in tmp:#对于tmp中的每一个商品
#print('123',item)
#CountItem1[item] += 1
if item in tmproot.children.keys():#如果这个商品已经在tmproot的孩子中了
tmproot.children[item].val += count#更新值
else:#如果这个商品没有在tmproot的孩子中
tmproot.children[item] = node(count,item)#创建一个新的节点
tmproot.children[item].father = tmproot#方便从下往上找
tmproot = tmproot.children[item]#往下走一步
#根据这个root创建链表
if item in root.nodelink.keys():#这个item在nodelink中存在
if tmproot.visit == 0:
root.nodelink1[item].next = tmproot
root.nodelink1[item] = root.nodelink1[item].next
tmproot.visit = 1
else:#这个item在nodelink中不存在
root.nodelink[item] = tmproot
root.nodelink1[item] = tmproot
tmproot.visit = 1
if root:#如果新的条件树不为空
NewHeadTable = sorted(CountItem.items(),key = lambda x:x[1],reverse=True)
for i in range(len(NewHeadTable)):
if NewHeadTable[i][1] < support:
NewHeadTable = NewHeadTable[:i]
break
self.FP_growth(root,b,NewHeadTable)#我们需要创建新的headtable
#return root#成功返回条件树
def PrintTree(self,root):#层次遍历打印树
if not root: return
res = []
if root.children:
for (name,child) in root.children.items():
res += [name+' '+str(child.val),self.PrintTree(child)]
return res
else: return
obj = FPTree()
root = obj.BuildTree(data)
#print(obj.PrintTree(root))
obj.FP_growth(root,[],a)
print(obj.res)