一、为什么前端需要学习数据结构与算法?
以前的前端页面都是多页面,现在前端的趋势是单页面应用,需要将复杂的逻辑都放在前端实现,需要考虑到运行效率的问题,因此我们需要学会选择正确的数据结构和算法。例如,邮件应用查询功能,要在几千条数据中查找目标数据,如果选择的数据结构和算法不正确,会导致运行时间很长,影响用户体验。
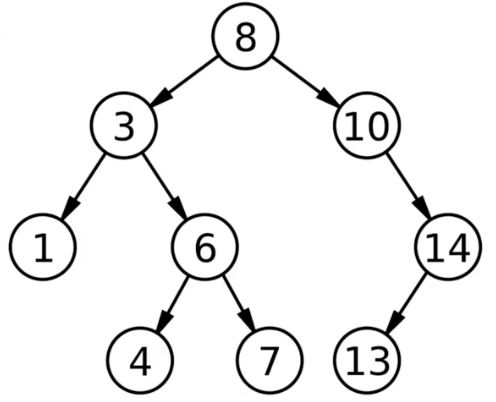
二、二叉树相关概念
- 根节点
- 兄弟节点
- 叶子节点
- 中间节点
- 树的层次
- 树的高(important!):树的层次树。
- 结点的度:结点子树的个数。
- 树的度:树中最大的结点度。
- 排序二叉树:又称二叉查找树,亦称二叉搜索树。左子树上所有结点的值均≤根结点的值,右子树上所有结点的值均≥根结点的值。
三、二叉树的遍历
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
1.先序遍历
中左右
- 递归法
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
- 非递归法
- 先将头结点head入栈;
- 只要栈不为空,就弹出栈顶,并打印;然后判断其是否有左右子树,有的话就入栈;因为栈是先进后出,因此右子树先入栈,再左子树入栈。
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack stack = new Stack();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
2.中序遍历
左中右
- 递归法
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
- 非递归法
依次打印左边界,但是是按照逆序的方式。
- 先将head入栈
- 用一个指针,先指向head的左子树,head不为空,就将其入栈,head为空就弹出打印,head向当前节点的右子树移动。
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack stack = new Stack();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
3.后序遍历
左右中
- 递归法
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
- 非递归法
与先序遍历一样,先序遍历是先压中,出压栈顺序是先压右再压左。后序遍历就是先压中,出压栈顺序是先压左再压右,本来顺序是右左中,打印的时候就借助一个辅助栈,进行逆序打印就行了。
public static void posOrderUnRecur1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack s1 = new Stack();
Stack s2 = new Stack();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
4.折纸问题
【题目】请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。给定一个输入参数N,代表纸条都从下边向上方连续对折N次,请从上到下打印所有折痕的方向。
例如:N=1时,打印:
down
N=2时,打印:
down
down
up
【解题思路】将每次的折痕进行序号标记,得到规律,左子树的头结点是下,右子树的头结点是上,根节点是下,整个顺序就是树的中序遍历。
5.在二叉树中找到一个节点的后继节点
【题目】现在有一种新的二叉树节点类型如下:
public class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data) {
this.value = data;
}
}
【一些概念】
后继节点:节点在中序遍历序列中的后一个节点。
【解题思路】
- 中序遍历是左中右
- 一个节点如果有右子树,那么它的后继节点就是右子树的最左的节点(从该节点向其左子树进行查找,直到为空为止,不包括右子树的左节点!)。
- 一个节点如果没有右子树,就寻找它的父节点以及父节点的父节点...直到父节点是一个节点的左子树,那么该节点的父节点就是它的后继节点。