仔细研究历年研究生数学建模比赛出题的类型,就会发现,几乎年年在考有关飞行器,无人机这样的问题,因此,有必要好好将这一类题目做一个总结归纳。
2018年研究生数学建模E题目:《多无人机对组网雷达的协同干扰》
基本概念
18年E题目是有关多无人机协同干扰组网雷达的问题,光题目说明就有一两千字,题目确实比较复杂。
认真阅读上下文后,可以大致理解题设场景和基本要求。所有的问题都基于一个同源干扰的概念展开。
无人机如何干扰雷达?
要理解同源干扰,首先要理解一架无人机是如何干扰一台雷达的。
简单来说,就是雷达与无人机共线,无人机会通过反射信号使得雷达误以为在其延长线上会存在一个点,并将这个点当作检测到的敌机,该点称之为虚假目标点。“虚假”二字表明了这个点是干扰产生的。
如何骗过组网雷达?
在电子对抗领域,侦察敌机的入侵绝对不可能仅凭一台雷达来做判断。为了避免 “无人机-雷达” 这种一对一干扰造成误判,产生了同源检验技术。即在同一时刻,多架无人机分别干扰组网雷达中的某一台雷达,这样就会产生多个虚假目标点。假如这多个虚假目标点中,至少有三个是在同一个位置时,就断定这个点是一个真实的点,是由敌机产生的。这样就相当于骗过了组网雷达。
什么是虚假航迹点?
组网雷达每个时刻都会做同源干扰检测,如果在各个时刻,无人机都可以骗过组网,产生对应的虚假目标点,那么这些虚假目标点就可以看作是由真实的敌机产生的飞行轨迹,亦即虚假航迹点。
无人机协同干扰怎么理解?
所谓的无人机协同干扰,就是给定一个虚假航迹(每个时刻下的空间坐标),要求结合雷达探测范围、无人机飞行限制条件(如飞行速度,飞行高度等),合理安排多架无人机飞行(每个时刻下应该飞到哪个空间位置),使它们在每个时刻下,都可以骗过组网雷达(即每个时刻的虚假航迹点都是可以通过同源检验的),这样就表示无人机通过协同干扰雷达,使得对方的组网雷达检测到有异常的敌机飞行轨迹,惊扰到对方,使之产生混乱,进而获得有利战机。
已知条件
对于本题目的中的三个问题来说,都遵循一些基本的已知条件:
- 假目标的形成满足距离欺骗原理
- 航迹点形成满足同源检验原理
- 5个雷达坐标给定
- 无人机的飞行参数给定:航速:120km ~ 180km/h ,飞行高度:2000m ~ 2500m,飞行间距:100m以上,最大加速度:不超过10 米每二次方秒
- 雷达探测范围:150km
- 雷达每 10s 更新一批航迹点
问题场景演示
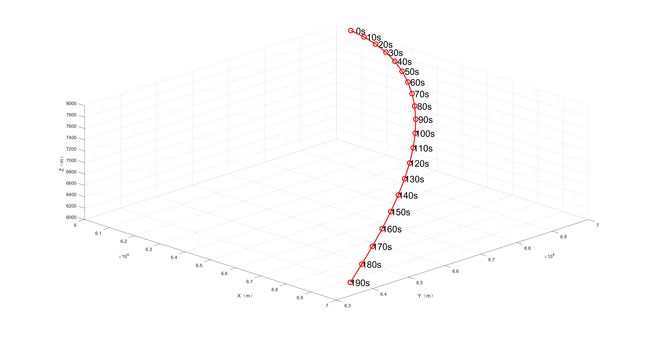
根据题目给的行航迹点坐标,则空间的飞行轨迹如图所示:
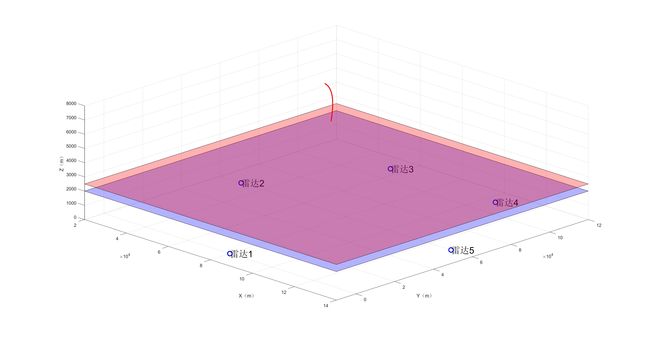
雷达的空间相对位置如图:
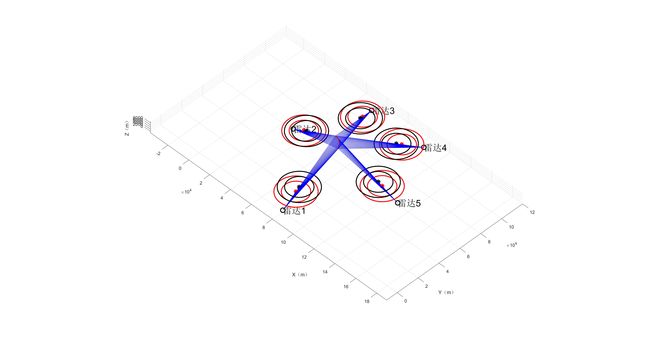
所有问题围绕这样一个场景来展开,给定5个雷达,给定任意架数的无人机,令其在飞行参数范围下,在2000m ~ 2500m高空范围下,进行组网雷达干扰,生成所设定的航迹,如图所示:
无人机空间坐标解算
根据题目有关无人机距离欺骗干扰雷达的原理,当干扰成功时,‘’雷达-无人机-假目标点“三者在一条直线上。如下图所示:
根据三角形相似原理,雷达、无人机、航迹点三者的坐标将满足如下关系式(注意观察红色线条及其相关的线段):
\[ \frac{z_a-z_r}{z_o-z_r}=\frac{x_a-x_r}{x_o-x_r}=\frac{y_a-y_r}{y_o-y_r} \]
于是当 $ z_a$ 给定时,便可以解算出对应的无人机空间坐标:
\[ \left\{ \begin{array}{c} x_a=\frac{z_a-z_r}{z_o-z_r}\cdot \left( x_o-x_r \right) +x_r\\ y_a=\frac{z_a-z_r}{z_o-z_r}\cdot \left( y_o-y_r \right) +y_r\\ z_a=z_a\\ \end{array} \right. \]
无人机飞行能力分析
根据无人机飞行参数的规定,飞行速度范围在120km/h ~ 180km/h(换算后为33.33m/s ~ 50m/s),在给定的航迹飞行时间范围下,无人机能够飞到的最远距离可以轻松地计算出来,我们称这样的计算过程为“无人机飞行能力分析”。
在问题一中,无人机飞行时间为20个航迹点时间,时间间隔为10s,共飞行190s,则无人机在速度和时间约束下,能够飞到的最远距离为 (33.33 ~ 50)*190 = (6332.7 ~ 9500)m。对于不同的飞行高度,取两个极端值,2000m高(红色)度和2500m高度(黑色),同色的两个圆表示最小、最大距离。画出示意图:
在问题二三中,飞行时间为5分钟,即飞行300s,生成31个航迹点,能够飞到的最远距离为 (33.33 ~ 50)*300 = (9999 ~ 15000)m,同样的画出示意图:
飞行能力重要结论
很明显,不管无人机怎么飞行,一旦确定干扰某一雷达后,就只可能继续干扰该雷达,不能够飞离该片区域去干扰别的雷达(要干扰雷达,就需要飞到雷达与航迹点的连线上,即图中蓝色的连线)。
这个结论非常的重要!!因为有了这个结论后,一架无人机就只负责干扰一台雷达,问题得到简化。
无人机干扰能力分析
由无人机飞行能力分析,我们可以确定雷达的干扰模式为一对一持续干扰模式。这样我们就可以单独去考虑每一台雷达的干扰情况了。对于一个雷达来说,在20个航迹点时间下,无人机要对其造成干扰,则一定出现在雷达与行航迹点连线上,如下图所示(以2000m高度为例):
图中红色的的为解算出的20个时刻下无人机的飞行点位,将其俯视图画出,如图所示:
20个时刻,对应于20个飞行点位,而这20个飞行点位,由多架无人机协同产生。也就是说,每个时刻的点位将会分配给不同的无人机去实现覆盖,即在对应时间下,飞往对应位置实现该时刻的雷达干扰任务。那么无人机干扰雷达的能力怎么分析?换句话说,一架无人机能够在其飞行过程中,实现几个飞行点位的覆盖?
这个问题,需要结合飞行参数,以及飞行时间来计算飞行点位是否落在无人机各时刻飞行距离范围内,能够落在范围内,则表示点位覆盖任务能够完成,否则不能。
干扰能力重要结论
通过上面的点位路径可以很明显的看出,所有点并不在一条直线上,所以若无人机仅作直线飞行的话,最多覆盖两个点,绝对不可能覆盖到第三个点,这个结论也十分重要,问题又得到了进一步化简。
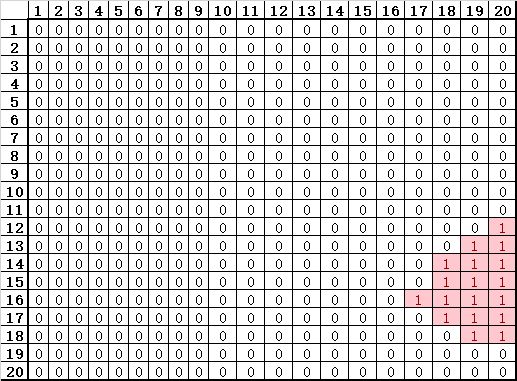
点位覆盖判断矩阵
这个问题很好计算,首先计算出这20个飞行点位两两之间的距离,而这两两之间的点位,时间间隔也可以表达出来,乘以飞行速度范围后,得到一个距离区间,判断是否落在区间,若落在区间则将两个点位对应的序号作为行列,记作1,反之则记作0。这样就可以得到一个20*20的点位覆盖判断矩阵。
可以看到,2000m飞行高度下能覆盖的点位比较少。并且集中在最后几个时刻点,最后几个时刻相对来说能够被覆盖的点位更多,这个是普遍规律。
最少无人机协同策略
对于上述点位覆盖矩阵,我们需要做的是,使用最少的无人机协同完成点位覆盖任务。根据上述普遍规律,我们从大号开始找,当存在不为0的行时,以最小行号取出,并记录下来,将对应列抹零,继续判断。当找到的全是0时,则需要增派无人机。最终将会以最少的无人机实现20个点位覆盖。通过该策略可以得到如下无人机协同飞行路径规划表(以上面的矩阵为例):
| 起始点位 | 终到点位 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | 10 |
| 11 | 11 |
| 12 | 20 |
| 13 | 19 |
| 14 | 18 |
| 15 | 15 |
| 16 | 17 |
其中起始点位与终到点位相同的,表示改点位无法与其他点位在一次飞行中覆盖到,需要增派无人机单独覆盖。可见此时至少需要16架无人机完成2000m高度下对雷达1的干扰任务。
无人机各时刻飞行点位按速度解算
根据上面的分析,可以计算出无人机起始和终到点位,而题目要求最终结果要给出每架无人机的各时刻空间坐标。因此我们只需要按照起始终到点位,以及时间间隔重新解算飞行速度,再根据飞行方向(起始与终到点位连线即为方向),将速度分解到各个坐标轴方向,计算分速度,再计算起始点位之前以及之后的各个点位的空间坐标即可。
问题一的解答
前面讲述了对于一台雷达的干扰问题,而对于多雷达的同源检验,其实是一个可行解组合问题。对于每一个雷达,都可以解算出,至少需要多少架无人机来完成干扰任务。针对每一台雷达,对2000m ~ 2500m高空进行遍历求解,可以得到无人机需求变化。
观察曲线变化规律,就可以发现,雷达1和雷达5最难实现干扰,在2000m ~ 2500m高度变化下,无人机始终要派出较多数量,并且大部分都支持一个点位覆盖,效率非常低下。而对于雷达2、雷达3、雷达4来说,无人机派出数量和增派数量在2450m高空及以上时,需求数量较少。因此假如要以最少无人机去实现同源检验,完成航迹点生成任务,就可以只干扰雷达2、雷达3、雷达4。需要的最少数量为 10 + 10 + 11 = 31 架无人机。其中干扰雷达2、雷达3的无人机均可实现2个点位覆盖,干扰雷达4的无人机,有9架可实现2个点位覆盖,另外2架需要增派,仅覆盖一个点位。
其实这个结果也符合实际情况,因为在相对位置上,雷达2、雷达3、雷达4更靠近航迹,而雷达1、雷达5相对较远。
未完待续...
我太难了!!