穷人的语义处理工具箱之二:语义编辑距离
author: 张俊林
语义编辑距离其实是去年和语义Jaccard一起做的,这篇文章主体内容也是去年写的。之所以现在才看到,说明我手上的存货文章几乎见底了,否则也许这篇很久以后才会发出来。一般我手上会写出后攒着几篇作为存货,这是为了尽量做到周更,避免没精力写的时候手上没货以作备用。最近一个多月写东西的动力急剧衰减,所以没有写任何新的文章,只能陆续用存货来救场,可见持之以恒地做一件费力又没有明显收益的事情确实是挺不容易的,不过今年尽量还是能够做到每周一更,也算是对自己的一种锻炼。
为什么这里我们说是穷人的语义处理工具箱?在“穷人的语义处理工具箱之一:语义版Jaccard”一文开头我们说明了原因,此处就不再赘述。我们直接进入主题。
|编辑距离(Edit Distance)
编辑距离由俄罗斯科学家Vladimir Levenshtein提出,所以编辑距离也被称为Levenshtein距离。这是一种很常用的计算两个字符串相似性的度量工具。它的具体含义是指把一个字符串转换为另一个字符串所需要的最小编辑次数,这里的“编辑”一般包含三种操作:插入一个字符、删除一个字符以及将某个字符替换成另外一个字符。假设每种操作的代价都是1,那么把一个字符串通过上述三种操作不断变换,直到转为另外一个字符串的最小编辑操作次数n就是编辑距离:n。
比如假设我们现在手头有两个字符串:edit和red,那么通过下列操作来将edit转换为red:
Step1:edit->redit (插入r)
Step 2:redit->redt (删除i)
Step 3:redt->red (删除t)
总共做了三次操作,假设每种操作代价是相同的,都是1,那么edit和red的编辑距离是3。
编辑距离是动态规划的一个典型实例,假设给定了要比较的两个字符串a和b,我们定义:
EditDistance(i,j):字符串a的长度为i的子串(即a中由第1个字符到第i个字符构成的子串)和字符串b长度为j的子串(即b中由第1个字符到第j个字符构成的子串)的编辑距离。
那么可以递归定义编辑距离如下:
初始状态1:
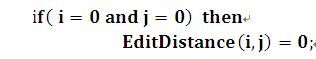
意思是:如果两个子串长度都为0,那么它们的编辑距离为0,这个好理解。
初始状态2:
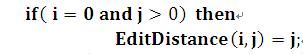
意思是:如果a句子的子串长度为0而b句子的子串长度不为0,那么它们的编辑距离为b句子的子串长度,这个也很好理解,因为要把a句子子串替换为b句子子串,那么只要不断插入b句子子串的j个字符就行。
初始状态3:
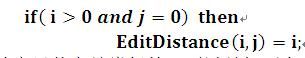
这个和初始状态2的意思其实是类似的,不过是把两个子串对调一下位置。它的意思是:如果 b句子的子串长度为0而a句子的子串长度不为0,那么它们的编辑距离为a句子的子串长度,这个同样也很好理解,因为要把a句子子串替换为b句子子串,那么只要不断删除a句子子串的i个字符就行。
递归状态:
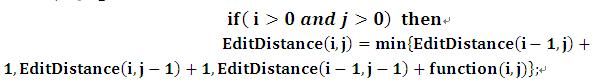
如果两个子串长度都不为0,那么需要考虑如下三种情况,并取其编辑距离最小值:
情况1:
意思是:假设我们已经知道a句子从第一个字符到第i-1个字符这个子串同b句子的前j个字符构成的子串的编辑距离,也就是假设EditDistance(i-1,j)已知,那么这种情形下两个子串的编辑距离EditDistance(i,j)为EditDistance(i-1,j)加上1。这个其实也好理解,因为在知道EditDistance(i-1,j)的情况下,要想知道EditDistance(i,j),只需要把a句子前i个字符构成的子串中把第i个字符删掉,那么就转换成了EditDistance(i-1,j)需要解决的问题了,因为EditDistance(i-1,j)已知,所以在这个基础上加上一次删除字符的代价1,就得到了EditDistance(i,j)。
情况2:
意思是:假设我们已经知道b句子从第一个字符到第j-1个字符这个子串同a句子的前i个字符构成的子串的编辑距离,也就是假设EditDistance(i,j-1)已知,那么这种情形下两个子串的编辑距离EditDistance(i,j)为EditDistance(i,j-1)加上1。这个同样也好理解,因为在知道EditDistance(i,j-1)的情况下,要想知道EditDistance(i,j),只需要把b句子前j个字符构成的子串中把第j个字符删掉,那么就转换成了EditDistance(i,j-1)需要解决的问题了,因为EditDistance(i,j-1)已知,所以在这个基础上加上一次删除字符的代价1,就得到了EditDistance(i,j)。
情况3:
意思是:假设我们已经知道a句子从第一个字符到第i-1个字符这个子串同b句子的第1个字符到第j-1个字符构成的子串的编辑距离,也就是假设EditDistance(i-1,j-1)已知,那么这种情况下两个子串的编辑距离EditDistance(i,j)为EditDistance(i-1,j-1)加上一个函数function(i,j)的值,这个函数定义如下:
这个也好理解,因为在EditDistance(i-1,j-1)已经知道的情形下,很明显,如果a句子第i个字符和b 句子的第j个字符相同,那么什么也不需要做就能使得两个子串保持相同,所以EditDistance(i,j)就是EditDistance(i-1,j-1)加上代价0;那么如果a句子第i个字符和b 句子的第j个字符不同,怎么才能最快捷地把EditDistance(i,j)转换为EditDistance(i-1,j-1)呢?很明显只要做一次替换操作,就是把a句子第i个字符替换成b 句子的第j个字符,就能最快地把EditDistance(i,j)问题转换为EditDistance(i-1,j-1)的问题,此时两个子串编辑距离是EditDistance(i-1,j-1)+1,因为做了一次替换操作。为什么替换操作是最快捷的?虽然你也可以先删除一个字符再插入一个字符来进行转换,但是这样做的代价是2,比替换一次的代价1要高,所以很明显替换操作是最合算的。
这里先提示一下:重点在于这个function(i,j)函数,因为后面我们对编辑距离进行语义版本改造,核心点就在这里。提示了这一点我想很多同学已经知道该怎么办了。
有了前面三个初始状态定义,再加上后面的递归定义,那么对于给定的两个句子,我们就可以从两个子串长度为0开始不断递归来推导这两个句子的编辑距离了。
一般实现的时候可以考虑构造矩阵来做。我们还是用刚开始给的例子edit和red来说明。
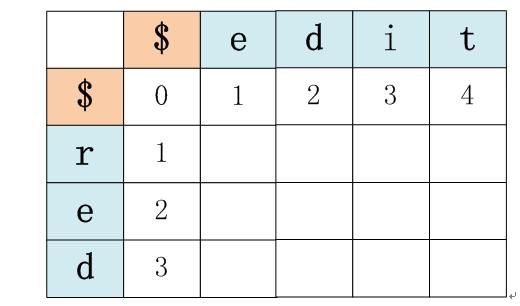
如果要计算edit和red的编辑距离,首先我们构造如下矩阵:
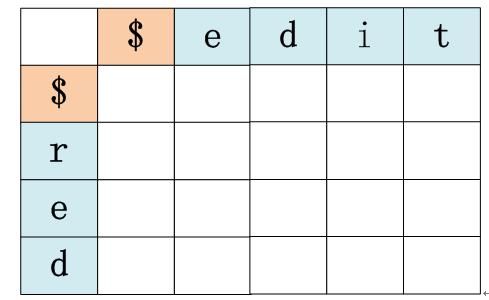
每个字符串我们增加了一个起始标记字符$,因为我们要计算三个初始状态,这里面需要能够表达子串长度为0的情况,那么就用句子起始标记符$来表征这种情形。对于初始状态1来说,就是计算矩阵中横坐标和纵坐标对应都是$符号处的矩阵值,可知其为0;对于初始状态2来说,我们假设red为a句子,edit为b句子,那么此时纵坐标为$符号那一行就代表了句子a子串长度为0,而句子b子串中的j取不同值的情况,可以依次填充对应的值;同理,对于初始状态3来说,横坐标为$符号那一列代表了句子b的子串长度为0,而句子a子串中的i取不同值的情况,也可以根据公式依次填充对应的值。于是我们把三个初始状态算完,就得到如下矩阵:
接下来就可以根据递归状态依次填充矩阵中其它空余值了,其实如果理解了递归状态的三种情形与矩阵中不同位置之间的对应位置关系,那么完全可以很快通过心算把上面的矩阵空余值填完。
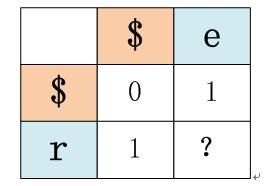
依然遵循上面假设,即a句子为red,b句子为edit,我们假设现在要计算EditDistance(1,1)的值,也就是下列子图中问号处的值:
要搞清楚下面一点:
问号上方的那个1代表了EditDistance(0,1)的值,就是a句子子串长度为0,b句子子串长度为1的编辑距离值,这个刚才已经算好了,由EditDistance(0,1)来推导EditDistance(1,1),这就是递归状态的情形1,那么此时EditDistance(1,1)= EditDistance(0,1)+1,所以得出1+1=2;
问号左边那个1代表了EditDistance(1,0)的值,就是a句子子串长度为1,b句子子串长度为0的编辑距离值,这个刚才也已经算好了,由EditDistance(1,0)来推导EditDistance(1,1),这就是递归状态的情形2,那么此时EditDistance(1,1)= EditDistance(1,0)+1,所以得出1+1=2;
问号左上方的那个0代表EditDistance(0,0)的值,就是a句子子串长度为0,b句子子串长度为0的编辑距离值,这个刚才也已经算好了,由EditDistance(0,0)来推导EditDistance(1,1),这就是递归状态的情形3,此时需要function(i,j)函数的介入,在目前的例子里就是function(1,1),意思是要判断字符r和字符e的情况,因为两者不同,所以function(1,1)取值为1,意思是要做替换操作其代价为1,那么此时EditDistance(1,1)=EditDistance(0,0)+function(1,1)=0+1=1;
上面三种情形得出的值分别是{2,2,1},取其最小值1,这就是问号处要填的内容,也就是EditDistance(1,1)对应的编辑距离。
稍微推广一下,就可以知道要计算矩阵中EditDistance(i,j)的值,那么矩阵中这个位置上方格子对应的是已经算好的EditDistance(i-1,j)的值,将其值加上1就是情形1推导出的EditDistance(i,j)的值;矩阵中这个位置左方格子对应的是已经算好的EditDistance(i,j-1)的值,将其值加上1就是情形2推导出的EditDistance(i,j)的值;而其左上方格子的值对应的是EditDistance(i-1,j-1)的编辑距离,此时需要判断横坐标和纵坐标对应字符是否相同,如果不同则代价加上1得出EditDistance(i,j)的值,如果相同,则EditDistance(i-1,j-1)+0则为EditDistance(i,j)的值。有了这个概念,后面的内容完全靠心算就可以很快填充完整个矩阵。其含义如下图所示:
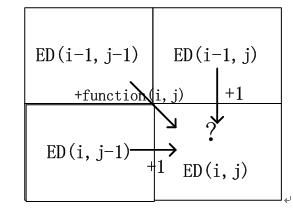
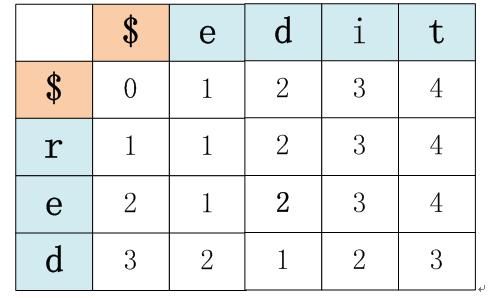
而整个矩阵最右下角的格子值就代表了两个句子a和b的整体的编辑距离,所以填充完的矩阵值如下:
也就是说,edit和red的编辑距离是矩阵右下角格子的值3。
上面举的例子都是英文,其实对中文,处理起来也是完全一样的,无非是把一个中文汉字看做一个英文字符即可。
|语义版编辑距离(Semantic Edit Distance)
现在我们进入正题的正题,就是语义编辑距离如何计算。提出语义版编辑距离的出发点和本系列第一篇文章语义Jaccard的出发点是一致的,就是编辑距离作为衡量字符串距离远近的度量函数,它有个缺点,只能判断字符串的字面匹配的相同程度,而不能判断语义级别的语义相似程度。
比如两个句子分别为:
SentenceA:电脑多少钱
SentenceB:计算机价格
如果按照经典编辑距离计算的话,假设我们以汉字为单位,可以得出其编辑距离如下图:
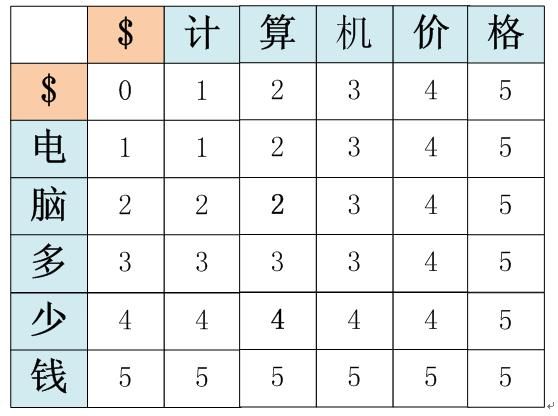
也就是说两个句子的编辑距离为5。
但是很明显这两个句子基本语义等价,然而从编辑距离的计算过程是完全无法体现这一点的,那么能否对经典编辑距离进行改造,把这种语义匹配考虑进去呢?
当然可以!
语义版编辑距离整个计算过程和经典编辑距离计算过程基本完全一样,只需要对原有计算流程做一点整容小手术,那就是递归过程中情形3中的function(i,j)函数。
Function(i,j)的本意是判断两个句子中第i个字符和第j个字符,如果相等则其值为0,如果不相同则其值为1。很明显这是一种字面匹配,而只要我们把这个函数改造成能够体现语义的计算,那么就可以把传统的编辑距离改造成语义版的编辑距离。
我们把这个函数整容成下面的形式:
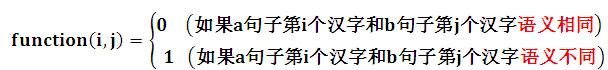
那么怎么判断两个汉字是否语义相同呢?同样地,在这里可以引入汉字的Word Embedding,这是一种在一定程度上代表汉字语义的低维向量表示,可以通过Word2Vec工具无监督地学习获得,只要我们在function(i,j)中引入两个汉字Word Embedding通过Cosine计算的语义相似性,然后再加上一个判断阈值就可以达到这一点。比如可以设置阈值为0.5,如果两个汉字的Word Embedding的语义相似性高于0.5,我们可以认为语义相同,否则认为语义不同。经过这个简单改造,理论上就整容出了一个语义版本的编辑距离了。
其实,通过这种改造,我们可以看出,如果把语义版编辑距离的阈值设定为1.0,也就是要求两个汉字的Word Embedding的Cosine相似性完全相同,这其实就退化成了标准的编辑距离了,也就是说,可以把标准编辑距离看做是语义编辑距离的一个特例情况。
当然,如果能够从单词语义匹配的角度来理解的话,可能会更好体会这种语义版的编辑距离的意义所在。我们可以继续改造,也很简单,就是先把两个句子先分词,分词后的每一个单词作为匹配单元,可以想象成一个单词对应edit和red例子中的一个英文字符,整个计算过程和上述的单字版的语义编辑距离是一样的。
比如还是这两个句子:
SentenceA:电脑多少钱
SentenceB:计算机价格
假设分词后的结果是:
SentenceA:电脑/多少钱
SentenceB:计算机/价格
那么基于单词的经典编辑距离为2:
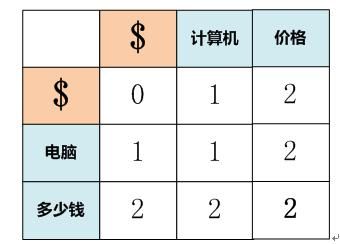
如果改造为语义版本,假设我们设定判断单词语义相同的阈值为0.5,同时假设通过单词Word Embedding计算的相似性如下:
Cosine(“计算机”,“电脑”)=0.7
Cosine(“计算机”,“多少钱”)=0.3
Cosine(“价格”,“电脑”)=0.4
Cosine(“价格”,“多少钱”)=0.8
那么其语义编辑距离为0,代表两者语义完全相同,其计算如下图所示:
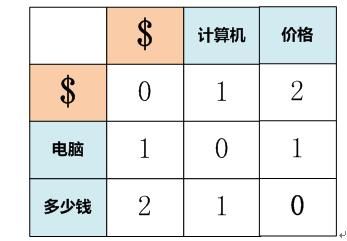
这样就能够通过编辑距离体现句子间的语义匹配程度了。如果语义编辑距离算出的值越大,说明两者语义距离越远,而如果两者之间的值越小,则说明两者语义距离越近。
|经典编辑距离vs 语义版编辑距离实验对比
因为编辑距离的分值不像Jaccard一样落在[0,1]之间,而是一个开放的整数值,而且这个整数值随着两个句子的情况不断变化,句子越长这个分值就可能越高,。为了便于比较,我们把两个句子的编辑距离得分划分成若干区间,比如[0,10],[10,20]….以10分作为一个区分段,然后高于100分值作为最后一个区间,这样就把编辑距离的分值划到了10个分数段内。
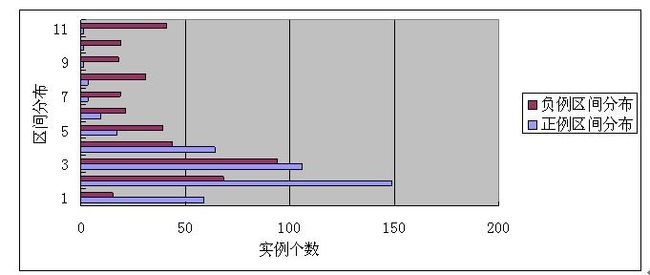
我们用下列方式来做经典编辑距离与语义版编辑距离的实验对比:做出一批语义相同的句子对作为正例,然后再做一批语义重叠但是又不同的句子对作为负例。然后对比两者的编辑距离分数在10个分数段内的分布情况,因为加上语义匹配后,会导致原先不匹配的片段现在匹配,所以无论是正例还是负例,其语义版本的编辑距离应该都会重心下移,就是分数减小,如果语义版编辑距离公式计算出正例的相似度得分整体偏低往下移的速度要大于负例下移的速度,那么说明语义版编辑距离在区分正例和负例过程中发生了作用。下面两图是两个模型的实验结果(纵轴1代表[0,10]分数段,2代表[11,20]分数段,以此类推)。
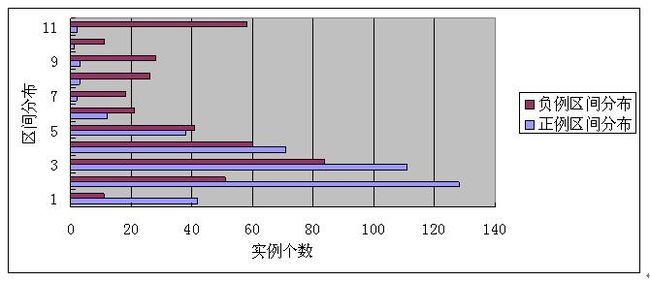
经典编辑距离正负例分值分布
语义编辑距离正负例分值分布(a=0.6)
从结果可以看出,语义版的编辑距离和经典编辑距离相比,无论是正例还是负例,分数段整个向下移动,就是算出的编辑距离都开始减小,这个是正常的,因为无论是正例还是负例,原先经典版本编辑距离不能匹配的语义部分由于现在可以匹配所以导致得分减小。值得注意的是,正例整体得分向下偏移的比例要大于负例向下偏移的比例,说明相同阈值下正例中语义匹配到的片段数目要远高于负例中语义匹配到的片段数目,这说明语义版编辑距离在区分正负例的过程中发挥了作用。
|穷人的语义处理工具箱中其它的可能工具
我们在“穷人的语义处理工具箱”两篇系列文章中介绍了使用Word Embeddding技术来对经典Jaccard、经典编辑距离进行语义版本的改造,并提出了语义版Jaccard以及语义版编辑距离,实验也证明了改进版本相对原始版本的优势。
上回书还提到了其实机器翻译评价指标BLEU、文本摘要评价指标ROUGH-N本质上也可以参照语义版Jaccard思路进行改造。发完后前阵子翻论文发现EMNLP2015有篇Short Paper就是这么去改的:Better Summarization Evaluation with Word Embeddings for ROUGE。BLEU也可以这么改,有兴趣的可以去试试。另外,ICML2015有篇论文:From Word Embeddings To Document Distances,其主体思路和本系列上回说的语义Jaccard主体思路也是类似的。这说明这种改造传统方法的思路虽然直观简单,看上去仿佛不够高大上,但是也算是一种创新模式。
其实还可以将这个系列继续进行下去,因为还有很多计算相似性的公式,都可以按照这个思路一一对其进行语义版本的改造,比如Pearson相关性、Tanimoto系数、马氏距离等等。
但是我们不准备继续这个话题了,因为通过两个实例已经将类似这种情形的通用改进思路讲清楚了,再这么改造下去连我自己都觉得无趣了,于是这个系列就到此为止打住吧,有兴趣的同学可以自己按照这种思路去改造新的语义版工具。
致谢:感谢畅捷通公司智能平台黄通文、桑海岩、薛会萍、沈磊等同事对于计算实现或训练语料收集方面的工作。
 扫一扫关注微信号:“布洛卡区” ,深度学习在自然语言处理等智能应用的技术研讨与科普公众号。
扫一扫关注微信号:“布洛卡区” ,深度学习在自然语言处理等智能应用的技术研讨与科普公众号。