红黑树面试必备,查询插入删除,多情景多图详细介绍
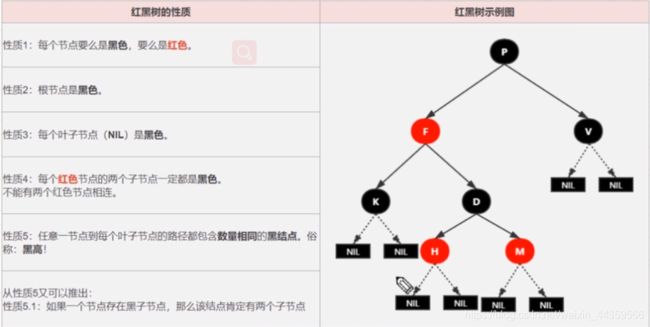
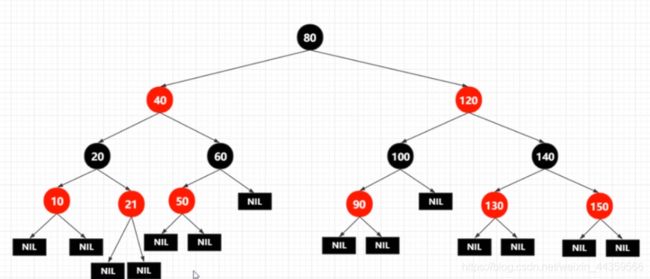
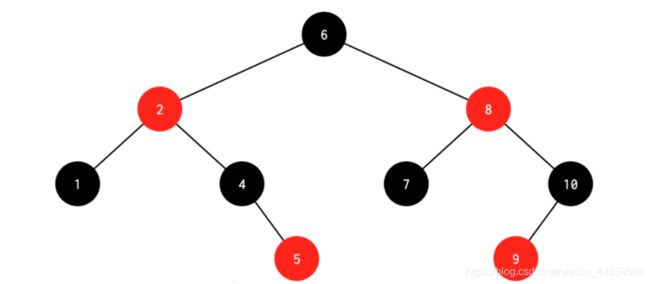
红黑树性质
解释性质
性质3的(NIL)也就是NULL,是叶子节点,黑色的。
性质5,如F节点,高度是3,包含NIL->K->F,NIL->H->D->F,NIL->M->D->F,每个路径的黑节点都只有2
性质6由以上解释的性质5可以推出
黑色完美平衡
红黑树并不是一个完美平衡二叉查找树, 从图上可以看到,根结点P的左子树显然比右子树高,但左子树和右子树的黑结点的层数是相等的,也即任意一个结点到每个叶子结点的路径都包含数量相同的黑结点(性质5)。所以我们叫红黑树这种平衡为黑色完美平衡。
红黑树的性质讲完了,只要这棵树满足以上性质,这棵树就是趋近与平衡状态的
左旋、右旋和变色
前面讲到红黑树能自平衡,它靠的是什么?三种操作:左旋、右旋和变色。
1.变色:结点的颜色由红变黑或由黑变红
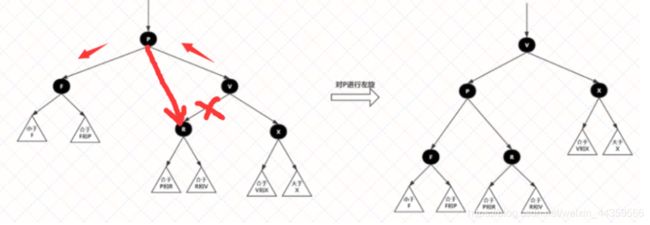
2.左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
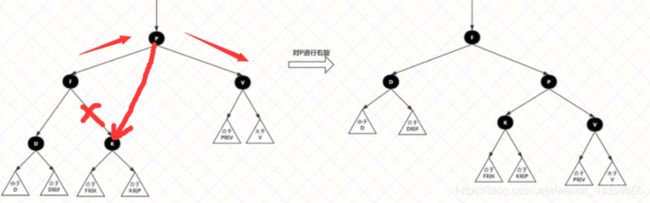
3.右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变
左旋图:
右旋图:
红黑树的插入
红插:插入的必须是红色(下面会讲)
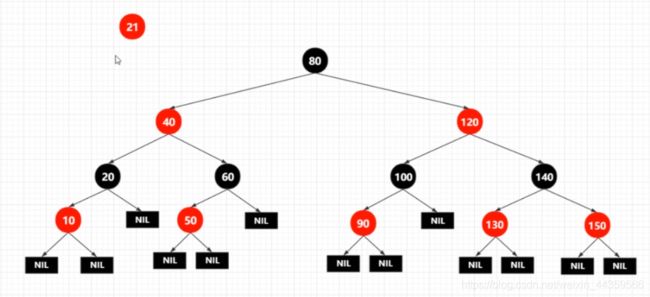
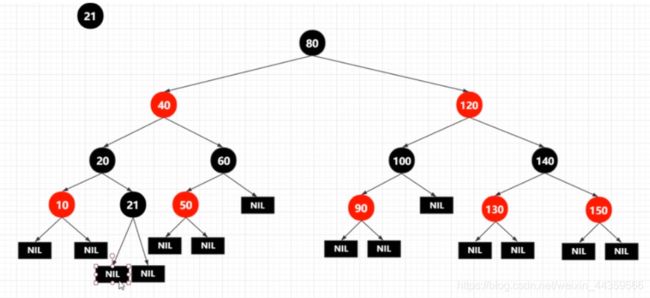
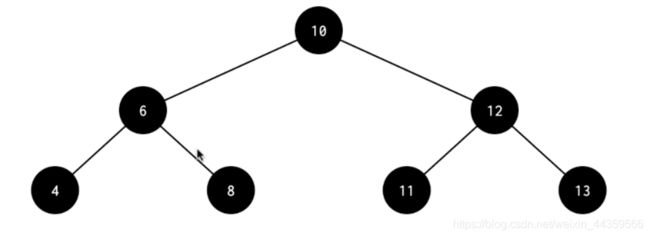
- 插入21,21比80小,插入80左子树,21比40小,插入40左子树,21比20大,插入20右子树,如下图所示。
如果插入是黑色的,会破坏性质5,即黑高
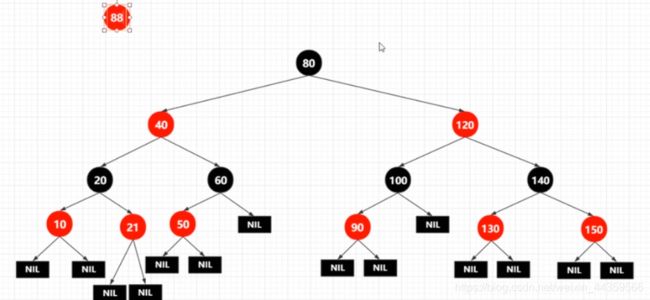
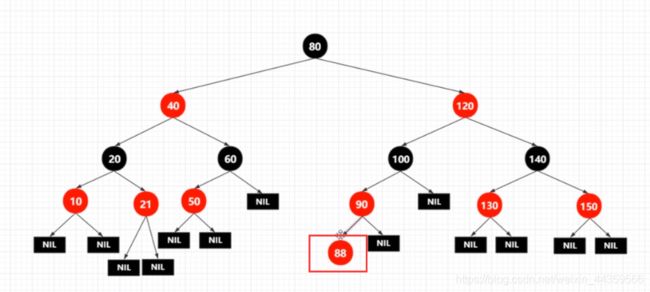
- 插入一个88
虽然是红插,但是破坏了性质4,即红节点90的两个子节点一定是黑色,不能有两个红节点相连,那咋办呢?(下面会讲)
插入操作包括两部分工作:
1.查找插入的位置
2.插入后自平衡
注意:插入节点,必须为红色,理由很简单,红色在父节点(如果存在)为黑色节点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。
但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
红黑树插入节点情景分析
情景1:红黑树为空树
最简单的一种情景,直接把插入结点作为根结点就行
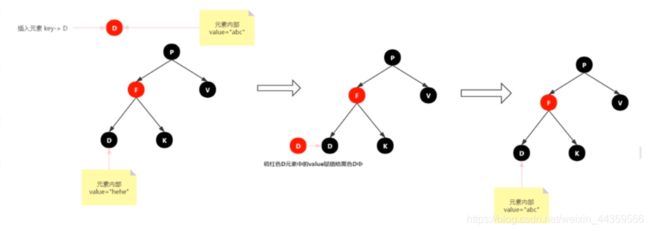
注意:根据红黑树性质2:根节点是黑色。还需要把插入结点设为黑色。
情景2:插入结点的Key已存在
处理:更新当前节点的值,为插入节点的值
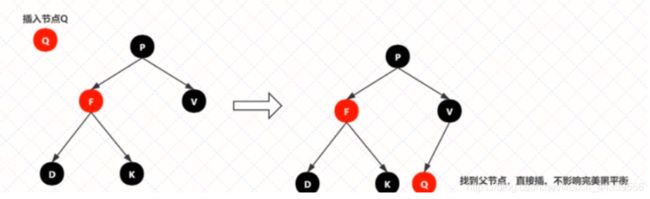
情景3:插入结点的父结点为黑结点
由于插入的结点是红色的,当插入结点的黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
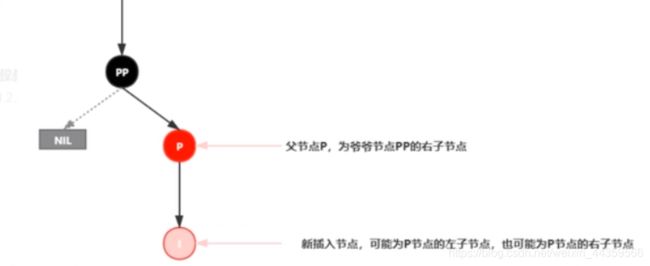
情景4:插入节点的父节点为红色
再次回想下红黑树的性质2:根结点是黑色。如果插入节点的父结点为红结点,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。
这一点很关键,因为后续的旋转操作肯定需要祖父结点的参与。
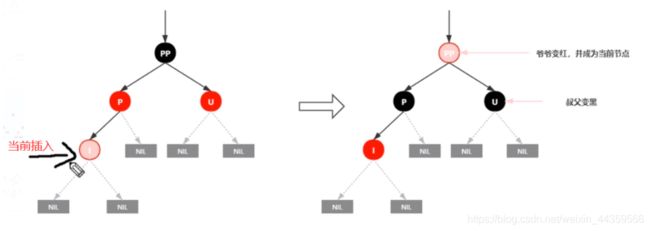
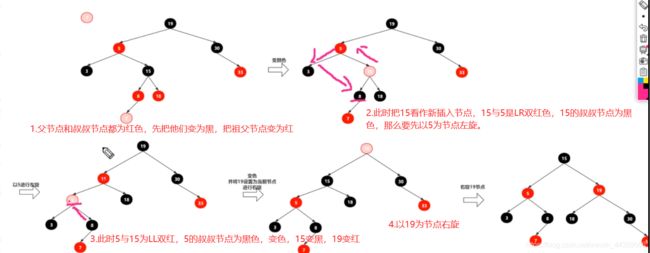
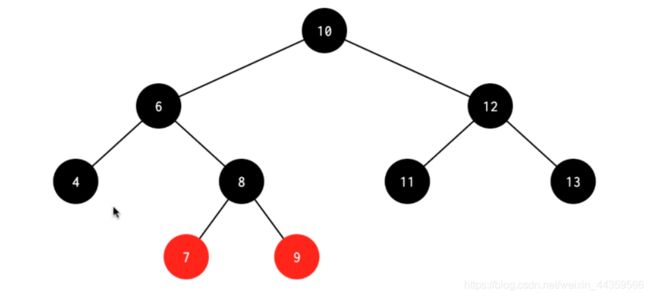
插入情景4.1:叔叔结点存在并且为红节点
依据红黑树性质4可知,红色节点不能相连=>祖父结点肯定为黑结点:
因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为:红黑红
处理:
1.将P和U节点改为黑色
2将PP改为红色
3.将PP设置为当前节点,进行后续处理
可以看到,我们把PP结点设为红色了,如果PP的父结点是黑色,那么无需再做任何处理;
但如果PP的父结点是红色,则违反红黑树性质了。所以需要将PP设置为当前节点,继续做插入操作自平衡处理,直到平衡为止,下面再介绍。
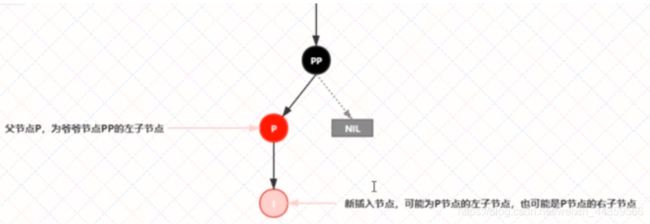
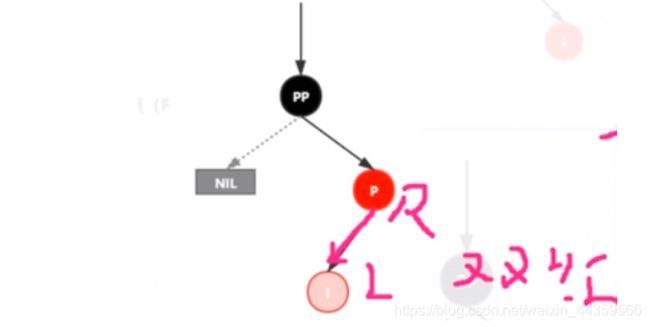
插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
注意:单纯从插入前来看,叔叔节点非红即空(NIL节点) ,否则的话破坏了红黑树性质5,此路径会比其它路径多-个黑色节点。
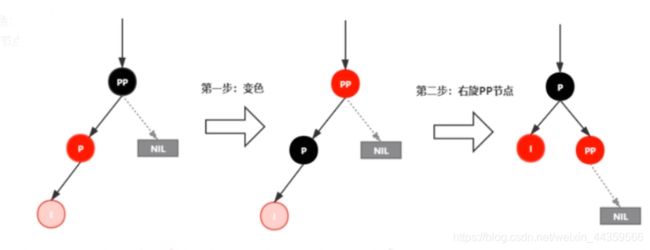
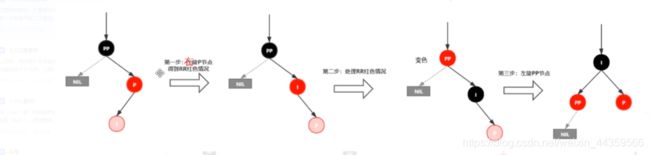
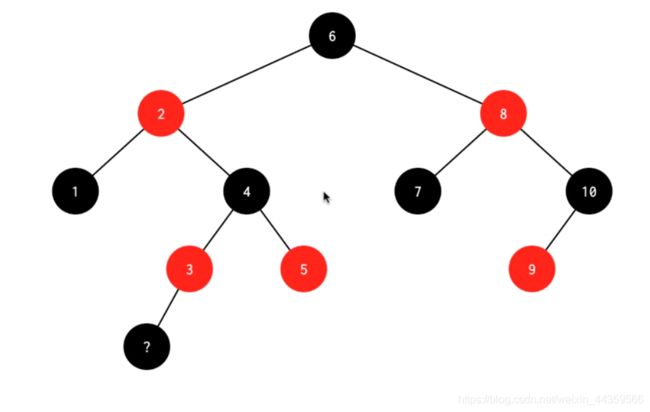
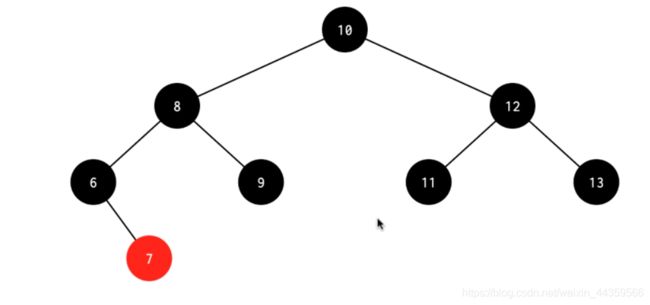
插入情景4.2.1:新插入节点,为其父节点的左子节点(LL双红色情况)
处理:
1.变颜色:将P设置为黑色,将PP设置为红色
2.对PP节点进行右旋
插入情景4.2.2:新插入节点,为其父节点的右子节点(LR红色情况)
处理:
插入情景4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
该情景对应情景4.2.只是方向反转,直接看图。
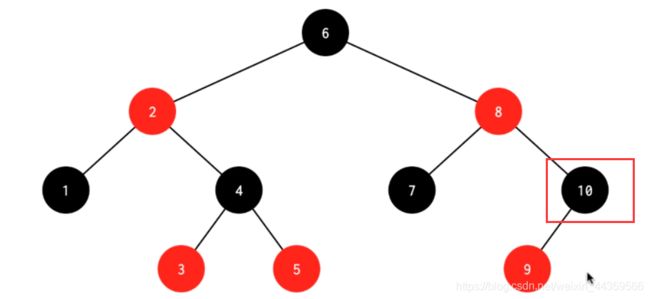
插入情景4.3.1:新插入节点,为其父节点的右子节点(RR红色情况)
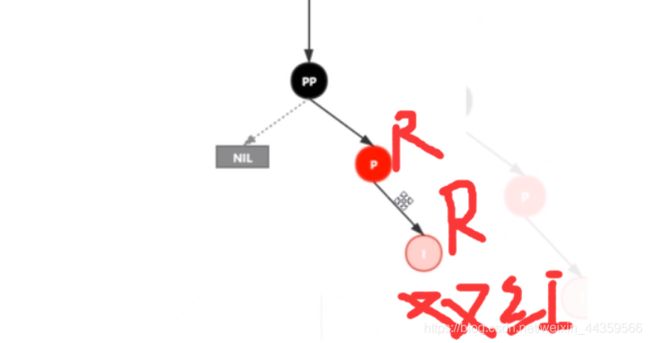
处理:
1.变颜色:将P设置为黑色,将PP设置为红色
2.对PP节点进行左旋
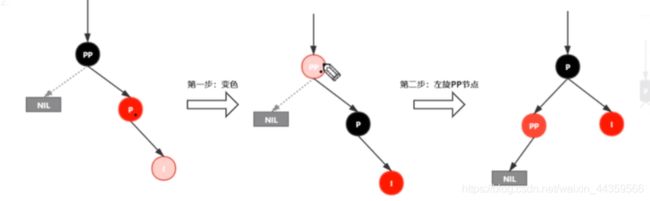
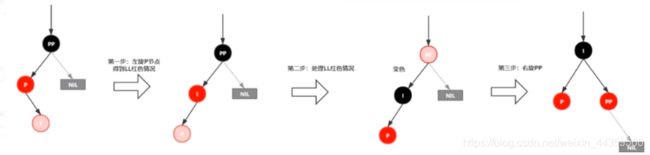
插入情景4.3.2:新插入节点,为其父节点的左子节点(RL红色情况)
处理:
1.对P进行右旋
2.将P设置为当前节点,得到RR红色情况
3.按照RR红色情况处理(1.变颜色2.左旋PP)
练习:
红黑树的删除
删除操作包括两部分工作:
1.查找删除的位置
2.删除后自平衡
查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;
当存在目标结点时,删除后就得做自平衡处理了。
删除了结点后我们还需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
二叉树删除结点找替代结点有3大种情情景:
- 情景1:若删除结点无子结点,如果是红色,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点)替换删除结点
删除操作的本质讲其实就是一个穷举的过程。
基于此,上面所说的3种二叉树的删除情景可以相互转换并且最终都是转换为情景1!
情景2:删除结点用其唯一的子结点替换,子结点替换为删除结点后,可以认为删除的是子结点,若子结点又有两个子结点,那么相当于转换为情景3,一直自顶向下转换,总是能转换为情景1。
情景3:删除结点用后继结点(肯定不存在左结点),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1。
第1种情景,删除红色节点(1种)
1.1红色结点无子结点,直接删除,例如删除结点3
可以达到平衡;
1.2红色节点有子结点,这样子是不平衡的,所以不存在。
第2种情景,删除黑色结点只有一个子结点(1种)
这个子结点只能是红色,因为根据性质5,要达到黑高,平衡,此时直接把黑色节点替换为其子结点,改为原来的黑色即可。
删除10
第3种情景:删除(或替换)黑色结点(无子结点)(7种)
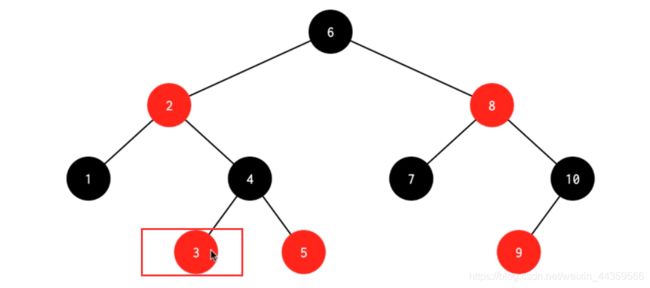
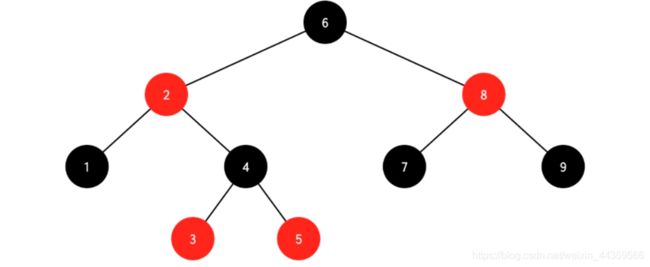
3.1 被删结点的父结点为红色结点,兄弟为黑色,兄弟的子结点为空(删除4)
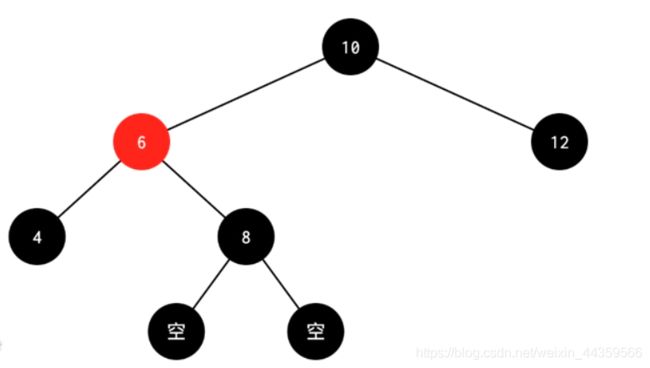
处理:删除4之后,左边黑色就少了1,为了平衡,所以要把删除结点的兄弟结点与父结点(红)换色,使得根节点左右两边的黑色高度一致。
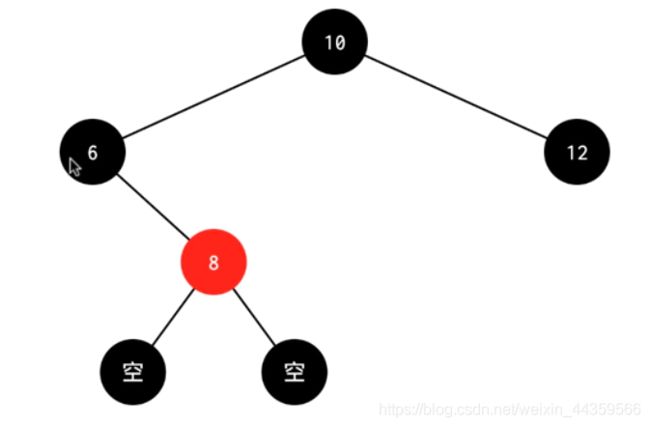
3.2 被删结点的父结点为红色结点,兄弟为黑色,兄弟的左子结点为红色(删除4)
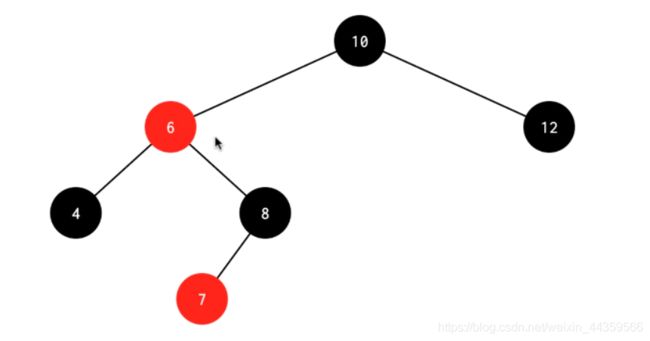
处理:先删除4,然后对兄弟结点进行右旋操作,得到下图1,这是双红,要交换7 8的颜色,然后对6结点进行左旋,得到下图2[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-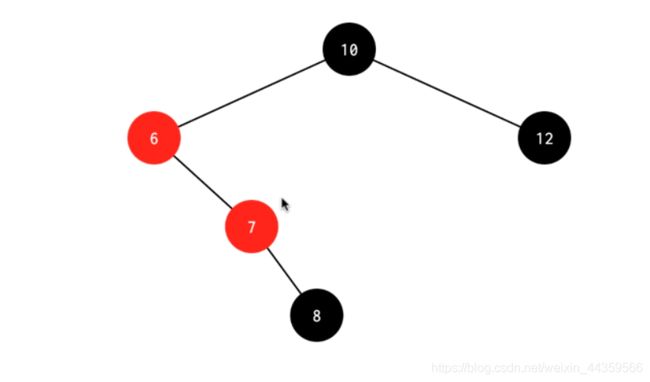
图1
3.3 被删结点的父结点为红色结点,兄弟为黑色,兄弟的右子结点为红色(删除4)
3.4被删结点的父结点为红色结点,兄弟为黑色,兄弟的左右子结点都为红色(删除4)
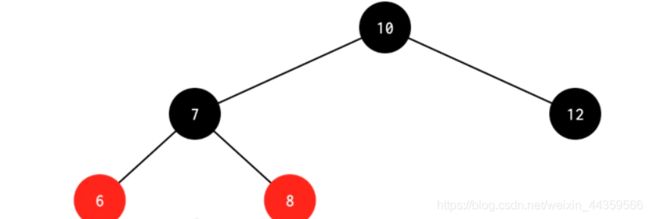
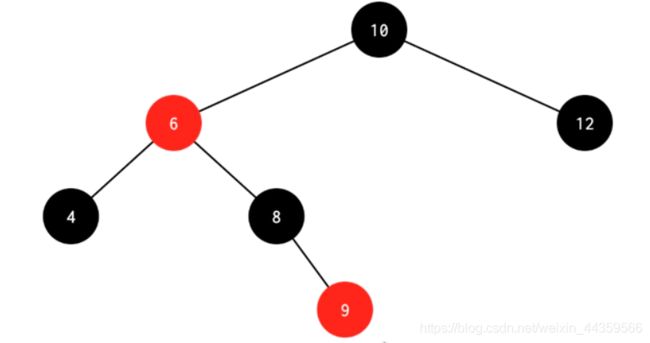
处理:先删除4,然后对其父节点进行左旋操作,得到如下图1,将8和两个子结点变色得到下图2
图1
图2
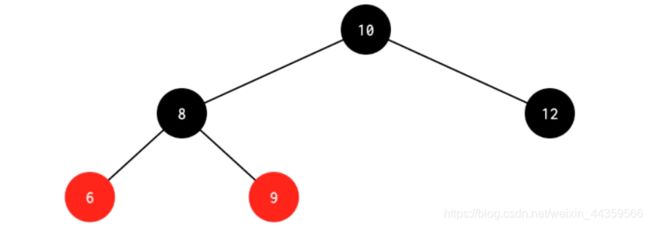
3.5 被删结点的父结点为黑色结点,兄弟为红色,兄弟的左右子结点都为黑色(删除4)
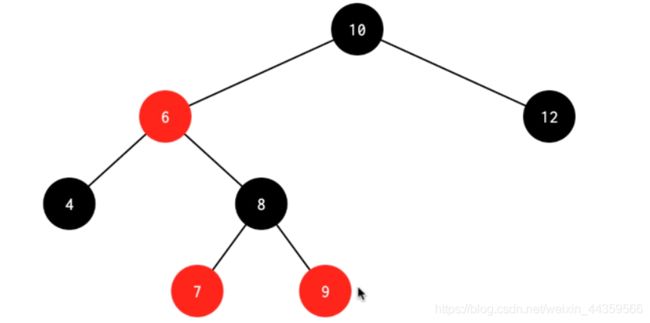
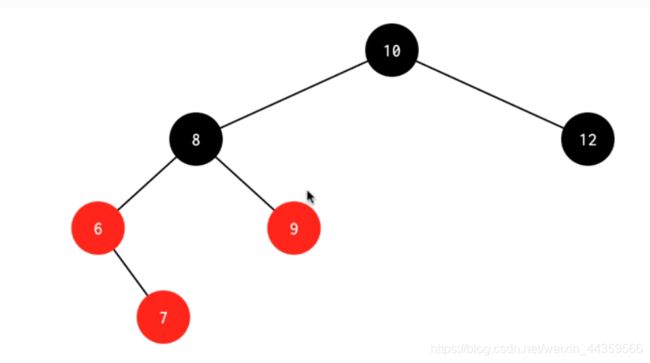
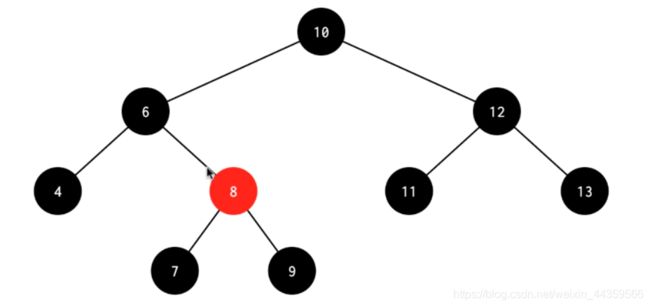
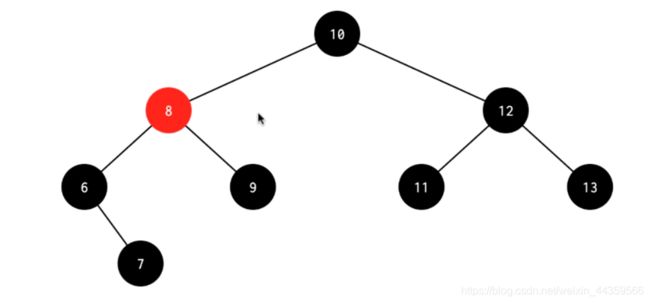
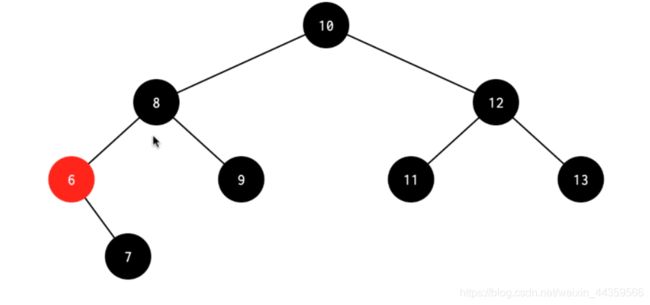
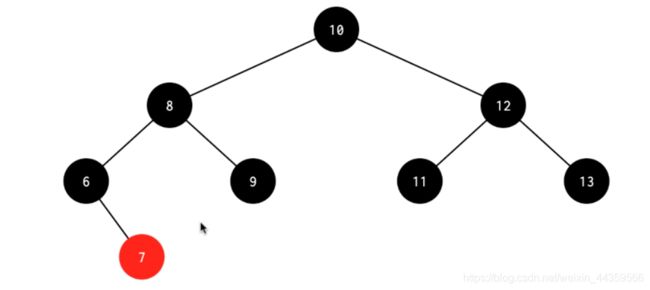
处理:先删除4,左旋其父节点6,得到下图1,将8和6换色,得到下图2,发现左边还差一个黑,交换6 7的颜色,得到最终结果图3
图1
图2
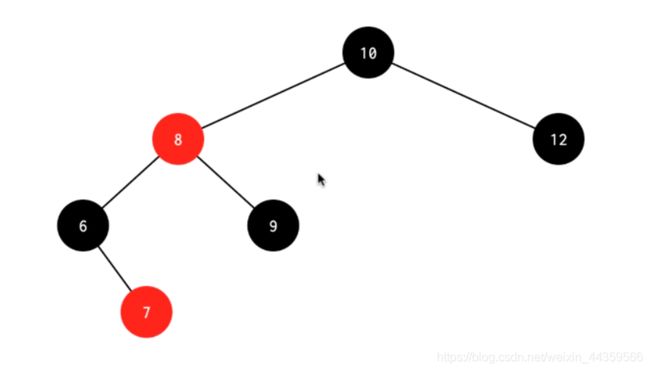
3.6被删结点的父结点为黑色结点,兄弟为黑色(删除4)
处理:先删除4,这是左边少了黑色,把8染红,此时10的左边只有2黑,右边有3黑,所以把6的兄弟染红,得到下图

3.7被删结点的父结点为黑色结点,兄弟为黑色,兄弟的左右子结点都为红色(删除4)
处理:先删除4,对其父节点6进行左旋,得到下图1,直接染黑9,得到最终结果图2
图1
图2