运动目标跟踪(九)--Struck跟踪原理
《Struck:Structured Output Tracking with Kernels》是 Sam Hare, Amir Saffari, Philip H. S. Torr等人于2011年发表在Computer Vision (ICCV)上的一篇文章。Struck与传统跟踪算法的不同之处在于:传统跟踪算法(下图右手边)将跟踪问题转化为一个分类问题,并通过在线学习技术更新目标模型。然而,为了达到更新的目的,通常需要将一些预估计的目标位置作为已知类别的训练样本,这些分类样本并不一定与实际目标一致,因此难以实现最佳的分类效果。而Struck算法(下图左手边)主要提出一种基于结构输出预测的自适应视觉目标跟踪的框架,通过明确引入输出空间满足跟踪功能,能够避免中间分类环节,直接输出跟踪结果。同时,为了保证实时性,该算法还引入了阈值机制,防止跟踪过程中支持向量的过增长。
最后,大牛作者们也提供了c++版源代码,有兴趣的朋友可以下载下来,体验下该算法的强大。代码下载地址:https://github.com/gnebehay/STRUCK,代码调试需要Opencv2.1以上版本以及Eigen v2.0.15。
在论文理解以及代码调试的过程中,主要参考了以下资料,感到获益匪浅,列举如下:
1) Eigen的安装及学习
http://eigen.tuxfamily.org/dox/GettingStarted.html
2) 支持向量机通俗导论(理解SVM的三重境界)
http://blog.csdn.net/v_july_v/article/details/7624837
实际上,作者提出的主要观点在于构建特征与类别的SVM,说穿了还是SVM的多标签回归,只是计算过程做了优化而已,利用SMO迭代出alpha,在此过程中,随机选取支持向量,不断优化正负类别样本,不断更新alpha,同时,始终把支持向量数目控制在一定阈值内。
另外一点,就是多类标签中,约束条件的计算优化。不断确保F(目标)》F(非目标)
目前在目标检测任务中,由于svm自身具有较好的推广能力以及对分类的鲁棒性,得到了越来越多的应用。 Struck算法便使用了在线结构输出svm学习方法去解决跟踪问题。不同于常规算法训练一个分类器,Struck算法直接通过预测函数: ,来预测每帧之间目标位置发生的变化,其中
,来预测每帧之间目标位置发生的变化,其中 表示搜寻空间,例如,
表示搜寻空间,例如, ,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为
,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为 (可见
(可见 其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
那么y预测函数 怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数
怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数![]()
![]()
 ,通过公式
,通过公式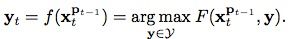 找到概率最大的
找到概率最大的 对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过
对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过 ,就可以成功找到目标啦~,至于搜寻空间
,就可以成功找到目标啦~,至于搜寻空间 如何取,在程序解读时大家就会看到了。
如何取,在程序解读时大家就会看到了。
那么如何找到 呢?我个人理解是:将判别函数形式转换为:
呢?我个人理解是:将判别函数形式转换为: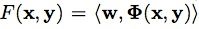 ,其中,
,其中, 表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数
表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数 来实现,该函数应满足条件:
来实现,该函数应满足条件: 和
和 ,其中,
,其中,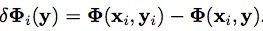 ,
, (
( 表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
接下来问题又来了,如何获得最小的w??文中采取的求解方式是利用拉格朗日对偶性,通过求解与原问题等价的对偶问题(dual problem),得到原始问题的最优解。通过给每一个约束条件加上一个拉格朗日乘子alpha,定义拉格朗日函数L(w,b,alpha)。一般对偶问题的求解过程如下:1)固定alpha,求L关于w,b的最小化。2)求L对alpha的极大。3)利用SMO算法求得拉格朗日乘子alpha。为了简化对偶问题求解,这里定义了参数beta,可见论文中的Eq.(8)。
算法主要流程:
1. 首先读入config.txt,初始化程序参数,这一过程主要由Config类实现;
2. 判断是否使用摄像头进行跟踪,如使用摄像头进行跟踪,则initBB=(120,80,80,80);
若使用视频序列进行跟踪,initBB由相应txt文件给出;
3. 将读入的每帧图像统一为320*240。
4. 由当前第一帧以及框initBB,实现对跟踪算法的初始化。
4.1 Initialise(frame,bb)
由于我们之前获取的initBB的坐标定义为float型,在这里首先将其转换为int型。
程序中选取haar特征,gaussian核函数, 初始化参数m_needsIntegralImage=true,m_needsIntegralHist=false。因此在这里,ImageRep image()主要实现了积分图的计算(如果特征为histogram,则可实现积分直方图的计算)。ImageRep类中的类成员包括frame,积分图,积分直方图。
4.2 UpdateLearner(image)
该函数主要实现对预测函数的更新,首先通过RadialSamples()获得5*16=80个样本,再加上原始目标,总共含有81个样本。之后判断这81个样本是否有超出图像边界的,超出的舍弃。将剩余的样本存入keptRects,其中,原始目标样本存入keptRects[0]。定义一个多样本类MultiSample,该类中的类成员主要包括样本框以及ImageRep image。并通过Update(sample,0)来实现预测函数的更新。
4.3 Update(sample,0)
该函数定义在LaRank类下,文章中参考文献《Solving multiclass support vector machines with LaRank》提到了这种算法。当我们分析LaRank头文件时,可看到struck算法重要步骤全部聚集在这个类中。该类中的类成员包括支持模式SupportPattern,支持向量SupportVector,Config类对象m_config,Features类对象m_features,Kernel类对象m_kernel,存放SupportPattern的m_sps,存放SupportVector的m_svs,用于显示的m_debugImage,目标函数中的系数m_C,矩阵m_K。
查看
SupportPattern的定义,我们知道该结构主要包括x(存放特征值),yv( ,存放目标变化关系),images(存放图片样本),y(索引值,表明指定样本存放位置),refCount(统计sv的个数??)。
同样,查看SupportVector的定义可知,该结构包括一个
SupportPattern,y(索引值,表明指定样本存放位置),b(beta),g(gradient),image(存放图片样本)。
,存放目标变化关系),images(存放图片样本),y(索引值,表明指定样本存放位置),refCount(统计sv的个数??)。
同样,查看SupportVector的定义可知,该结构包括一个
SupportPattern,y(索引值,表明指定样本存放位置),b(beta),g(gradient),image(存放图片样本)。
在函数Update(sample,0)中,定义了一个SupportPattern* sp。首先对于每个样本框,其x,y坐标分别减去原始目标框的x,y坐标,将结果存入sp->yv。然后对于每个样本框内的图片统一尺寸为30*30,并存入sp->images。对于每个样本框,计算其haar特征值,并存入sp->x。令sp->y=y=0,sp->refCount=0,最后将当前sp存入m_sps。
4.3.1 ProcessNew(int ind)
之后执行ProcessNew(int ind),其中ind=m_sps.size()-1。由于每处理一帧图像,m_sps的数量都增加1,这样定义ind能够保证ProcessNew所处理的样本都是最新的样本。
在
ProcessNew处理之前,
首先看函数AddSupportVector(SupportPattern* x,int y,double g)的定义:
SupportVector* sv=new SupportVector;定义了一个支持向量。
为支持向量赋初值:sv->b=0.0,sv->x=x,sv->y=y,sv->g=g,并将该向量存入m_svs。接下来通过调用Kernel类中的Eval()函数更新核矩阵,即m_K,以后用于Algorithm 1
计算。
现在再回到ProcessNew函数:
第一个AddSupportVector(),
将目标框作为参数,增加一个支持向量
存入m_svs,此时,m_svs.size()=1,m_K(0,0)=1.0,函数返回ip=0。
之后执行MinGradiernt(int ind),求得公式10中的g最小值。返回最小梯度的数值以及对应的样本框存放位置。
第二个
AddSupportVector(),将具有最小梯度的样本框作为参数,增加一个特征向量存入m_svs,此时,m_svs.size()=2,并求得m_K(0,1),m_K(1,0),m_K(1,1)。函数返回in=1。
之后进行SMO算法进行计算,若某向量的beta值为0,则舍弃该支持向量。
4.3.2 BudgetMaintenance()
再之后执行函数BudgetMaintenance(),保证支持向量个数没有超过100。
4.3.3 Reprocess()
进行Reprocess()步骤,一个Reprocess()包括1个ProcessOld()和10个Optimize();
ProcessOld()主要对已经存在的SupportPattern进行随机选取并处理。和ProcessNew不同的地方是,这里将满足梯度最大以及满足 的支持向量作为正支持向量。负支持向量依然根据梯度最小进行选取。之后再次执行SMO算法,判断这些支持向量是否有效。
的支持向量作为正支持向量。负支持向量依然根据梯度最小进行选取。之后再次执行SMO算法,判断这些支持向量是否有效。
Optimize()也是对已经存在的SupportPattern进行随机选取并处理,但仅仅是对现有的支持向量的beta值进行调整,并不加入新的支持向量。正负支持向量的选取方式和ProcessOld()一样。
4.3.4 BudgetMaintenance()
执行函数BudgetMaintenance(),保证支持向量个数没有超过100。
5.跟踪模块(Algorithm 2)
首先通过ImageRep image()实现积分图的计算,然后进行抽样(这里抽样的结果和初始化时的抽样结果不一样,大概抽取几千个样本)。将超出图像范围的框舍弃,剩余的保留在keptRects中。对keptRects中的每一个框,计算F函数,即 ,将结果保存在scores里,并记录值最大的那一个,将其作为跟踪结果。
UpdateDebugImage()函数主要实现程序运行时显示的界面。
UpdateLearner(image)同步骤4一致。
,将结果保存在scores里,并记录值最大的那一个,将其作为跟踪结果。
UpdateDebugImage()函数主要实现程序运行时显示的界面。
UpdateLearner(image)同步骤4一致。
