红黑树的特性和实现
平衡二叉搜索树的形式多样,且各具特色。比如,伸展树实现简便、无需修改节点 结构、分摊复杂度低,但可惜最坏情况下的单次操作需要n时间,故难以适用于对可靠性和稳定性要求极高的场合。
反之,AVL树尽管可以保证最坏情况下的单次操作速度,但需在节点中嵌入平衡因子等标识;更重要的是,删除操作之后的重平衡可能需做多达logn次旋转,从而频繁地导致全树整体拓扑结构的大幅度变化。
红黑树即是针对后一不足的改进。通过为节点指定颜色,并巧妙地动态调整,红黑树可保证: 在每次插入或删除操作之后的重平衡过程中,全树拓扑结构的更新仅涉及常数个节点。尽管最坏情况下需对多达logn个节点重染色,但就分摊意义而言仅为O(1)个
当然,为此首先需在AVL树“适度平衡”标准的基础上,进一步放宽条件。实际上,红黑树所采用的“适度平衡”标准,可大致表述为:任一节点左、右子树的高度,相差不得超过两倍。
定义与条件
为便于对红黑树的理解、实现与分析,这里不妨下图所示统一地引入n + 1个外部节点,以保证原树中每一节点(现称作内部节点,白色八角形)的左、右孩子均非空—尽管有可能其中之一甚至二者同时是外部节点。

这些外部节点的引入只是假想式的,在具体实现时并 不一定需要兑现为真实的节点。如此扩展之后的便利 之处在于,我们的考查范围只需覆盖真二叉树。
由红、黑两色节点组成的二叉搜索树若满足以下条件,即为红黑树(red-black tree):
- (1) 树根始终为黑色
- (2) 外部节点均为黑色
- (3) 其余节点若为红色,则其孩子节点必为黑色
- (4) 从任一外部节点到根节点的沿途,黑节点的数目相等
条件(1)和(2)意味着红节点均为内部节点,且其父节点及左、右孩子必然存在。
条件(3)意味着红节点之父必为黑色,因此树中任一通路都不含相邻的红节点。
由此可知,在从根节点通往任一节点的沿途,黑节点都不少于红节点。除去根节点本身,沿 途所经黑节点的总数称作该节点的黑深度(black depth)–根节点的黑深度为0,其余依此类推。故条件(4)亦可等效地理解和描述为“所有外部节点的黑深度统一”。
由条件(4)可进一步推知,在从任一节点通往其任一后代外部节点的沿途,黑节点的总数亦 必相等。除去(黑色)外部节点,沿途所经黑节点的总数称作该节点的黑高度(black height)。 如此,所有外部节点的黑高度均为0,其余依此类推。
特别地,根节点的黑高度亦称作全树的黑高度,在数值上与外部节点的黑深度相等。
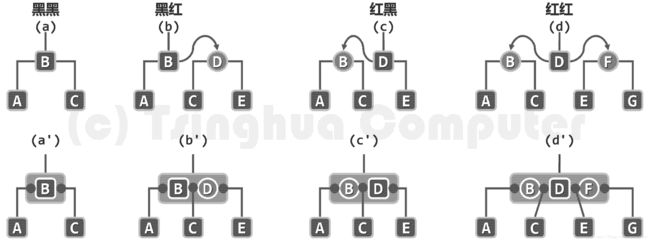
在红黑树与4阶B-树之间,存在极其密切的联系; 经适当转换之后,二者相互等价!
具体地,自顶而下逐层考查红黑树各节点。每遇到一个红节点,都将对应的子树整体提升一 层,从而与其父节点(必黑)水平对齐,二者之间的联边则相应地调整为横向。
照此理解,此时的关键码也被赋予了对应的颜色。对照红黑 树的条件,(2,4)B-树中的每个节点应包含且仅包含一个黑关键码,同时红关键码不得超过两个。 而且,若某个节点果真包含两个红关键码,则黑关键码的位置必然居中。
与前文介绍二叉平衡树的其他成员的时候一样,接下来将学习在插上,删除的等操作的时候如何保障其红黑树的特性。
红黑树的节点新增
红黑数的新增过程,经调用查找之后,确认目标节点尚不存在。于是,在查找终止的位置x处创建节点,并随即将其染成红色(除非此时全树仅含一个节点)。
现在,对照红黑树的上述四项条件,唯有(3)未必满足,此时x的父亲也可能是红色。
因新节点的引入,而导致父子节点同为红色的此类情况,称作“双红”(double red)。 此时,当前节点x的兄弟及两个孩子(初始时都是外部节点),始终均为黑色。
将x的父亲与祖父分别记作p和g。既然此前的红黑树合法,故作为红节点p的父亲,g必然存 在且为黑色。g作为内部节点,其另一孩子(即p的兄弟、x的叔父)也必然存在,将其记作u。 以下,视节点u的颜色不同,分两类情况分别处置。
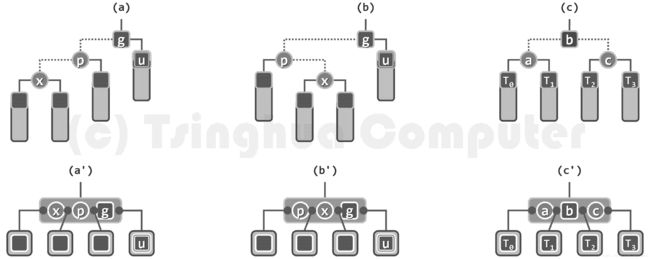
此时红黑树条件(3)的违反,从B-树角度等效地看,即同一节点不应包含紧邻的红色关键码。
故按如上图(c’)所示,只需令黑色关键码与紧邻的红色关键码互换颜色。从图(c)红黑树的角度看,这等效于按中序遍历次序,对节点x、p和g及其四棵子树,做一次局部“3 + 4”重构(对于“3 + 4”重构,详见:https://blog.csdn.net/canot/article/details/78946450)。
由于该3+4重构过程中,根节点b最终肯定为黑色,不会导致向上传播的现象。
双红修正-u为红色
节点u为红色的情况。此时,u的左、右孩子非空且均为黑色,其黑高度必与x的兄弟
以及两个孩子相等。
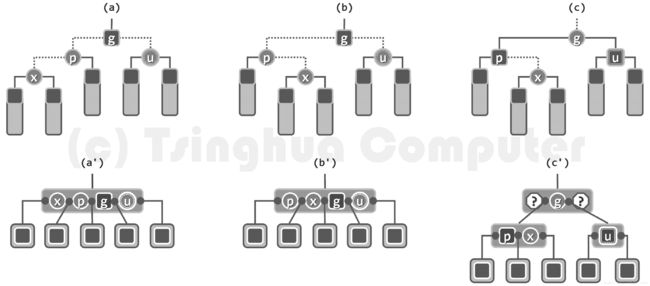
如上图的a,b两种情况。此时红黑树条件(3)的违反,从B-树角度等效地看,即该节点因超过4度而发生上溢。
从图(c)红黑树的角度来看,只需将红节点p和u转为黑色,黑节点g转为红色,x保持红色。从图(c’)B-树的角度来看,等效于上溢节点的一次分裂。
如此调整之后局部子树的黑高度复原。然而,子树根节点g转为红色之后,有可 能在更高层再次引发双红现象。 即B-树中的上溢的传播,此时可以等效地将g视作新插入的节点,同样地分以上两类情况如法处置。请注意, 每经过一次这样的迭代,节点g都将在B-树中(作为关键码)上升一层,而在红黑树中存在双红缺陷的位置也将相应地上升两层,故累计至多迭代O(logn)次。若最后一步迭代之后导致原树根的分裂,并由g独立地构成新的树根节点,则应遵 照红黑树条件(1)的要求,强行将其转为黑色。此时,全树的黑高度随即增加一层。
红黑树节点删除
假设删除节点为x。在删除x的过程中,如果x不是叶子节点,在将x与其中序遍历中的后继节点交换。此时x则一定为叶子节点,并且一定无左孩子,假设其删除后的接替节点即右孩子为r。并设p = _hot为x的父亲。
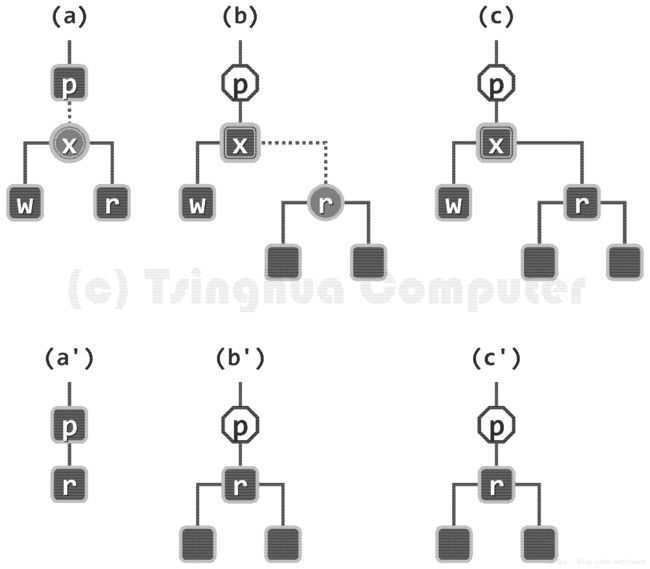
如上图所示,除了其接替者r, x还应有另一个孩子—左孩子w,且w必为(黑色的)外部节点 NULL。
如图(a)和(a’)所示,若x为红色,则在删除x并代之以r后,条件 (3~4)依然满足;
反之,若x为黑色, 则要看其替代者r的颜色,如图(b)和(b’)所示,若r为红色,则只需将其翻转为黑色,即可使条件(3~4)重新满足。
然而如图(c)和(c’)所示,若x和r均为黑色,则为使条件(3~4)重新成 立,还需要做略微复杂一些的处理。
因某一无红色孩子的黑节点被删除,而导致的此类复杂情况,称作“双黑”(double black) 现象。
原黑节点x的兄弟必然非空(保证节点到所有外部节点到黑节点数量一致),将其记作s;
x的父亲记作p,其颜色不确定(八角形示意)。以下视s和p颜色的不同组合,按四种情况分别处置。
双黑修正—1
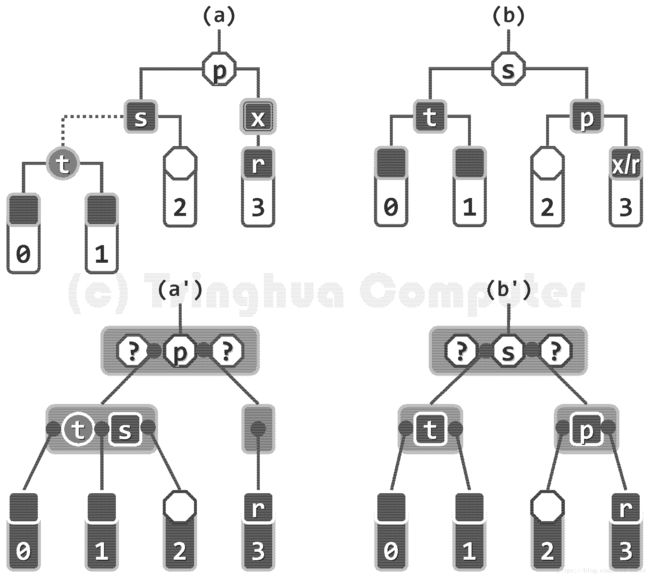
既然节点x的另一孩子w = NULL,故从B-树角度看节点x被删除之后的情况(上图a’),
可以等效地理解为: 关键码x原所属的节点发生下溢;此时,t和s必然属于B-树的同一节点,且该节点就是下溢节点的兄弟。故可参照B-树的调整方法,下溢节点从父节点借出一个关键码(p), 然后父节点从向下溢节点的兄弟节点借出一个关键码(s),调整后的效果如图(b’)。
从红黑树的角度(图(b))来看, 上述调整过程等效于,对节点t、s和p 实施“3 + 4”重构。
此外,根据红黑树与B-树的对应关系不难理解,若这三个节点按中序遍历次序重命名为a、b和c,则还需将a 和c染成黑色,b则继承p此前的颜色。 就上图具体实例而言,也就是将t和p染成黑色,s继承p此前的颜色。注意,整个过程中节点r保持黑色不变。
双黑修正—2
节点s及其两个孩子均为黑色时,视节点p颜色的不同,又可进一步分为两种情况。
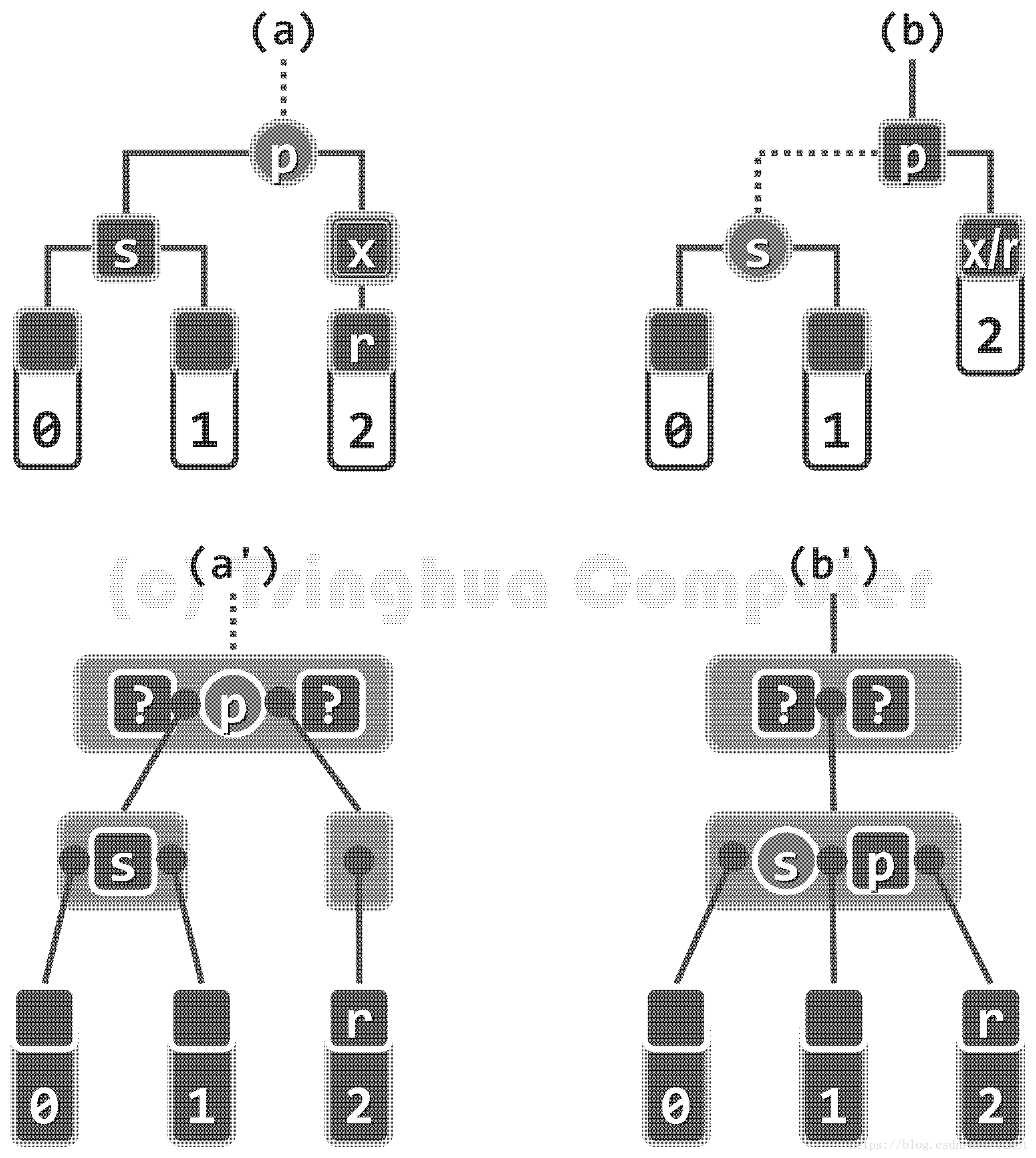
先考虑p为红色的情况。如上图所示。
在对应的B-树中,关键码x的删除导致其所属的节点下溢。但因此时关键码s所在节点只有两 个分支,故下溢节点无法从父节点借出关键码(p)。
按照前文的B-树平衡算法,此时应如图(b’)所 示,将关键码p取出并下降一层,然后以之为“粘合剂”, 将原左、右孩子合并为一个节点。从红黑树角度看,这 一过程可如图(b)所示等效地理解为: s和p颜色互换。
由图(b)(及其对称情况)可知,经过以上处理,红黑树的所有条件都在此局部得以恢复。另外,由于关键码p原为红色,故如图8.30(a’)所示,在关键码p所属节点中,其左或右必然还有一个黑色关键码(当然, 不可能左、右兼有)–这意味着,在关键码p从其中取 出之后,不致引发新的下溢。至此,红黑树条件亦必在 全局得以恢复,删除操作即告完成。
双黑修正–3
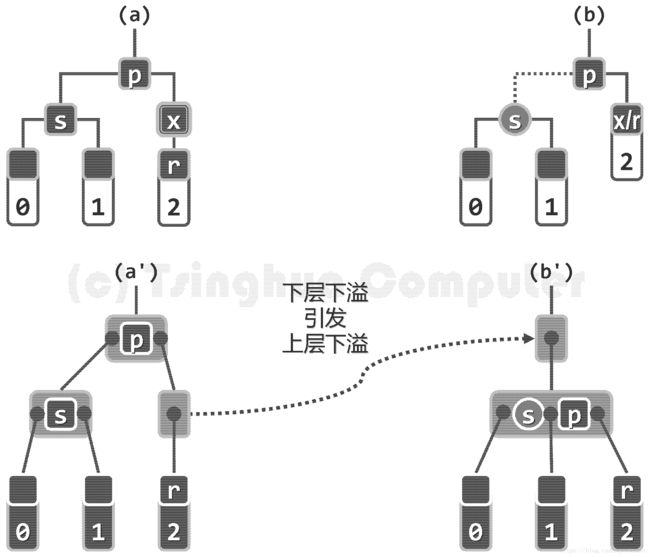
接下来,再考虑节点s、s的两个孩子以及节点p均为黑色的情况。 如图(a)所示,在对应的B-树中,因关键码x的删除,导致其所属节点发生下溢。
因此可如图(b’)所示,将下溢节点与其兄弟合并。从红黑树的角度来看,这一过程可如图(b)所示等效地理解为: 节点s由黑转红。
由图(b)可知,经以上处理,红黑树所有条件都在此局部得到恢复。
然而,因s和x在此之前均为黑色,故如图(a’)所示,p原所属的B-树节点必然仅含p这一个关 键码。于是在p被借出之后,该节点 必将继而发生下溢,故有待于后续进一步修正。
从红黑树的角度来看,此时的状态可等效地理解为: 节点p的父节点刚被删除。当然,可以 按照本节所介绍的算法,视具体的情况继续调整。
实际上稍后总结时将会看出,这也是双黑修正过程中,需要再次迭代的唯一可能。幸运的是, 尽管此类情况可能持续发生,下溢的位置也必然不断上升,故至多迭代O(logn)次后必然终止。
双黑修正-4
最后,考虑节点s为红色的情况。
如图a所示作为红节点s的父亲,节点p必为黑色;
同时,s的两个孩子也应均为黑色。
于是从B-树的角度来看,只需如图(b’)所示,令关键码s与p互换 颜色,即可得到一棵与之完全等价的B-树。而从红黑树的角度来看, 这一转换对应于以节点p为轴做一次旋转,并交换节点s与p的颜色。
经过这一转换之后,情况已经发生了微妙而本质的变化。仔细观察图(b)不难发现, 在转换之后的红黑树中,被删除节点x(及其替代者节点r)有了一个新的兄弟s’–与此前的 兄弟s不同,s’必然是黑的!这就意味着,接下来可以套用此前所介绍其它情况(1和2)的处置方法,继续并最终完成双黑修正。