Python算法总结（六）决策树回归（附手写python实现代码）

注：可结合”Python算法总结（三）决策树分类（附手写python实现代码）“一起阅读！

一、算法类型

有监督的回归算法

二、手写python算法

基于CART算法的python实现。
CART算法特点：①每个特征的重要程度是不一样，②每个连续型特征的不同分箱的重要程度是不一样的。

# 辅助函数1：切分数据集函数
def binsplitdataset(dataset,feature_index,value):
    '''
    参数说明：
        dataset是带有标签的数据集
        feature_name用于切分的特征
        value该切分特征的切分点
    返回：按featurename特征的value切分的数据集2个    
    '''
    dataset_0=dataset[dataset.iloc[:,feature_index] >  value]
    dataset_1=dataset[dataset.iloc[:,feature_index] <= value]
    return dataset_0,dataset_1

# 辅助函数2：计算切分误差函数
def error(dataset):
    '''
    参数说明：dataset是带有标签的数据集
    返回：数据集标签列的误差值，误差值=方差*样本数量，
        为何乘以样本数量？回答：“子样本数量=切分子集样本占总样本的比重*总样本数量”，即每个子样本的误差同比放大“总样本数量”倍数。
        便于后续横向比较不同切分的误差值。
    '''
    err=dataset.iloc[:,-1].var() * dataset.shape[0]
    return err

# 辅助函数3：生成叶节点的函数
def leaf_label(dataset):
    '''
    参数说明：dataset是叶子节点的带有标签的数据集
    返回：叶子节点的标签取值，用指标平均值
    '''
    m_label=dataset.iloc[:,-1].mean()
    return m_label

# 主函数1：寻找最佳切分特征函数
def bestsplit(dataset,leaf_label=leaf_label,error=error,min_error=1,min_samples_leaf=5,min_samples_split=10):
    '''
    参数说明：dataset是叶子节点的带有标签的数据集
    返回：
        或：
        best_feature_index：最佳切分特征的索引
        best_feature_value：最佳切分特征的最佳切分点
        或：
        None:空值
        leaf_label(dataset)：叶子节点的标签取值
        
    ''' 
    # 如果数据集标签值是重复值，只有一个取值，则不分支
    if len(set(dataset.iloc[:,-1].values))==1:
        return None,leaf_label(dataset)
    
    # 如果数据集标签值大于1，则考虑分支
    N,M=dataset.shape
    
    E=error(dataset) #父节点的总误差
    best_error=np.inf #最佳误差，初始化，float格式
    best_feature_index=0
    best_feature_value=0
    
    #进一步，如果数据集样本量少于阈值，则不分支
    if N < min_samples_split:  #分支前判断
        return None,leaf_label(dataset)
    
    #如果数据样本量多于阈值，则考虑分支
    #遍历所有特征
    for m in range(M-1):
        m_all_values=set(dataset.iloc[:,m].values)
        #遍历所有特征值
        for m_value in m_all_values:
            dataset_0,dataset_1=binsplitdataset(dataset,m,m_value)
            
            #如分支后的子样本集的样本量小于阈值，则退出本次小循环
            if dataset_0.shape[0]<min_samples_leaf or dataset_1.shape[0]<min_samples_leaf:
                continue  #如果都没有符合条件的情况，要返回什么？
            
            err_m=error(dataset_0)+error(dataset_1) #分支后子节点的误差总和
            if err_m < best_error:
                best_error=err_m
                best_feature_index=m
                best_feature_value=m_value
    
    #再进一步，如果“误差增益“小于阈值，说明分支效果不明显，则不分支
    error_gain=E-best_error
    if error_gain<min_error:
        return None,leaf_label(dataset)
    
    #对上面”continue“的补充，否则return将有误。
    dataset_0,dataset_1=binsplitdataset(dataset,best_feature_index,best_feature_value)
    if dataset_0.shape[0]<min_samples_leaf or dataset_1.shape[0]<min_samples_leaf:
        return None,leaf_label(dataset)
    
    return best_feature_index,best_feature_value

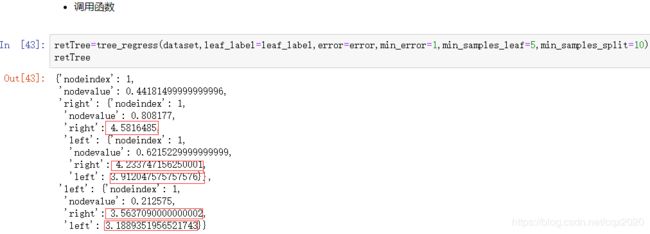
# 主函数2：构建决策回归数函数
def tree_regress(dataset,leaf_label=leaf_label,error=error,min_error=1,min_samples_leaf=5,min_samples_split=10):
    '''
    返回：
    retTree:回归树，字典格式
    '''
    feature_index,feature_value=bestsplit(dataset,leaf_label=leaf_label,error=error,min_error=1,min_samples_leaf=5,min_samples_split=10)
    
    if feature_index==None:
        return feature_value #其实是叶子节点的标签取值
    
    #回归树保存在字典中，key是特征索引，value是特征取值
    retTree={}
    retTree['nodeindex']=feature_index
    retTree['nodevalue']=feature_value
    
    dataset_0,dataset_1=binsplitdataset(dataset,feature_index,feature_value)
    retTree['right']=tree_regress(dataset_0,leaf_label=leaf_label,error=error,min_error=1,min_samples_leaf=5,min_samples_split=10)
    retTree['left']=tree_regress(dataset_1,leaf_label=leaf_label,error=error,min_error=1,min_samples_leaf=5,min_samples_split=10)
    
    return retTree

三、附调用手写函数

参考：http://edu.cda.cn/course/966