二叉树介绍与详解(一)
二叉树是一个高级数据结构,它的特点是既可以像索引一样快速查找,又可以像链表一样快速插入。是一个智慧结晶啊,那么接下来就要全面介绍一下二叉树。
一、二叉树含义
二叉树是一种简单的树结构,每一个父节点下最多只能有两个子节点。
二叉树是一种常用的数据结构,是Java语言中非常重要的数据结构,他比数组和链表更加的快速实用,也是很多高级结构的底层结构,如:堆内存结构。
二、为什么要学习二叉树?
在树中查找数据项的速度和在有序数组中查找一样快,并且插入数据像和删除数据项的速度和在链表中一样快。
二叉树结合了数组与链表结构的优点,成为了更加快速的高级数据结构。
三、什么是二叉树?
在计算机科学中,二叉树是每个结点最多有两个子树的树结构,通常子树被称为”左子树”(left subtree) 和 ”右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
四、树的术语
4.1 路径
从一个节点走到另一个节点,所经过的节点的顺序排列称为路径。(路径有且只有一条)
4.2 根
树顶端的节点称为根,一棵树只有一个根节点。从一个节点到另外一个节点只有一个路径。
4.3 父节点
除根节点以外,每个节点都有一个向上连接到的节点,上面的这个节点称为父节点。
4.4 子节点
每个节点都可能有一条或者多条边向下连接其他节点,下面的这些节点称为子节点。
4.5 叶节点
没有子节点的节点称为叶节点。
4.6 子树
每个节点都可以作为子树的根,一个节点的子树包含它所有的子孙。
4.7 访问
当程序控制流程达到某个节点时,就称为访问这个节点。
4.8 遍历
遍历树意味着要遵循某种特定的顺序访问树中的所有节点。
4.9 层
一个节点的层数据是指从根开始到这个节点有多少代。
4.10 关键字
用户查询数据位置的关键字值。
4.11 二叉树
如果树中每个节点最多只能有两个子节点,这样的树称为二叉树。
4.12 树
树是一个类型的统称,二叉树为树的一种。
五、树的五种基本形态
- 二叉树可以是空集
2. 根可以有空的左右子树
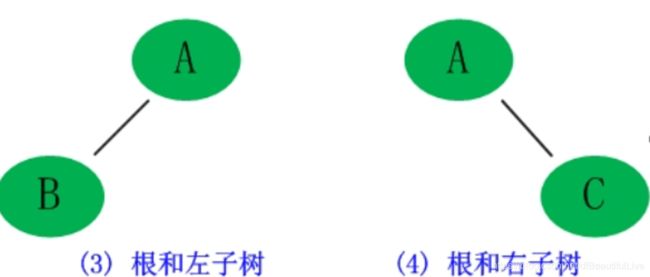
3.根的左子树为空
4. 根的右子树为空
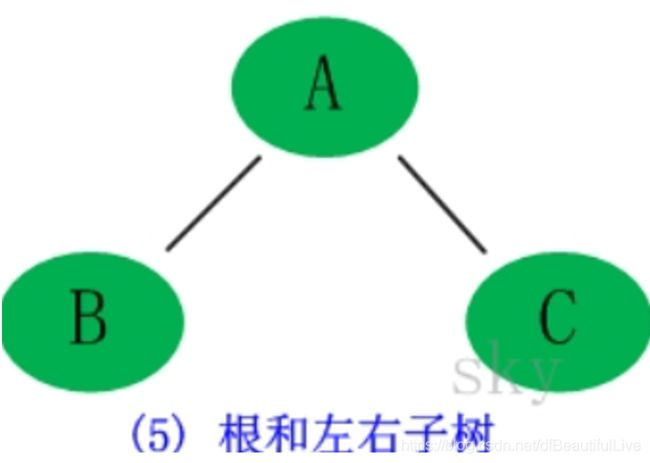
5.根和左、右两树
六、二叉树性质
性质1:二叉树第i层上的结点数目最多为2{i-1} (i≥1);
比如:第三层就是2*(3-1)=4那么第三层最多是4个节点,根节点从1开始算
性质2:深度为k的二叉树至多有2{k}-1个节点,(k≥1);
比如:深度为3那么就是2*2*2-1=7,那么层数为3的数,所有节点全下来最多有3个。
性质3:包含n个节点的二叉树的高度至少为log2 (n+1);(很少用,且实用意义不大)
七、二叉树分类
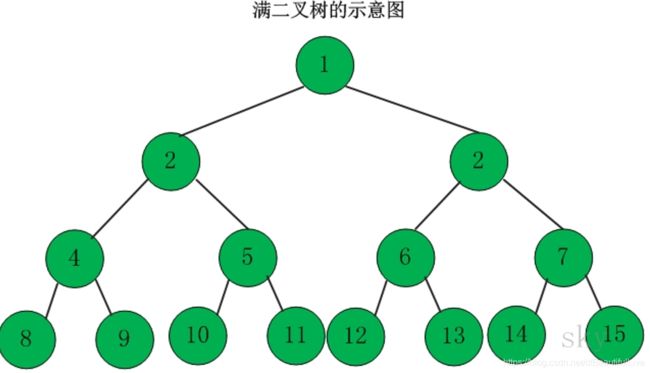
7.1 满二叉树
除最后一层无任何子节点外,每一层上的所有节点都有两个子节点的二叉树。也就是说一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就是满二叉树。如果这个二叉树高度为h,且节点总数是2{h} –1,则它就是满二叉树。
记住满二叉树简单的口令:父有两子,分列左右,左右满堂
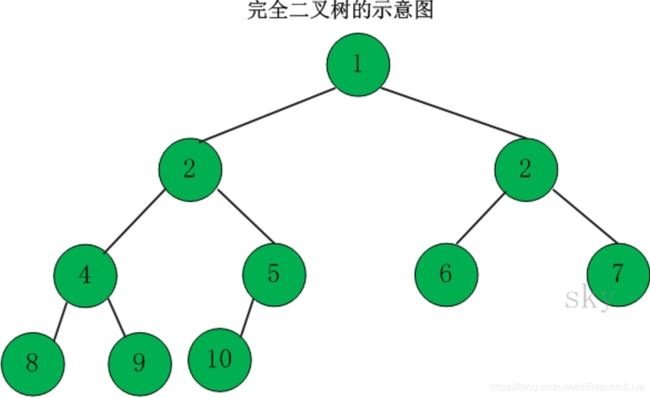
7.2 完全二叉树
完全二叉树是效率很高的数据结构。完全二叉树是由满二叉树引出来的。
叶子节点只能出现在最下层和次下层,且最下层的叶子节点集中在树的左部。显然,一颗满二叉树必定是一颗完全二叉树,而完全二叉树未必是满二叉树。
完全二叉树口令:父有两子,分列左右,最下次下,可无双子,最下叶节,必在左树。
7.3 二叉查找树(二叉搜索树)
- 若任意节点的左子树不空,则左子树上所有节点值均小于它的根节点的值;
- 任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点。
二叉查找树口令:父有两子,分列左右,左小右大,定无孪生。
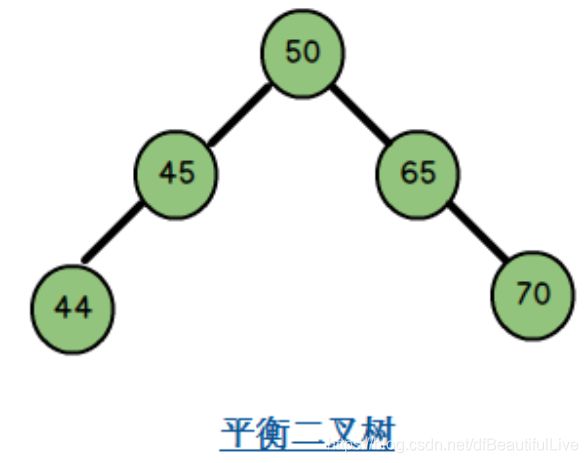
7.4 平衡二叉树
条件一:它必须是二叉查找树。
条件二:每个节点的左子树和右子树的高度差至多为1。
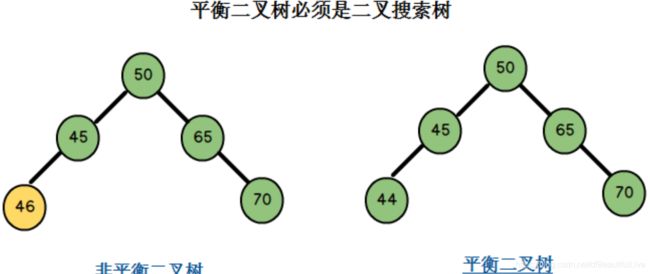
示例一:
图一中左边二叉树的节点45的左孩子46比45大,不满足二叉搜索树的条件,因此它也不是一棵平衡二叉树。
右边二叉树满足二叉搜索树的条件,同时它满足条件二,因此它是一棵平衡二叉树。
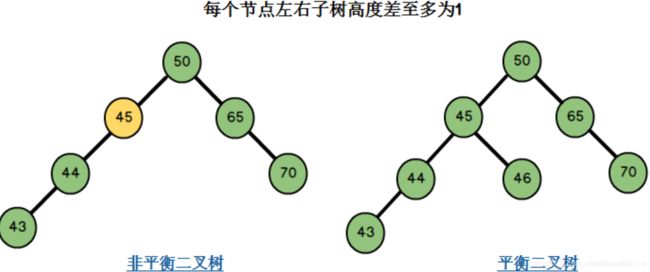
示例二:
左边二叉树的节点45左子树高度2,右子树高度0,左右子树高度差为2-0=2,不满足条件二;
右边二叉树的节点均满足左右子树高度差至多为1,同时它满足二叉搜索树的要求,因此它是一棵平衡二叉树。
AVL树的查找、插入、删除操作在平均和最坏的情况下都是O(logn),这得益于它时刻维护着二叉树的平衡。如果我们需要查找的集合本身没有顺序,在频繁查找的同时也经常的插入和删除,AVL树是不错的选择。不平衡的二叉查找树在查找时的效率是很低的。
八、二叉树与二叉搜索树的区别?
二叉树,每一个父节点下最多只能有两个节点,父节点与子节点(或者子树)有着一定的联系规则,这种规则不仅仅限制于排序规则。
二叉搜索树是二叉树的一种特殊二叉树,也是最常用的二叉树,二叉搜索树满足左子节点的关键字小于父节点,父节点的关键字小于或等于右子节点。所有的左子树节点的关键字值小于所有右子树的关键字值。也就是所谓的左小右大。这样有利于进行快速的数据处理。
九、二叉树的父、子节点之间一定要有某种联系规则么?
肯定的,试想,如果父节点与子节点之间,没有某种规则进行关联,随意的摆放,那二叉树就失去了原有的意义。
关联关系都是根据需求而定的,如果需要有序二叉树,就可以选择搜索二叉树。如果需要根据需求设定父子节点之间的联系,则需要从新定义二叉树父子节点之间的联系,如哈夫曼编码是根据字符出现频率和编码设定的父子节点关系。
十、二叉搜索树
10.1 二叉搜索树-查找
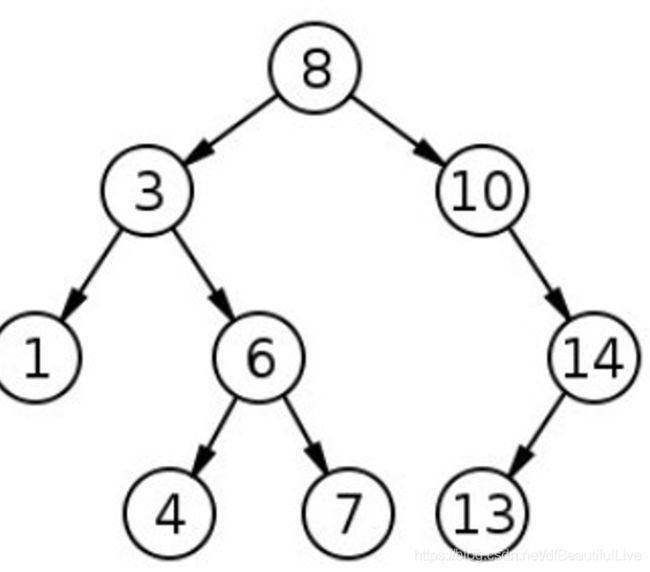
从根节点8开始,如果所查询的数字大于根节点,则像右子树查找。
如:查找13,根节点8,发现13大于8 –>查询右子节点10(比对13大于10)—>查询右子节点14(13小于14)-->查询左子节点-->返回结果。原则:左小右大
10.2 二叉搜索树-插入方式
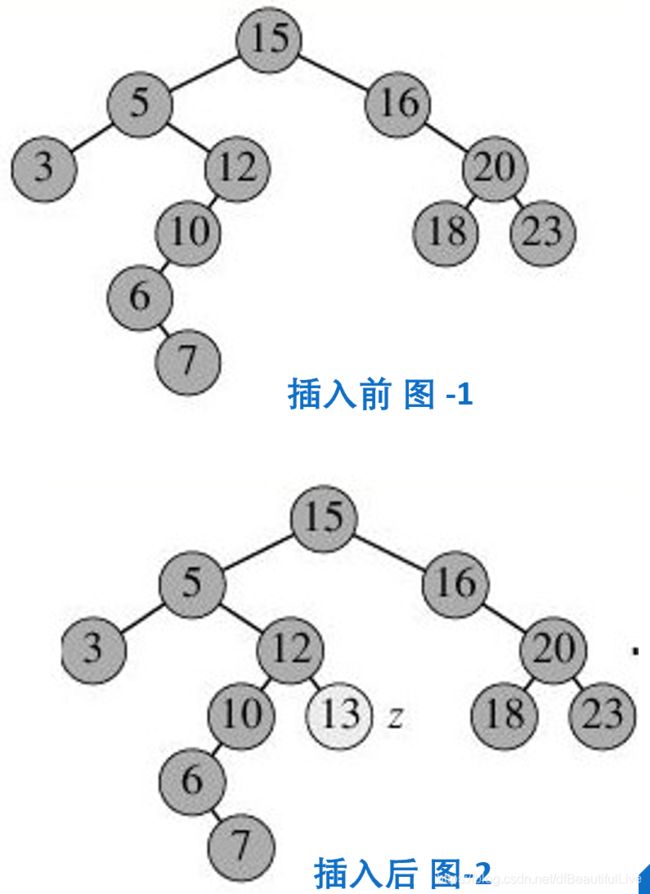
从根节点开始,如果插入的数字小于根节点,则向左子树寻找。
如:插入13,根节点15à查询左子节点5à查询右子节点12à查询右子节点为空à执行插入操作。和查找原理差不多,原则:左小右大。
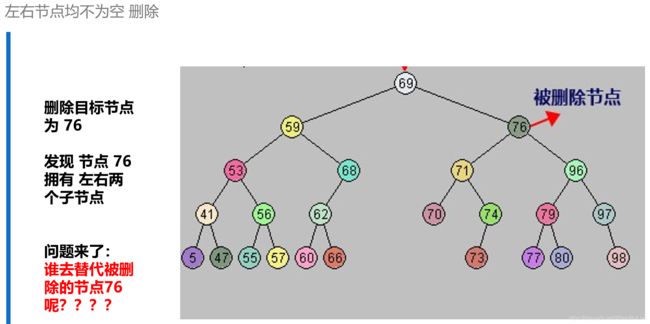
10.3 二叉树搜索树-删除
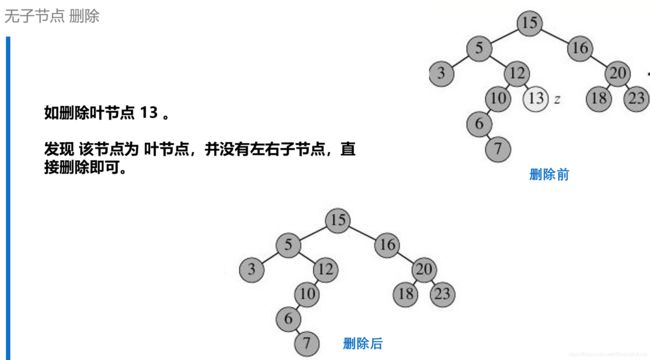
- 如果没有子节点:直接删除即可。
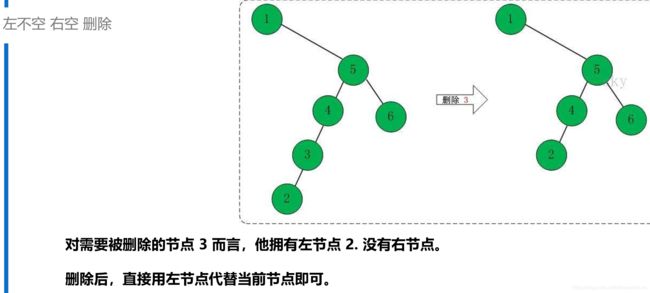
- 如果左不空,右空:用左子树代替当前节点即可。
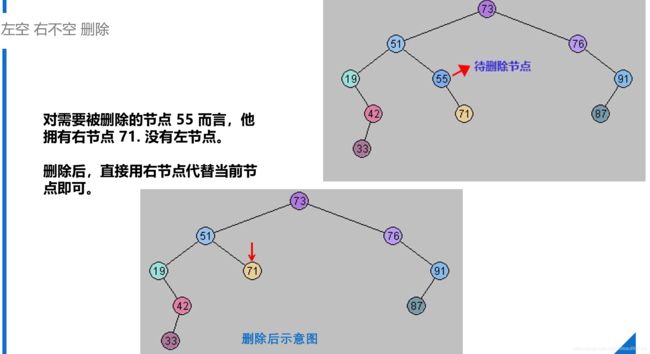
- 如果左空,右不空:直接用右子树代替当前节点即可。
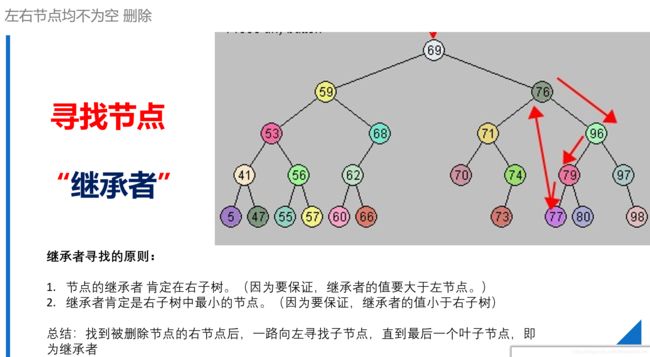
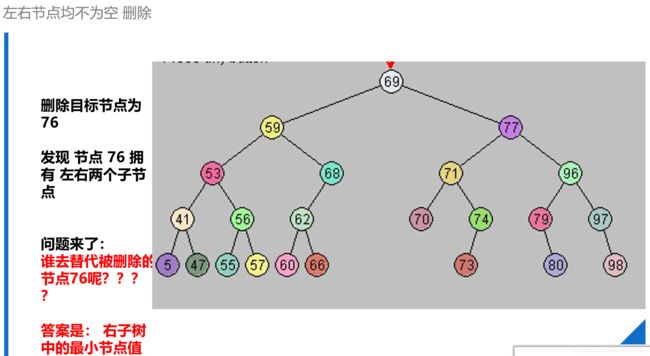
- 如果左右子节点均不为空:需要对右子树进行规则遍历,找到节点继承者
十一、二叉树遍历分类
先序遍历:遍历顺序规则为【根左右】
中序遍历:遍历顺序规则为【左根右】
后序遍历:遍历顺序规则为【左右根】
最常用的是:中序遍历(有序遍历),中序遍历出来的是一个有顺序的数据。
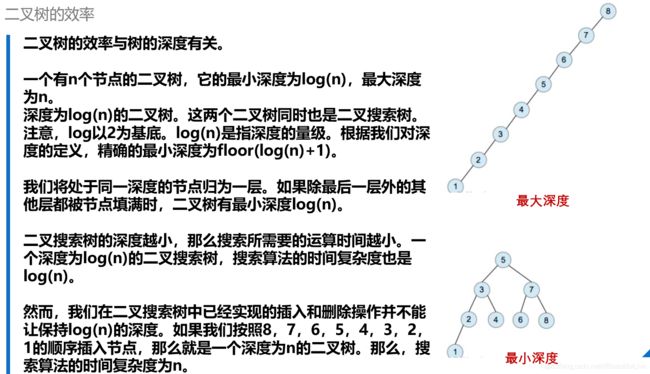
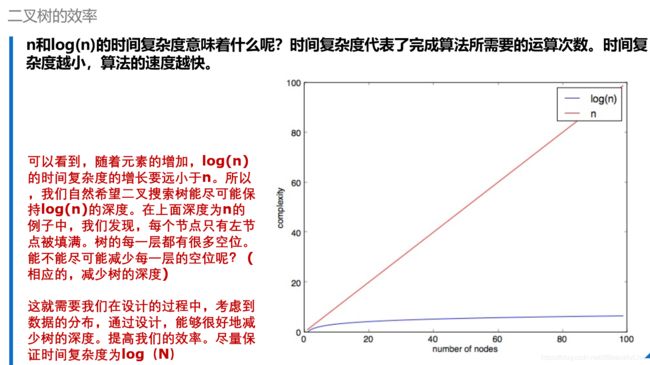
十二、二叉树的效率
总结:二叉树深度越大,查找遍历一就要一层一层去找,那么效率自然就不高,也失去了二叉树原本意义以及达到效率的效果
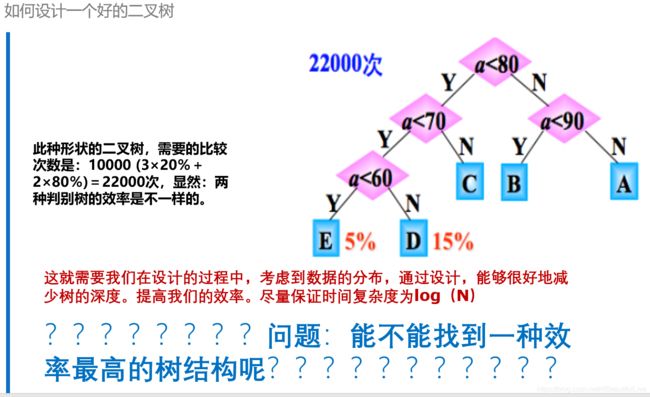
以下图片使用视频学习的课件
可以发现二叉树的设计不同,效率也就不同,最好的二叉树是左右节点都比较饱满的设计才是最高效的,那么引出一个最优二叉树-哈夫曼树,那么下章讲解
希望这篇二叉树介绍对想要吸取知识的你有帮助!