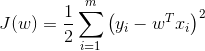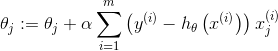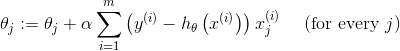优化算法-梯度下降法:BGD(批梯度)、SGD（随机梯度）、小批量梯度（MBGD）

（1）批梯度下降法（Batch Gradient Descent）

梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

损失函数表示如下：

                                                              

为了使得损失最小，先假定一个初始的权重值，用梯度下降法做迭代逼近，使最小。

                                                                       

其中α为步长（一般取0.001），为梯度。将带入上式有：

                                                     

                                                                 

 故 的更新为：

                                                                           

 上述推导仅针对一个样本进行的推导。若有m个样本，即为：

                                                                                                         （1）

            上述的梯度下降法为批梯度下降法。

             伪代码如下： {

                                                 

             }

从公式1，可以看出由于批梯度下降法需要遍历每一个样本求和，当样本数量较大时，它的效率是较低的。时间复杂度为。但也有它的优点：如果是凸函数，那么它得到的一定是全局最优解。

所以，又基于批梯度下降法（Batch Gradient Descent）改进后有了随机梯度下降法（Stochastic  /Incremental Gradient Descent）。随机梯度度下降法时间复杂度为。

（2）随机梯度下降法(Stochastic Gradient Descent)

随机梯度下降法也称为（incremental gradient descent）不同于批梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。

伪代码如下：

         （3）小批量梯度下降法（Mini-Batch Gradient Descent, MBGD）

小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用 ** batch_size** 个样本来对参数进行更新。

 

参考文献

[1]斯坦福大学机器学习视频以及讲义

[2]百度百科

[3]刘小朋友的PPT

[4]https://www.cnblogs.com/lliuye/p/9451903.html