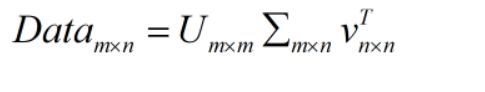基于SVD矩阵分解的用户商品推荐(python实现)
加粗样式## SVD矩阵分解
SVD奇异值分解
优点:简化数据,去除噪声,提高算法的结果
缺点:数据的转换可能难以理解
适用范围:数值性数据
其中
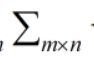
只有对角元素,是奇异值。奇异值中数值是按从大到小排列的,r个之后数值为0.。 这点高等数学里有。
如果我们把第二个奇异值矩阵中只保留一些值,把其他值全设为0.。从右到左重构数据即得到简化后的数据。
如奇异值数据中只保留最大2个奇异值,再重构数据。
可以认为原始数据去除了噪声。
python实现svd
import numpy as np
U,sigma,VT=np.linalg.svd([[1,1],[7,7]])
print('U:',U)
print('sigma:',sigma)
print('VT:',VT)
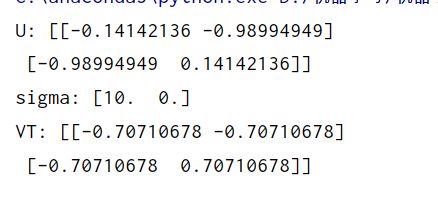
其中sigma以对角矩阵出现,我们需要记住它其实是个矩阵。
svd重构
import numpy as np
def loadExData():
return [[1,1,1,0,0],[2,2,2,0,0],[1,1,1,0,0],[5,5,5,0,0],[1,1,0,2,2],[0,0,0,3,3],[0,0,0,1,1]]
data=loadExData()
U,sigma,VT=np.linalg.svd(data)
print('U:',U)
print('sigma:',sigma)
print('VT:',VT)

可以发现sigma从大到小排列,如果我们只取前面3个奇异值。
则矩阵分解变成
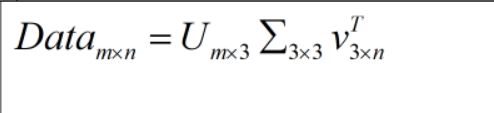
import numpy as np
def loadExData():
return [[1,1,1,0,0],[2,2,2,0,0],[1,1,1,0,0],[5,5,5,0,0],[1,1,0,2,2],[0,0,0,3,3],[0,0,0,1,1]]
data=loadExData()
U,sigma,VT=np.linalg.svd(data)
#重构实现
sig3=np.mat([[sigma[0],0,0],[0,sigma[1],0],[0,0,sigma[2]]])
#sig3=np.mat(np.eye(3)*sigma[:3])
print('sig3:',sig3)
data1=U[:,:3]*sig3*VT[:3,:]
print('重构后的数据',data1)
print('原始数据维度',np.array(data).shape)
print('重构后数据维度',np.array(data1).shape)
sig3=np.mat([[sigma[0],0,0],[0,sigma[1],0],[0,0,sigma[2]]])
sig3=np.mat(np.eye(3)*sigma[:3])

我们如何得知我们需要三个奇异值呀。
把奇异值求取平方和,将奇异值平方和累积到总值的0.9或者其他值即停止累积。即得到我们需要几个奇异值。
用户商品推荐
用户商品推荐在现实生活中有很多应用场景。比如如果你在今日头条上经常看某一类新闻,然后系统会经常给你推送该类新闻而不是其他类。
推荐算法:分为基于商品和基于用户。
基于商品:是比较商品之间的相似度,如果你喜欢某类电影,如果有一款新的电影出现啦,你还未看过,系统会计算该部电影与你看过的电影的相似度,如果相似度高则认为该类电影是你喜欢的,会把该类电影推送给你。
基于用户:计算不同用户之间的相似度,如果相似度高。会把其他用户看过的电影而你没有看过的电影推送给你。
1.相识度公式
欧式距离
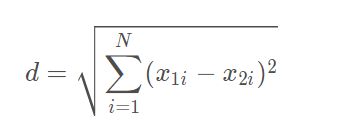
我们希望相似度在0到1之间,
可以用相似度=1/(1+距离)
from numpy import linalg as la
def ecludSim(inA, inB):
return 1.0 / (1.0 + la.norm(inA - inB))
皮尔逊相关系数
皮尔逊公式相比较于欧式距离有个优势:对数值的大小不敏感。比如一个极端值对某一商品打分为5分,而另一个则打1分,皮尔逊系数会认为两者是等价的。
皮尔逊系数是-1到1之间。我们希望得到的值是0到1之间。
所以0.5+0.5*皮尔逊系数
因为皮尔逊系数得到的是一个系数矩阵,我们只取一个值就可以啦,所以系数后面有[0][1]
from numpy import linalg as la
def pearsSim(inA, inB):
# 此时两个向量完全相关
return 0.5 + 0.5 * np.corrcoef(inA, inB, rowvar=0)[0][1]
余弦距离得到的值为-1到1,我们将其映射到0到1
from numpy import linalg as la
def cosSim(inA, inB):
num = float(inA.T * inB)
denom = la.norm(inA) * la.norm(inB)
return 0.5 + 0.5 * (num / denom)
2.基于用户和基于商品方法选择:
算法复杂度都会随着数量增加而增加。基于商品是商品增加复杂度增加,基于用户时用户数量增加而复杂度增加。对于绝大多数商店而言,用户数远远大于商品数,所以本文选择基于商品。
3.推荐流程
推荐系统的工作流程:给定一个用户,系统会为此用户返回N个最好的推荐菜。
(1):寻找用户没有评级打分的菜肴,即在用户-物品矩阵中的0值。
(2):在用户没有评级的所有物品中,对每个物品预计一个可能的评级分数。这就是说我们认为用户可能对物品的打分(这就是相似度计算的初衷)
(3):对这些物品的评分从高到底进行排序,返回前N 个商品。
4.原始数据
"""
函数说明:加载数据,菜肴矩阵
行:代表人
列:代表菜肴名词
值:代表人对菜肴的评分,0代表未评分
"""
def loadExData():
return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
[0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
[0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
[5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
[0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
[4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
[0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
[0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
[1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]
5.寻找两个用户都评级的物品
"""
Parameters:
dataMat - 训练数据集
user - 用户编号
simMeas - 相似度计算方法
item - 未评分的物品编号
Returns:
评分(0~5之间的值)
"""
def svdEst(dataMat, user, simMeas, item):
#假设user=1
# 得到数据集中的物品数目
n = np.shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 奇异值分解
# 在SVD分解之后,我们只利用包含90%能量值的奇异值,这些奇异值会以Numpy数组形式得以保存
U, Sigma, VT = la.svd(dataMat)
# 如果要进行矩阵运算,就必须要用这些奇异值构造出一个对角阵
Sig4 = np.mat(np.eye(4) * Sigma[: 4])
# 利用U矩阵将物品转换到低维空间中,构建转换后的物品(物品的4个主要特征)
xformedItems = dataMat.T * U[:, :4] * Sig4.I#shape(11,4)
# 遍历行中的每个物品(对用户评过分的物品进行遍历,并将它与其他物品进行比较)
for j in range(n):
userRating = dataMat[user, j]
# 如果某个物品的评分值为0,则跳过这个物品
if userRating == 0:
continue
# 相似度的计算也会作为一个参数传递给该函数
similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
print('商品 %d 和商品 %d 相似度similarity is: %f' % (item, j, similarity))
# 相似度会不断累加,每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度 userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
# 通过除以所有的评分和,对上述相似度评分的乘积进行归一化,使得最后评分在0~5之间,这些评分用来对预测值进行排序
else:
return ratSimTotal / simTotal
为了说明该函数功能,我们假设当前用户user=1,未评分商品为0
dataMat=np.mat(loadExData())
#假设当前用户时1
print('查看用户1未评级商品:',np.nonzero(dataMat[1, :].A == 0)[1])

# 得到数据集中的物品数目
n = np.shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 奇异值分解
# 在SVD分解之后,我们只利用包含90%能量值的奇异值,这些奇异值会以Numpy数组形式得以保存
U, Sigma, VT = la.svd(dataMat)
# 如果要进行矩阵运算,就必须要用这些奇异值构造出一个对角阵
Sig4 = np.mat(np.eye(4) * Sigma[: 4])
# 利用U矩阵将物品转换到低维空间中,构建转换后的物品(物品的4个主要特征)
xformedItems = dataMat.T * U[:, :4] * Sig4.I
print('降维重构后的数据:',xformedItems)
# 遍历行中的每个物品(对用户评过分的物品进行遍历,并将它与其他物品进行比较)
#假设未评分商品为第0个,开始计算
for j in range(n):
userRating = dataMat[1, j]
# 如果某个物品的评分值为0,则跳过这个物品
if userRating == 0:
continue
# 相似度的计算也会作为一个参数传递给该函数
similarity = cosSim(xformedItems[0, :].T, xformedItems[j, :].T)
print('商品 %d 和商品 %d 相似度is: %f' % (0, j, similarity))
# 相似度会不断累加,每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度 userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
print('商品0得分:',0)
# 通过除以所有的评分和,对上述相似度评分的乘积进行归一化,使得最后评分在0~5之间,这些评分用来对预测值进行排序
else:
print( '商品0得分:',ratSimTotal / simTotal)
通过此方法,我们可以给未知得分的商品0打上分啦。
xformedItems[0, :].T 这里有装置,我们采用的方法是基于商品。
简单说下该方法思路:
1.对于一个用户,找到他未打分的商品,和已打分过的商品。
2.计算未打分商品与已打分商品的相似度,这里的相似度计算输入的所有用户对该商品的打分。
3.将相似度乘以那个已打分的商品得分值。
4.求和 归一化 得到未打分商品的得分。未打分商品的得分主要贡献来源:未知商品与已打分商品相似度,已打分商品的得分

6.寻找前个未评级商品 推荐给用户
"""
函数说明:推荐引擎
Parameters:
dataMat - 训练数据集
user - 用户编号
N- 产生N个推荐结果
simMeas - 相似度计算方法
estMethod - 推荐引擎方法
Returns:
评分(0~5之间的值)
"""
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=svdEst):
# 寻找未评级的物品
# 对给定的用户建立一个未评分的物品列表
unratedItems = np.nonzero(dataMat[user, :].A == 0)[1]
# 如果不存在未评分物品,那么就退出函数
if len(unratedItems) == 0:
return ('本店所有商品你均尝试过,打过分')
# 物品的编号和评分值
itemScores = []
# 在未评分的物品上进行循环
for item in unratedItems:
estimatedScore = estMethod(dataMat, user, simMeas, item)
# 寻找前N个未评级的物品,调用svdEst()来产生该物品的预测得分,该物品的编号和估计值会放在一个元素列表itemScores中
itemScores.append((item, estimatedScore))
# 返回元素列表,第一个就是最大值
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[: N]
7.全部代码
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu
# @Date : 2020/8/22
import numpy as np
from numpy import linalg as la
#相似度
def cosSim(inA, inB):
num = float(inA.T * inB)
denom = la.norm(inA) * la.norm(inB)
return 0.5 + 0.5 * (num / denom)
#数据导入
"""
函数说明:加载数据,菜肴矩阵
行:代表人
列:代表菜肴名词
值:代表人对菜肴的评分,0代表未评分
"""
def loadExData():
return[[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
[0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
[0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
[5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
[0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
[4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
[0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
[0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
[1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]
"""
给未打分的商品打分
Parameters:
dataMat - 训练数据集
user - 用户编号
simMeas - 相似度计算方法
item - 未评分的物品编号
Returns:评分(0~5之间的值)
"""
def svdEst(dataMat, user, simMeas, item):
#假设user=1
# 得到数据集中的物品数目
n = np.shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 奇异值分解
# 在SVD分解之后,我们只利用包含90%能量值的奇异值,这些奇异值会以Numpy数组形式得以保存
U, Sigma, VT = la.svd(dataMat)
# 如果要进行矩阵运算,就必须要用这些奇异值构造出一个对角阵
Sig4 = np.mat(np.eye(4) * Sigma[: 4])
# 利用U矩阵将物品转换到低维空间中,构建转换后的物品(物品的4个主要特征)
xformedItems = dataMat.T * U[:, :4] * Sig4.I#shape(11,4)
# 遍历行中的每个物品(对用户评过分的物品进行遍历,并将它与其他物品进行比较)
for j in range(n):
userRating = dataMat[user, j]
# 如果某个物品的评分值为0,则跳过这个物品
if userRating == 0:
continue
# 相似度的计算也会作为一个参数传递给该函数
similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
print('商品 %d 和商品 %d 相似度similarity is: %f' % (item, j, similarity))
# 相似度会不断累加,每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度 userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
# 通过除以所有的评分和,对上述相似度评分的乘积进行归一化,使得最后评分在0~5之间,这些评分用来对预测值进行排序
else:
return ratSimTotal / simTotal
"""
函数说明:推荐引擎
Parameters:
dataMat - 训练数据集
user - 用户编号
N- 产生N个推荐结果
simMeas - 相似度计算方法
estMethod - 推荐引擎方法
Returns:
评分(0~5之间的值)
Modify:
2018-08-08
"""
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=svdEst):
# 寻找未评级的物品
# 对给定的用户建立一个未评分的物品列表
unratedItems = np.nonzero(dataMat[user, :].A == 0)[1]
# 如果不存在未评分物品,那么就退出函数
if len(unratedItems) == 0:
return ('本店所有商品你均尝试过,打过分')
# 物品的编号和评分值
itemScores = []
# 在未评分的物品上进行循环
for item in unratedItems:
estimatedScore = estMethod(dataMat, user, simMeas, item)
# 寻找前N个未评级的物品,调用svdEst()来产生该物品的预测得分,该物品的编号和估计值会放在一个元素列表itemScores中
itemScores.append((item, estimatedScore))
# 返回元素列表,第一个就是最大值
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[: N]
if __name__ == '__main__':
myMat = np.mat(loadExData())
recommend(myMat, 1, estMethod=svdEst)#对用户1进行推荐
print('\n----------------------------------------\n')
A = recommend(myMat, 1, estMethod=svdEst, simMeas=cosSim)
A=np.array(A)
for i in range(A.shape[0]):
print('给您推荐的商品是{},计算得分是{}'.format(A[i][0],A[i][1]))
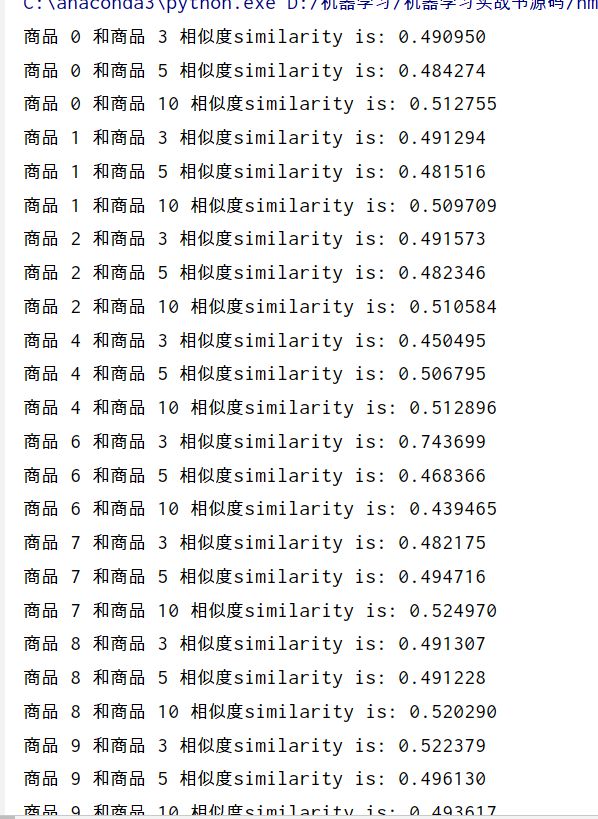
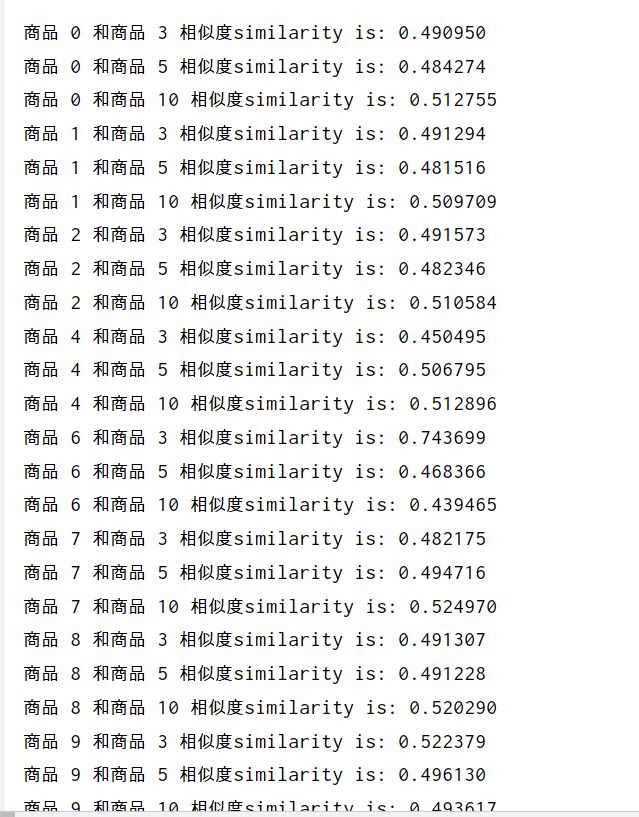
如果不使用SVD矩阵分解
未打分商品得分计算函数
"""
函数说明:基于物品相似度的推荐引擎
计算某用户未评分物品,以对该物品和其他物品评分的用户的物品相似度,然后进行综合评分
Parameters:
dataMat - 训练数据集
user - 用户编号
simMeas - 相似度计算方法
item - 未评分的物品编号
Returns:
评分(0~5之间的值)
Modify:
2018-08-08
"""
def standEst(dataMat, user, simMeas, item):
# 得到数据集中的物品数目
n = np.shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 遍历行中的每个物品(对用户评过分的物品进行遍历,并将它与其他物品进行比较)
for j in range(n):
userRating = dataMat[user, j]
# 如果某个物品的评分值为0,则跳过这个物品
if userRating == 0:
continue
# 寻找两个用户都评级的物品
# 变量overLap给出的是两个物品当中已经被评分的那个元素的索引ID
# logical_and计算x1和x2元素的逻辑与
overLap = np.nonzero(np.logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0]
print(dataMat[:, item].A)
# 如果相似度为0,则两者没有任何重合元素,终止本次循环
if len(overLap) == 0:
similarity = 0
# 如果存在重合的物品,则基于这些重合物重新计算相似度
else:
similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])
print('the %d and %d similarity is: %f' % (item, j, similarity))
# 相似度会不断累加,每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度 userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
# 通过除以所有的评分和,对上述相似度评分的乘积进行归一化,使得最后评分在0~5之间,这些评分用来对预测值进行排序
else:
return ratSimTotal / simTotal
电气专业的计算机萌新,写博文不容易,在大佬面前献丑啦。如果你觉得本文对你有用,请点个赞支持下,谢谢。