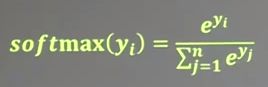| 一、均方误差损失函数 点击此处返回总目录 二、自定义损失函数 三、交叉熵损失函数 损失函数loss 就是前向传播计算出的结果(y)与已知标准答案(y_)的差距。 神经网络的优化目标就是想找到某套参数,使得推算出来的结果y与已知标准答案y_无限接近。也就是他们的差距loss最小。 主流的loss计算有三种: 均方误差mse(Mean Squared Error) 自定义 交叉熵ce(Cross Entropy) 一、均方误差 均方误差的定义和在TensorFlow中的表示如下:  我们用预测酸奶日销量的例子来理解损失函数。我们需要提前采集的数据有:一段时间内每天的x1因素、x2因素还有销量y_,作为数据集。这个数据集的量越大越好。我们知道了销量就可以预测产量了,我们想根据销量来看看生产多少,不希望生产多了,也不希望生产少了。 由于我们没有数据集,所以我们要制造一套数据集。随机生成数据集y_=x1+x2。为了更真实,还加了一个正负0.05的噪声。我们把这套自制的数据喂入神经网络,构建一个一层的神经网络,你和预测酸奶日销量的函数。  看下面的代码:
| #coding:utf-8
import numpy as np
import tensorflow as tf
SEED = 23455 #保证大家生成的一样,方便调试debug
BATCH_SIZE = 8 #一次喂入NN的一小撮特征是多少 #准备数据集
rdm = np.random.RandomState(SEED)
X=rdm.rand(32,2) #生成均匀分布的点。32行2列
Y_=[[x1+x2+rdm.rand()/10.0-0.05] for (x1,x2) in X] #(x1,x2)是每一行的两个值。生成的是一个列表。列表中有32行1列。
#rand()生成0~1.除10为[0,0.1)。减0.05为[-0.05,0.05)
#定义神经网络的参数、输入、输出、运算
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
W1=tf.Variable(tf.random_normal([2,1],stddev=1,seed=1)) y=tf.matmul(x,W1) #定义损失函数和反向传播算法
loss_mse=tf.reduce_mean(tf.square(y_-y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
#会话
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 20000
for i in range(STEPS):
start = (i*BATCH_SIZE)%32 #0,8,16,24,0,8,16,32...
end = start+BATCH_SIZE
sess.run(train_step,feed_dict={x:X[start:end],y_:Y_[start:end]})
if i%500 ==0:
print("After %d training steps,W1 is:" % (i))
print(sess.run(W1))
print("Final W1 is:")
print(sess.run(W1))
|
结果: After 0 training steps,W1 is:
[[-0.80974597]
[ 1.4852903 ]]
After 2000 training steps,W1 is:
[[0.08942621]
[1.673328 ]]
After 4000 training steps,W1 is:
[[0.4233252]
[1.4907392]]
After 6000 training steps,W1 is:
[[0.6173259]
[1.3329402]]
After 8000 training steps,W1 is:
[[0.74438614]
[1.2228196 ]]
After 10000 training steps,W1 is:
[[0.8294814]
[1.1482829]]
After 12000 training steps,W1 is:
[[0.88669145]
[1.0980824 ]]
After 14000 training steps,W1 is:
[[0.92517716]
[1.0643018 ]]
After 16000 training steps,W1 is:
[[0.95107025]
[1.0415728 ]]
After 18000 training steps,W1 is:
[[0.9684917]
[1.0262802]]
Final W1 is:
[[0.98019385]
[1.0159807 ]] 可以看到,两个参数都向着1,1趋近。最后拟合的结果是0.98x1+1.01x2,这一结果与生成的公式是一致的。 二、自定义损失函数 我们在刚才的例子中,使用了均方误差损失函数,默认认为预测多了或者预测少了,损失是一样的。 然而,真实情况是,预测多了就卖不出去,损失的是成本;预测少了就不够卖,损失的是利润。利润和成本往往不相等。在这种情况下,使用均方误差计算loss,是没法让利益最大化的。这个时候,我们可以使用自定义损失函数。 用自定义损失函数计算每一个结果y与标准答案y_产生的损失累积和。我们可以把损失定义为一个分段函数。如果预测的结果y小于标准答案y_,则预测少了,损失的是利润。损失为PROFIT*(y_-y)。同理,y预测多了,则损失的是成本,损失为COST*(y-y_)。  在TensorFlow中,我们用下面这个函数实现。(应该是COST*(y-y_)、PROFIT*(y_-y),少写了两个乘号。)  tf.where(tf.greater(y,y_),A,B)表示y大于y_么?如果大于则输出A这个式子,如果不成立则输出B这个式子。再用reduce_sum对所有的式子求和。 在预测酸奶这个例子中,如果成本1元,利润9元,预测少了损失利润9元,预测多了损失成本1元。预测少了损失大,我们希望预测得到函数尽量往多了预测。  我们看一下代码,用自定义函数拟合出来的酸奶销量的函数是什么样的。 //这个代码与上一个代码相比,只修改了损失函数。
| #coding:utf-8
import numpy as np
import tensorflow as tf
SEED = 23455 #保证大家生成的一样,方便调试debug
BATCH_SIZE = 8 #一次喂入NN的一小撮特征是多少 #准备数据集
rdm = np.random.RandomState(SEED)
X=rdm.rand(32,2) #生成均匀分布的点。32行2列
Y_=[[x1+x2+rdm.rand()/10.0-0.05] for (x1,x2) in X] #(x1,x2)是每一行的两个值。生成的是一个列表。列表中有32行1列。
#rand()生成0~1.除10为[0,0.1)。减0.05为[-0.05,0.05)
#定义神经网络的参数、输入、输出、运算
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
W1=tf.Variable(tf.random_normal([2,1],stddev=1,seed=1)) y=tf.matmul(x,W1) #定义损失函数和反向传播算法
#loss_mse=tf.reduce_mean(tf.square(y_-y))
COST = 1
PROFIT = 9
loss = tf.reduce_sum(tf.where(tf.greater(y,y_),COST*(y-y_),PROFIT*(y_-y))) #就该了这一句。
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
#会话
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 20000
for i in range(STEPS):
start = (i*BATCH_SIZE)%32 #0,8,16,24,0,8,16,32...
end = start+BATCH_SIZE
sess.run(train_step,feed_dict={x:X[start:end],y_:Y_[start:end]})
if i%2000 ==0:
print("After %d training steps,W1 is:" % (i))
print(sess.run(W1))
print("Final W1 is:")
print(sess.run(W1))
|
运行结果: After 0 training steps,W1 is:
[[-0.762993 ]
[ 1.5095658]]
After 2000 training steps,W1 is:
[[1.0179386]
[1.041272 ]]
After 4000 training steps,W1 is:
[[1.021926]
[1.04654 ]]
After 6000 training steps,W1 is:
[[1.0161575]
[1.0395166]]
After 8000 training steps,W1 is:
[[1.0233285]
[1.0468347]]
After 10000 training steps,W1 is:
[[1.01756 ]
[1.0398113]]
After 12000 training steps,W1 is:
[[1.0238953]
[1.044447 ]]
After 14000 training steps,W1 is:
[[1.0191677]
[1.046247 ]]
After 16000 training steps,W1 is:
[[1.0252978]
[1.0447416]]
After 18000 training steps,W1 is:
[[1.0205702]
[1.0465417]]
Final W1 is:
[[1.0225189]
[1.0416601]] 可见两个参数都大于1了。最后拟合的函数为1.02x1+1.04x2,模型确实都在尽量往多了预测。 三、交叉熵损失 交叉熵可以表征两个概率分布之间的距离。交叉熵越大,两个概率分布越远;交叉熵越小,两个概率分布越近。 交叉熵的计算方法如下:  y_表示标准答案的概率分布。y表示预测结果的概率分布。通过交叉熵的值,可以判断哪个预测结果与标准答案更接近。 我们用例子进一步理解交叉熵的计算过程。 标准答案的概率分布y_=(1,0), 有两个元素,表示是二分类。第一个元素为1,表示第一种情况发生的概率是100%,第2个元素为0,表示第二种情况发生的概率为0。 神经网络预测出了第一组概率分布y1,认为第一种情况发生的概率是60%,第二种情况发生的概率是40%。神经网络又预测出了第二组概率分布y2,认为第一种情况发生的概率是80%,第二种情况发生的概率是20%。他们哪一个更接近标准答案?人为直观看上去,y2与标准答案更接近。 计算机是这样量化的,通过交叉熵的计算公式,计算得到y1与标准答案的距离是0.222,y2与标准答案的距离是0.097。可见,计算机也认为y2与标准答案更接近。  在TensorFlow中,我们用下式计算交叉熵:  (***) (***) 其中,tf.clip_by_value(),对y的值做了限制。当y小于1*10^(-12) 时,为1*10^(-12),防止出现log 0的错误;当y>1时,为1。这是因为输入的数均满足概率分布,都是0和1之间的数,不可能大于1。 在实际操作中,为了让前向传播计算出的结果满足概率分布,也就是让n分类的n个输出每个都在[0,1]之间,且n个输出之和为1,引入了softmax()函数。  对于n分类,每次会有n个输出y1~yn。yn表示第n种情况出现的可能性大小。这n个输出经过softmax()函数后,就会符合概率分布了。 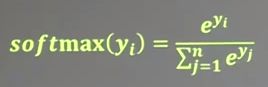 在TensorFlow里,提供了输出经过softmax函数使其满足概率分布后,再与标准答案求交叉熵的方法。我们在工程使用中,可以直接用一下两句话替换(***)式。它的输出就是当前计算出的预测值与标准答案的差距,也就是损失函数。我们在后面的手写体数字识别的例子中会直接使用这个函数。  |