树状数组 --算法竞赛专题解析（23）高级数据结构

本系列文章将于2021年整理出版。前驱教材：《算法竞赛入门到进阶》 清华大学出版社
网购：京东 当当   作者签名书：点我
公众号同步：算法专辑   
暑假福利：胡说三国
有建议请加QQ 群：567554289

   树状数组、线段树这两种数据结构用来解决一个常见的应用问题：高效率地查询和维护 前缀和(或者区间和)。
   所谓查询前缀和，即给出长度为n的数列 $A=a1,a2,...,an$和一个查询 $x\le n$，求 $sum(x)=a_1+...+a_x$。区间[i, j]的和可以通过前缀和求得： $a_i+...+a_j=sum(j)-sum(i-1)$。
   如果数列 $A$是静态不变的，代码很好写，预处理前缀和就好了，一次预处理的复杂度是O(n)的，然后每次查询都是O(1)的。但是，如果序列是动态变化的，例如改变其中一个元素 $a_k$的值，那么它后面的前缀和都会改变，需要重新计算，如果每次查询前元素都有变化，那么一次查询的的复杂度就变成了O(n)。
   有两种数据结构可以高效地处理这个问题： 树状数组、线段树。它们实现的两个功能：查询前缀和、修改元素值，复杂度都是 $O(logn)$的。
   在学习线段树和树状数组之前，读者可以自己思考如何实现用 $O(logn)$的复杂度实现查询和维护前缀和。思路并不难得到，根据二分法或者分治法，把整个数列分为两半，然后每部分再继续分为两半…这样一来，查询和修改都能以 $O(logn)$的复杂度得到解决。这就是线段树和树状数组的基本思路，线段树差不多重现了这个思路，而树状数组借助一个神奇的 $lowbit()$操作来简洁地实现。线段树的编码要更复杂一些，但是也更通用。
   本节介绍树状数组的概念和基本代码，然后给出它的经典应用：区间修改+单点查询、区间修改+区间查询、二维区间修改+区间查询、区间最值。

1. 思维导引

   树状数组（Binary Indexed Tree, BIT），从它的英文名可以看出，它是利用数的二进制特征进行检索的一种树状的结构。
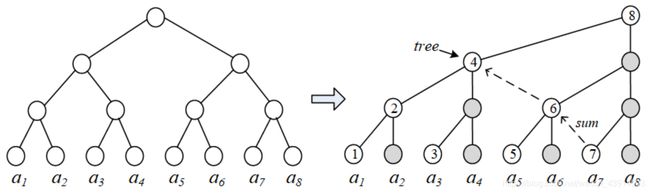
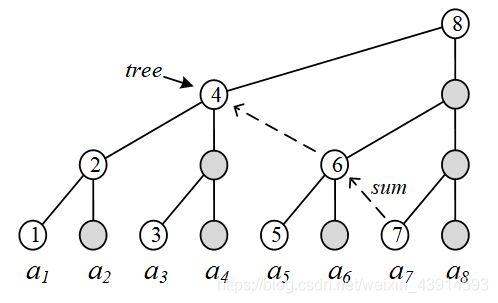
   如何利用二分的思想高效地求前缀和？以A = {$a_1,a_2,...,a_8$}这8个元素为例，左图是二叉树的结构，右边把它画成树状¹。

图1 从二叉树到树状数组

   右图圆圈中标记有数字的结点，存储的是称为树状数组的tree[]。一个结点上的tree[]的值，就是它树下的直连的子结点的和。例如$tree[1]=a_1，tree[2]=tree[1]+a_2，tree[3]=a_3，tree[4]=tree[2]+tree[3]+a_4，...，tree[8]=tree[4]+tree[6]+tree[7]+a_8$。
   利用tree[]，可以高效地完成下面两个操作：
   （1）查询，即求前缀和sum，例如：sum(8) = tree[8]，sum(7) = tree[7] + tree[6] + tree[4]，sum(6) = tree[6] + tree[4]。右图中的虚线箭头是计算sum(7)的过程。显然，计算的复杂度是O(logn)的，这样就达到了快速计算前缀和的目的。
   （2）维护。tree[]本身的维护也是高效的。当元素$a$发生改变时，能以$O(logn)$的高效率修改tree[]的值。例如更新了$a_3$，那么只需要修改tree[3]、tree[4]、tree[8]…，即修改它和它上面的那些结点：父结点（即$x+=lowbit(x)$）以及父结点的父结点。
   有了方案，剩下的问题是，如何快速计算出tree[]？观察查询和维护两个操作，发现：
   （1）查询的过程，是每次去掉二进制的最后的1。例如求sum(7) = tree[7] + tree[6] + tree[4]，步骤是：
   1）7的二进制是111，去掉最后的1，得110，即tree[6]；
   2）去掉6的二进制110的最后一个1，得100，即tree[4]；
   3）4的二进制是100，去掉1之后就没有了。
   （2）维护的过程，是每次在二进制的最后的1上加1。例如更新了a3，需要修改tree[3]、tree[4]、tree[]8…等等，步骤是：
   1）3的二进制是11，在最后的1上加上1得100，即4，修改tree[4]；
   2）4的二进制是100，在最后的1上加1，得1000，即8，修改tree[]8；
   3）继续修改tree[16]、tree[32]…等等。
   最后，树状数组归结到一个关键问题：如何找到一个数的二进制的最后一个1。

2. 神奇的lowbit(x)

  $lowbit(x)=x\&-x$，功能是找到$x$的二进制数的最后一个1。其原理是利用了负数的补码表示，补码是原码取反加一。例如$x=6=00000110_2，-x=x_{补}=11111010_2$，那么$lowbit(x)=x\&-x=10_2=2$。
  1~9的$lowbit$结果是：

x	1	2	3	4	5	6	7	8	9
x的二进制	1	10	11	100	101	110	111	1000	1001
lowbit(x)	1	2	1	4	1	2	1	8	1
tree[x]数组	tree[1] =a1	tree[2] =a1+a2	tree[3] =a3	tree[4] =a1+a2+a3+a4	tree[5] =a5	tree[6] =a5+a6	tree[7] =a7	tree[8] =a1 +…+a8	tree[9] =a9

  令$m=lowbit(x)$，定义$tree[x]$的值，是把$a_x$和它前面共$m$个数相加的结果，如上表所示。例如$lowbit(6)=2$，有$tree[6]=a_5+a_6$。
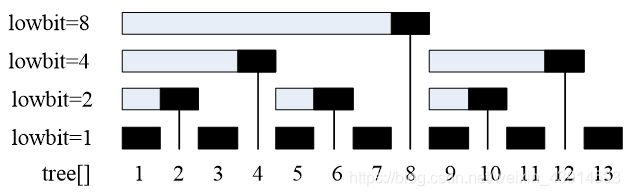
  $tree[]$是通过$lowbit()$计算出的树状数组，它能够以二分的复杂度存储一个数列的数据。 具体地，tree[x]中储存的是$[x-lowbit(x)+1,x]$中每个数的和。
  上面的表格可以画成下图。横线中的黑色表示$tree[x]$，它等于横线上元素相加的和。

图2 lowbit计算

3. 树状数组的概念和编码

  理解树状数组的原理之后，编码极其简洁，核心是$lowbit()$操作，计算得到树状数组$tree[]$，用于实现查询和维护前缀和。

#define lowbit(x)  ((x) & - (x))   
int tree[Maxn];
void update(int x, int d) {   //修改元素ax,  ax = ax + d
    while(x <= Maxn) {
        tree[x] += d;  
        x += lowbit(x); 
    }
}
int sum(int x) {           //返回值是前缀和：ans = a1 + ... + ax
    int ans = 0;
    while(x > 0){
        ans += tree[x];  
        x -= lowbit(x);
    }
    return ans;
}

  上述代码的使用方法是：
  （1）初始化。主程序先清空数组tree[]，然后读取$a_1，a_2，...，a_n$，用update()逐一处理这$n$个数，得到tree[]数组。代码中并不需要定义数组$a$，因为它隐含在$tree[]$中。
  （2）求前缀和。用$sum()$函数计算$a_1+a_2+...+a_x$。求和是基于数组tree[]的。
  （3）修改元素。执行$update()$，即修改数组$tree[]$。
  从上面的使用方法可以看出，$tree[]$这个数据结构可以用于记录元素，以及计算前缀和。
  值得注意的是，代码中并不需要定义和存储数组$a$，因为它隐含在$tree[]$中，用$sum()$函数计算$a_i=sum(i)-sum(i-1)$，复杂度$O(logn)$。

  下面介绍树状数组的经典应用，它们都结合了“差分数组”的概念，“差分数组”是用于区间查询的一个技巧。

4. 区间修改 + 单点查询

  一个序列$A=a1,a2,...,an$的更新（修改）有两种：
  （1）单点修改。一次改一个数；
   （2）区间修改。一次改变一个区间$[L,R]$内所有的数，例如把每个数统一加上$d$。
   树状数组的原始功能是“单点修改 + 区间查询”，是否能扩展为“区间修改”？只需一个简单而巧妙的操作（差分数组），就能把单点修改用来处理区间修改问题，实现高效的“区间修改 + 单点查询”，进一步也能做到“区间修改 + 区间查询”。
   下面的例题是典型的“区间修改 + 单点查询”。

---

Color the ball hdu 1556
问题描述：N个气球排成一排，从左到右依次编号为1, 2, 3 … N。每次给定2个整数L, R(L<= R)，lele从气球L开始到气球R依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第i个气球已经涂过几次颜色了，你能帮他算出每个气球被涂过几次颜色吗？
输入：每个测试实例第一行为一个整数N，(N <= 100000)。接下来的N行，每行包括2个整数L, R(1 <= L<= R<= N)。当N = 0，输入结束。
输出：每个测试实例输出一行，包括N个整数，第I个数代表第I个气球总共被涂色的次数。

---

  定义数组$a[i]$为气球$i$被涂色的次数。
  如果用暴力处理N次区间修改，是$O(N^2)$的。用树状数组，如果只是简单把区间$[L,R]$内的每个数$a[x]$用$update()$进行单点修改，复杂度更差，是$O(N^{2}logN)$的。下面把单点修改处理成区间修改，复杂度$O(NlogN)$。
  如何用树状数组处理区间修改？题目要求把$[L,R]$区间内每个数加上$d$，但是下面的解法不是对区间内每个数加$d$，而是操作一个被称为“差分数组”的$D$，它的定义是：
  $D[k]=a[k]-a[k-1]$，即原数组相邻元素的差。
  从定义可以推出：
    $a[k]=D[1]+D[2]+...+D[k]={\sum }_{i=1}^{k}D(i)$
  这个公式深刻地描述了$a$和$D$的关系，“差分是前缀和的逆运算”，它把求$a[k]$转化为求$D$的前缀和，前缀和正适合用树状数组来处理。
  对于区间$[L,R]$的修改问题，对$D$做以下操作：
  （1）把$D[L]$加上$d$；
  （2）把$D[R+1]$减去$d$。
  然后用树状数组函数$sum()$求前缀和$sum[x]=D[1]+D[2]+...+D[x]$，有：
  （1）$1\le x<L$，前缀和$sum[x]$不变；
  （2）$L\le x\le R$，前缀和$sum[x]$增加了$d$；
  （3）$R<x\le N$，前缀和$sum[x]$不变，因为被$D[R+1]$中减去的$d$抵消了。
  $sum[x]$的值与直接把$[L,R]$区间内每个数加上$d$得到的$a[x]$是相等的。这样，就利用树状数组高效地计算出了区间修改后的$a[x]$。

//hdu 1556代码
//tree[Maxn]，lowbit(x)，update()，sum()的代码前面已给出
const int Maxn = 100010;
int main(){
    int n;
    while(~scanf("%d",&n)) {  
        memset(tree,0,sizeof(tree));          //只需要一个tree[]数组
        for(int i=1;i<=n;i++) {               //区间修改
            int L, R; 
            scanf("%d%d",&L,&R);
            update(L,1);                       //本题的d = 1
            update(R+1,-1);
        }
        for(int i=1;i<=n;i++){                //单点查询
            if(i!=n)  printf("%d ",sum(i));   //把sum(i)看成a[i]
            else      printf("%d\n",sum(i));
        }
    }
    return 0;
}

  代码中的第一个$for$循环做了$n$次区间修改，复杂度$O(nlogn)$；第二个$for$循环做了$n$次单点查询，复杂度$O(nlogn)$。加起来总复杂度仍是$O(nlogn)$。

5. 差分数组

  hdu 1556这一题的思路借用了“差分数组”的概念。“差分数组”$D[]$是原数组$a[]$的一个辅助数组，$D[k]=a[k]-a[k-1]$，记录相邻元素之间的差值，它专用于“区间修改”这种题型。
  也可以直接用“差分数组”写代码，和上面树状数组的代码差不多。就本题的要求而言（打印所有气球，即输出所有的前缀和），“差分数组”的代码，复杂度比树状数组的代码还要好一些。

//hdu 1556 用差分数组求解
#include
using namespace std;
const int Maxn = 100010;
int a[Maxn],D[Maxn];               //a是气球，D是差分数组

int main(){
    int n;
    while(~scanf("%d",&n)) { 
        memset(a,0,sizeof(a)); memset(D,0,sizeof(D));
        for(int i=1;i<=n;i++){
            int L,R; scanf("%d%d",&L,&R);
            D[L]++;                 //差分，原理和前面树状数组一样
            D[R+1]--;
        }
        for(int i=1;i<=n;i++){
            a[i] = a[i-1] + D[i];          //求前缀和a[]，a[i]就是气球i的值
            if(i!=n)  printf("%d ", a[i]);  //逐个打印结果
            else      printf("%d\n",a[i]);
        }        
    }
    return 0;
}

  不过，遇到“区间修改”这种题型，还是建议用树状数组来求解。原因是差分数组对“区间修改”是很高效的，但是对“单点查询”并不高效。即使只查询一个前缀和，差分数组仍然要计算所有的前缀和，复杂度$O(n)$；而树状数组做一次前缀和计算是$O(logn)$的。

6. 区间修改 + 区间查询

  前面的例题完成的是“区间修改 + 单点查询”，下面考虑把单点查询扩展到区间查询，即查询的不是一个单点$a[x]$的值，而是区间$[i,j]$的和。
  仅仅用一个树状数组，无法同时高效地完成“区间修改”和“区间查询”，因为这个树状数组的tree[]已经用于“区间修改”，它用$sum()$计算了单点$a[x]$，不能再用于求$a[i]$~$a[j]$的区间和。
  读者可能想到再加一个树状数组，也许能接着高效地完成区间查询。但是如果这两个树状数组只是简单地一个做“区间修改”，一个做“区间查询”，合起来效率并不高。做一次长度为$k$的区间修改，计算区间内每个$a[x]$的复杂度是$O(logn)$的；如果继续用一个树状数组处理这$k$个$a[x]$，复杂度是$O(klogn)$的；做$n$次修改和询问，总复杂度$O(n^{2}logn)$。
  这两个树状数组需要紧密结合才能高效完成“区间修改 + 区间查询”，称为“二阶树状数组”，它也是“差分数组”概念和树状数组的结合。下面给出一个典型例题。

---

线段树1 洛谷P3372
问题描述：已知一个数列，进行两种操作：（1）把某区间每个数加上d；（2）求某区间所有数的和。
输入：第一行包含两个整数 n，m，分别表示该数列数字的个数和操作的总个数。第二行包含n个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。接下来m行每行包含3或4个整数，表示一个操作，具体如下：
（1）1 L R d：将区间[L, R]内每个数加上d。
（2）2 L R：输出区间[L, R]内每个数的和。
输出：输出包含若干行整数，即为所有操作（2）的结果。
$1\le n，m\le 10^5$，元素的值在$[-2^{63},2^{63})$内。

---

  操作（1）是区间修改，操作（2）是区间查询。
  首先，求区间和$sum(L,R)=a[L]+a[L+1]+...+a[R]=sum(1,R)-sum(1,L-1)$，问题转化为求$sum(1,k)$。
  定义一个差分数组$D$，它和原数组a的关系仍然是$D[k]=a[k]-a[k-1]$，有$a[k]=D[1]+D[2]+...+D[k]$，下面推导区间和，看它和求前缀和有没有关系，如果有关系，就能用树状数组。
$a_1+a_2+...+a_k$
$=D_1+(D_1+D_2)+(D_1+D_2+D_3)+...+(D_1+D_2+...+D_k)$
$=k\ast D_1+(k-1)\ast D_2+(k-2)\ast D_3+...+(k-(k-1))D_k$
$=k(D_1+D_2+...+D_k)-(D_2+2D_3+...+(k-1)D_k)$
$=k{\sum }_{i=1}^k{D}_i-{\sum }_{i=1}^k(i-1)D_i$
  这是求两个前缀和，用两个树状数组分别处理，一个实现$D_i$，一个实现$(i-1)D_i$。
  下面是“区间修改 + 区间查询”的代码，完全重现了上面推导出的结论。
  代码中的$update1()$和$update2()$、$sum1()$和$sum2()$几乎一样。也可以合起来写成$update1(llx,lld,intv)$的样子，用$v$来区分处理$tree1$和$tree2$。不过像下面这样分开写更清晰，编码更快。
  代码的复杂度是$O(mlogn)$。

#include
using namespace std;
#define ll long long
const int Maxn = 100010;
#define lowbit(x)  ((x) & - (x))   
ll tree1[Maxn],tree2[Maxn];         //2个树状数组

void update1(ll x,ll d){
	while(x<=Maxn){
		tree1[x]+=d;  x+=lowbit(x);
	}
}
void update2(ll x,ll d){
	while(x<=Maxn){
		tree2[x]+=d;  x+=lowbit(x);
	}
}
ll   sum1(ll x){
	ll ans = 0;
	while(x>0) {
		ans+=tree1[x];x-=lowbit(x);
	}
	return ans;
}
ll   sum2(ll x){
	ll ans = 0;
	while(x>0) {
		ans+=tree2[x];x-=lowbit(x);
	}
	return ans;
}

int main(){
    ll n, m; scanf("%lld%lld",&n,&m);
    ll old = 0, a;
	for (int i=1;i<=n;i++) {        
        scanf("%lld",&a);      //输入每个初始值
        update1(i, a-old);     //差分数组原理，初始化
        update2(i,(i-1)*(a-old));
        old = a;
    }
	while (m--){                     //m个操作
		ll q, L, R, d; 
        scanf("%lld",&q);
		if (q==1){                   //区间修改
            scanf("%lld%lld%lld",&L, &R, &d);
            update1(L,d);            //第1个树状数组
            update1(R+1,-d); 
            update2(L,d*(L-1));      //第2个树状数组
            update2(R+1,-d*R);       //d*R = d*(R+1-1)
        }
		else {                       //区间询问
            scanf("%lld%lld",&L,&R);
            printf("%lld\n",R*sum1(R)-sum2(R) - (L-1)*sum1(L-1)+sum2(L-1));
        } 
	}
	return 0;
}

7. 二维区间修改 + 区间查询

  前面的例题都是一维的，下面给出一个二维求“区间修改+区间查询”的例题。

---

上帝造题的七分钟 洛谷 P4514
输入：第一行是X n m，代表矩阵大小为n×m。从第二行开始到文件尾的每一行出现以下两种操作：
L a b c d delta 代表将(a,b),(c,d)为顶点的矩形区域内所有数字加上delta。
k a b c d 代表求(a,b),(c,d)为顶点的矩形区域内所有数字的和。
输出：针对每个k操作，输出答案。
输入样例：
X 4 4
L 1 1 3 3 2
L 2 2 4 4 1
k 2 2 3 3
输出样例：
12
注：1 ≤ n ≤ 2048, 1 ≤ m ≤ 2048, −500 ≤ delta ≤ 500, 操作不超过200000个,保证运算过程中及最终结果均不超过32位带符号整数类型的表示范围。

---

  本题需要用二维树状数组。二维的“区间修改+区间查询”，就是一维“区间修改+区间查询”的扩展，方法和推导过程类似。
  （1）二维区间修改

图2 二维差分数组的定义

  如何实现区间修改？需要结合二维的差分数组。定义一个二维的差分数组$D[i][j]$，它和矩阵元素$a[c][d]$的关系是：
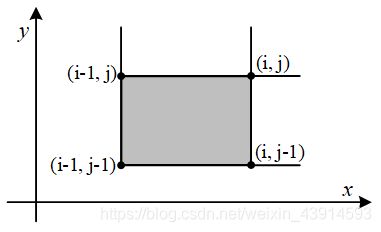
    $D[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]$，对照上图，$D[i][j]$就是阴影的面积。
    $a[c][d]={\sum }_{i=1}^c{\sum }_{j=1}^{d}D[i][j]$ ，看成对以$(1,1)、(c,d)$为顶点的矩阵内的$D[i][j]$求和。
  它们同样满足“差分是前缀和的逆运算”关系。
  用二维树状数组实现$D[i][j]$，编码见后面的代码中的$update()$和$sum()$。进行区间修改的时候，在$update()$中，每次第$i$行减少$lowbit(i)$，第$j$列减$lowbit(j)$，复杂度$O(lognlogm)$。
  （2）二维区间查询

图3 二维区间求和

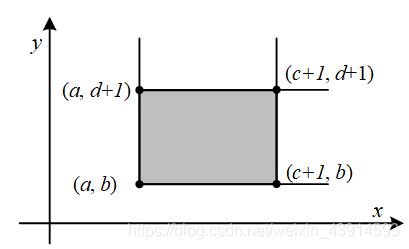
  查询(a, b)、(c, d)为顶点的矩阵区间和，对照上图的阴影部分，有：

  ${\sum }_{i=a}^c{\sum }_{j=b}^{d}a[i][j]={\sum }_{i=1}^c{\sum }_{j=1}^{d}a[i][j]-{\sum }_{i=1}^c{\sum }_{j=1}^{b-1}a[i][j]-{\sum }_{i=1}^{a-1}{\sum }_{j=1}^{d}a[i][j]+{\sum }_{i=1}^{a-1}{\sum }_{j=1}^{b-1}a[i][j]$

  问题转化为计算${\sum }_{i=1}^n{\sum }_{j=1}^{m}a[i][j]$，根据它和差分数组D的关系进行变换¹：

  ${\sum }_{i=1}^n{\sum }_{j=1}^{m}a[i][j]$
  $={\sum }_{i=1}^n{\sum }_{j=1}^m{\sum }_{k=1}^i{\sum }_{l=1}^{j}D[k][l]$
  $={\sum }_{i=1}^n{\sum }_{j=1}^{m}D[i][j]\times (n-i+1)\times (m-j-1)$
  $=(n+1)(m+1){\sum }_{i=1}^n{\sum }_{j=1}^{m}D[i][j]-(m+1){\sum }_{i=1}^n{\sum }_{j=1}^{m}D[i][j]\times i-(n+1){\sum }_{i=1}^n{\sum }_{j=1}^{m}D[i][j]\times j+{\sum }_{i=1}^n{\sum }_{j=1}^{m}D[i][j]\times i\times j$

  这是4个二维树状数组。
  下面的代码，重现了上面推理的结论。

#include
using namespace std;

const int N = 2050;
int t1[N][N],t2[N][N],t3[N][N],t4[N][N];
#define lowbit(x)  ((x) & - (x))  
int n,m; 
void update(int x,int y,int d){
	for(int i=x;i<=n;i+=lowbit(i))
		for(int j=y;j<=m;j+=lowbit(j)){
			t1[i][j] += d;
			t2[i][j] += x*d;
			t3[i][j] += y*d;
			t4[i][j] += x*y*d;
		}
}
int sum(int x,int y){
	int ans = 0;
	for(int i=x;i>0;i-=lowbit(i))
		for(int j=y;j>0;j-=lowbit(j))
			ans += (x+1)*(y+1)*t1[i][j] - (y+1)*t2[i][j] - (x+1)*t3[i][j] + t4[i][j];
	return ans;
}

int main(){
	char ch[2];	scanf("%s",ch);
    scanf("%d%d",&n,&m);     

	while(scanf("%s",ch)!=EOF){
        int a,b,c,d,delta;
        scanf("%d%d%d%d",&a,&b,&c,&d);
		if(ch[0]=='L'){
            scanf("%d",&delta);
			update(a,  b,   delta);    
            update(c+1,d+1, delta);
			update(a,  d+1,-delta); 
            update(c+1,b,  -delta);
		}
		else printf("%d\n",sum(c,d)+sum(a-1,b-1)-sum(a-1,d)-sum(c,b-1));
	}	
	return 0;
}

8. 偏序问题（逆序对 + 离散化）

  偏序问题：
   （1）一维偏序（逆序对）。给定数列a，求满足i < j且ai > aj的二元组(i, j)的数量。
   （2）二维偏序。给定n个点的坐标，求出满足xi < xj、yi < yj的二元组(i, j)的数量。
   （3）三维偏序。给定n个点的坐标，求满足xi < xj、yi < yj、zi < zj的二元组(i, j)的数量。
   逆序对问题有两种解法：归并排序、树状数组。用树状数组解逆序对又简单又巧妙，是树状数组应用的绝佳例子。

---

逆序对 洛谷 1908
题目描述：对于给定的一段正整数序列，逆序对就是序列中ai > aj且i < j的有序对。计算一段正整数序列中逆序对的数目。序列中可能有重复数字。
输入格式：第一行，一个数 n，表示序列中有 n个数。第二行n个数，表示给定的序列。序列中每个数字不超过 109。n <= 5×105。
输出格式：输出序列中逆序对的数目。
输入样例：
6
5 4 2 6 3 1
输出样例：
11

---

题解：直接用两重循环暴力搜，复杂度O(n2)。用树状数组，复杂度O(nlogn)。
   用树状数组解逆序对用到一个技巧：把数字看成树状数组的下标。每处理一个数字，树状数组的下标所对应的元素数值加一，统计前缀和，就是逆序对的数量。倒序或正序处理数据都行，下面是例子。
   （1）倒序。用树状数组倒序处理数列，当前数字的前一个数的前缀和即为以该数为较大数的逆序对的个数。例如样例的{5, 4, 2, 6, 3, 1}，倒序处理数字：
   1）数字1。把a[1]加一，计算a[1]前面的前缀和sum(0)，逆序对数量ans=ans+sum(0)=0；
   2）数字3。把a[3]加一，计算a[3]前面的前缀和sum(2)，逆序对数量ans=ans+sum(2)=1；
   3）数字6。把a[6]加一，计算a[6]前面的前缀和sum(5)，逆序对数量ans=ans+sum(5)=1+2=3；
   等等。
   （2）正序。正序，当前已经处理的数字个数减掉当前数字的前缀和即为以该数为较小数的逆序对个数。例如样例的{5, 4, 2, 6, 3, 1}，正序处理数字：
   1）数字5。把a[5]加一，当前处理了1个数，ans=ans+(1-sum(5))=0；
   2）数字4。把a[4]加一，当前处理了2个数，ans=ans+(2-sum(4))=0+1=1；
   3）数字2。把a[2]加一，ans=ans+(3-sum(2))=1+2=3；
   4）数字6。把a[6]加一，ans=ans+(4-sum(6))=3+0=3；
   等等。
   不过，上面的处理方法“把数字看成树状数组的下标”有个问题，如果数字比较大，例如数字等于109，那么树状数组的空间也要开到109 = 1G，这远远超过了题目限制的空间。用“离散化”这个小技巧能解决这个问题。
   所谓离散化，就是把原来的数字，用它们的相对大小来替换原来的数值，而它们的顺序仍然不变，不影响逆序对的计算。例如{1, 20000,10, 300, 890000000}，它们的相对大小是{1, 4, 2, 3, 5}，这两个序列的逆序对数量是一样的。前者需要极大的空间，后者空间很小。有多少个数字，离散化后开的空间就是多大。
   下面是洛谷 1908的代码，注意其中的离散化操作。离散化时计算“相对大小”需要用到排序，请仔细分析。

//lowbit(x)，update()，sum()的代码前面已给出
const int Maxn = 500010;
int tree[Maxn],rank[Maxn],n;
struct point{
  int num,val;
}a[Maxn];
bool cmp(point x,point y){
    if(x.val == y.val)   return x.num < y.num;  //注意：相等的情况，先出现标记更小
    return x.val < y.val;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) {
		scanf("%d",&a[i].val);
		a[i].num = i;         //记录顺序，用于离散化
	}
    sort(a+1,a+1+n,cmp);      //排序
    for(int i=1;i<=n;i++)     //离散化，得到新的数字序列rank[]
		rank[a[i].num]=i;     

	long long ans=0; 
    /*for(int i=1;i<=n;i++){    //正序处理
        update(rank[i],1);
        ans += i-sum(rank[i]);
    }*/
	for(int i=n;i > 0;--i){     //倒序处理
        update(rank[i],1);
        ans += sum(rank[i]-1);
    }
    printf("%lld",ans);
    return 0;
} 

9. 区间最值

  树状数组一般用来计算前缀和，不过，也能高效率地求区间最值，此时需要改写树状数组的代码。
  下面是一个“单点修改，区间最值”的例题。

---

I Hate It hdu 1754
题目描述：求区间内最大值。
输入：第一行是正整数N,M ( 0 Q A B 代表一个询问，询问从第A到第B个数字中的最大值。
U A B 代表一个更新，把第A个数字改为B。
输出：对每个询问，输出区间最大值。

---

  用暴力法，复杂度是O(MN)的。下面用树状数组求解。
  在标准的前缀和树状数组中，tree[x]中储存的是[x-lowbit(x)+1, x]中每个数的和。在求最值的树状数组中，tree[x]记录[x-lowbit(x)+1, x]内所有数的最大值。阅读下面内容时，请对照“树状数组原理图”。

图4 树状数组原理图

  （1）单点修改$update1(x,value)$。用$value$更新$tree[x]$的最大值，并更新树状数组上被它影响的结点。例如修改$x$ = 4，步骤是：
   1）修改$x$子树上直连的$tree[2]、tree[3]$；
   2）$x$的父结点$tree[8]$，以及$tree[8]$的直连子结点$tree[6]$、$tree[7]$；…等等。
   每一步复杂度是$O(logn)$，共$O(logn)$步，总复杂度是$O((logn{)}^2)$。注意一个特殊情况，初始化的时候需要修改所有n个数，复杂度$O(n(logn{)}^2)$，符合要求。

void update1(int x,int value){
	while(x <= n){
		tree[x] = value;
		for(int i=1; i<lowbit(x); i<<=1)      //用子结点更新自己
			tree[x] = max(tree[x], tree[x-i]);
		x += lowbit(x);                       //父结点
	}
}

  （2）区间最值查询query1()。区间 [L, R]的最值，分两种情况讨论。
  1）R - L >= lowbit( R)。对照“树状数组原理图”，即[L, R]范围包含了tree[R]直连子结点的个数，此时直接使用tree[R]的值：query1(L, R) = max(tree[R], query1(L, R−lowbit( R)))。
  2）当R - L < lowbit® 时，上述包含关系不成立，先使用a[R]的值，然后往前递推：query1(L, R) = max(a[R], query1(L, R−1))。
  query1()的复杂度仍然是$O((logn{)}^2)$。

int query1(int L,int R){
	int ans = 0;
	while(L<=R)	{
		ans = max(ans,a[R]);
		R--;
        while(R-L>=lowbit(R)){
            ans = max(ans,tree[R]);
            R-=lowbit(R);
        }
	}
	return ans;
}

  下面是hdu 1754的代码。

#include
using namespace std;
const int maxn=2e5+10; 
int n,m,a[maxn],tree[maxn]; 
int lowbit(int x){return x&(-x);}
void update1(int x,int value){;}    //代码在前面
int query1(int L,int R){;}          //代码在前面
int main(){
	while(~scanf("%d%d",&n,&m))	{
        memset(tree,0,sizeof(tree));
		for(int i=1; i<=n; i++){
			scanf("%d",&a[i]);
			update1(i,a[i]);
		}
		while(m--){
			char s[5];int A,B;
			scanf("%s%d%d",s,&A,&B);
			if(s[0]=='Q')
				printf("%d\n",query1(A,B));
			else{
				a[A]=B;
				update1(A,B);
			}
		}
	}
	return 0;
}

10. 离线处理

  最后给出一道经典题hdu 4630，它用到了“离线处理”的技术。

---

No Pain No Game hdu 4630
题目描述：给出一个序列，这个序列是1~n这n个数字的一个全排列。给出一个区间[L, R]，求区间内任意两个数的GCD（最大公约数）的最大值。
输入：第一行包括一个数T，后面有T个测试。每个测试的第一行是数字n，1<=n<=50000，第二行包括n个数，是1~n这n个数字的一个全排列。第三行包括数字Q，1<=Q<=50000，表示Q个询问。后面有Q行，每行有2个整数L，R，1<=L<=R<=n，表示一个询问。
输出：每个询问的结果打印一行。

---

题解：
  在区间[L, R]内，先求出区间内所有数的因子，出现2次的因子是公约数，最大的那个就是答案。
   有Q个区间询问，而Q很大，所以每次查询的复杂度需要达到$O(logn)$才行。但是如果对每个询问都单独计算这个区间内的最大公约数，最快也是$O(n)$的，Q个询问就是$O(n^2)$，超时。
   此时需要用离线处理，即先读取所有的询问，然后统一处理，计算结束后一起输出。
   前面的标准树状数组的代码，只能求区间和。能否改成求区间最值？把update()、sum()简单地改写成：

void update2(int x,int d){    
    while(x <= n){
        tree[x] = max(tree[x],d);  //改成：更新最大值
        x += lowbit(x);
    }
}
int query2(int x){              
    int ans = 0;
    while(x > 0){
        ans = max(ans,tree[x]);   //改成：求最大值
        x -= lowbit(x);
    }
    return ans;
}

   对照“树状数组原理图”，执行$update2(x,d)$的结果，是在$[x,n]$区间内，把$x$的父结点（即$x+lowbit(x)$,以及父结点的父结点）的$tree[]$值设置为$a_x$的最大值；执行$query2(x)$，返回的是$a_1{a}_x$的最大值。
   上述代码并不能用于上一小结的“求区间[L, R]最值”问题。因为最值没有前缀和的那种线性关系，[L, R]的最值与[1, L-1]、[1, R]的最值并没有关系。但是在本题中很有用。
   首先将所有的询问[L, R]按左端点L从大到小排序。从最大的L1开始计算，用$update2()$往父结点方向更新最大值，并用$query2(R1)$返回区间[L1, R1]的最大值，由于此时比L1小的那些询问还没有开始修改树状数组，也就不影响[L1, R1]的计算。下一步再从第二大的L2开始计算。在这个过程中，先计算的区间，能用于后计算的区间，从而提高了效率。

---

1. 参考https://www.cnblogs.com/lindalee/p/11503503.html ↩︎ ↩︎