Leetcode题解——单调栈问题
涉及到的题目:
739. 每日温度
42. 接雨水
84. 柱状图中最大的矩形
85. 最大矩形
496. 下一个更大元素 I
901. 股票价格跨度
402. 移掉K位数字
316. 去除重复字母(1081. 不同字符的最小子序列)
321. 拼接最大数
以上各题均可应单调栈来解决,减少时间和空间复杂度。
739. 每日温度
此题的暴力解法是从前向后遍历,但是这样的时间复杂读为O(n^2)。
而使用单调栈的思路为:
可以维护一个存储下标的单调栈,从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里,则表示尚未找到下一次温度更高的下标。
正向遍历温度列表。对于温度列表中的每个元素 T[i],如果栈为空,则直接将 i 进栈,如果栈不为空,则比较栈顶元素 prevIndex 对应的温度 T[prevIndex] 和当前温度 T[i],如果 T[i] > T[prevIndex],则将 prevIndex 移除,并将 prevIndex 对应的等待天数赋为 i - prevIndex,重复上述操作直到栈为空或者栈顶元素对应的温度小于等于当前温度,然后将 i 进栈。
为什么可以在弹栈的时候更新 ans[prevIndex] 呢?因为在这种情况下,即将进栈的 i 对应的 T[i] 一定是 T[prevIndex] 右边第一个比它大的元素,试想如果 prevIndex 和 i 有比它大的元素,假设下标为 j,那么 prevIndex 一定会在下标 j 的那一轮被弹掉。
由于单调栈满足从栈底到栈顶元素对应的温度递减,因此每次有元素进栈时,会将温度更低的元素全部移除,并更新出栈元素对应的等待天数,这样可以确保等待天数一定是最小的。
时间复杂度:O(n),其中 n 是温度列表的长度。正向遍历温度列表一遍,对于温度列表中的每个下标,最多有一次进栈和出栈的操作。
空间复杂度:O(n),其中 n 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
length = len(T)
ans = [0] * length
stack = []
for i in range(length):
while stack and T[i] > T[stack[-1]]:
ans[stack[-1]]= i - stack[-1]
stack.pop()
stack.append(i)
return ans42. 接雨水
算法
使用栈来存储条形块的索引下标。
遍历数组:
当栈非空且 height[current]>height[st.top()]
意味着栈中元素可以被弹出。弹出栈顶元素top。
计算当前元素和栈顶元素的距离,准备进行填充操作
distance=current−st.top()−1
找出界定高度
bounded_height=min(height[current],height[st.top()])−height[top]
往答案中累加积水量ans+=distance×bounded_height
将当前索引下标入栈
将 current 移动到下个位置
class Solution:
def trap(self, height: List[int]) -> int:
length = len(height)
if length < 3: return 0
res = 0
stack = []
for idx in range(length):
while stack and height[idx] > height[stack[-1]]:
top = stack.pop()
if len(stack) == 0:
break
h = min(height[stack[-1]], height[idx]) - height[top]
dist = idx - stack[-1] - 1
res += (dist * h)
stack.append(idx)
return res
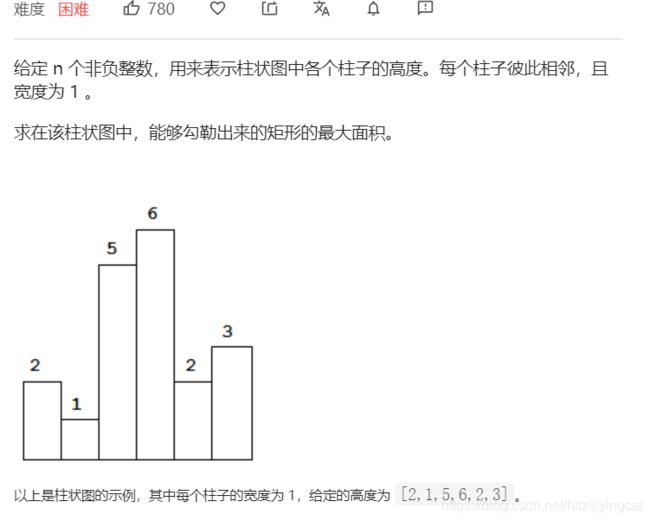
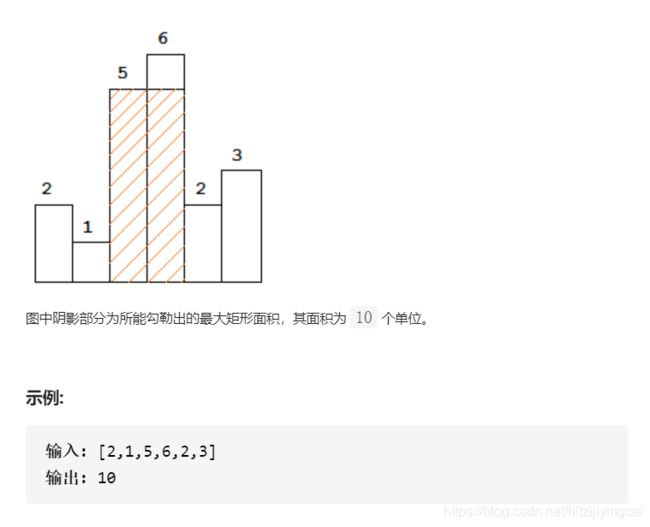
84. 柱状图中最大的矩形
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
area = 0
stack = []
heights = [0] + heights + [0]
length = len(heights)
for i in range(length):
while stack and heights[i] < heights[stack[-1]]:
tem = stack.pop()
area = max(area, heights[tem] * (i - stack[-1] - 1))
stack.append(i)
return area84题的变形即为85题:
85. 最大矩形
class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
# 定义最大矩形面积函数
def largeRectangle(arr):
arr = [0] + arr + [0]
stack = []
res = 0
for i in range(len(arr)):
while stack and arr[stack[-1]] > arr[i]:
tmp = stack.pop()
res = max(res, (i - stack[-1] -1) * arr[tmp])
stack.append(i)
return res
hight = [0] * len(matrix[0])
result = 0
for raw in range(len(matrix)):
for col in range(len(matrix[0])):
if matrix[raw][col] == '1':
hight[col] += 1
else:
hight[col] = 0
result = max(result, largeRectangle(hight))
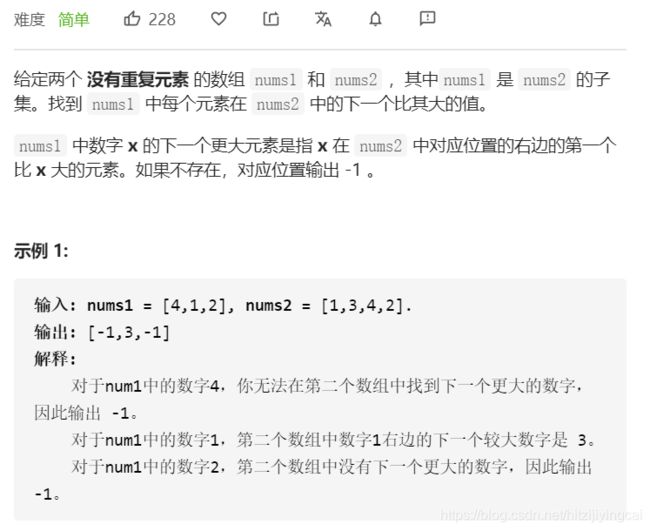
return result496. 下一个更大元素 I
思路:单调递减栈+哈希表
- 遍历nums2,维护一个递减栈
- 当得到一个更大的数的时候,将栈里小于它的数都放到哈希表当中
- 遍历nums1,对每一项查找哈希表,找到第一个比它大的数,并返回一个列表作为答案。如果在哈希表中不存在则返回默认值-1。
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
stack, mapping, res = list(), dict(), list()
for ii in nums2:
while stack and ii > stack[-1]:
mapping[stack.pop()] = ii
stack.append(ii)
for jj in nums1:
res.append(mapping.get(jj, -1))
return res901. 股票价格跨度
我们用单调栈维护一个单调递减的价格序列,并且对于每个价格,存储一个 weight 表示它离上一个价格之间(即最近的一个大于它的价格之间)的天数。如果是栈底的价格,则存储它本身对应的天数。例如 [11, 3, 9, 5, 6, 4, 7] 对应的单调栈为 (11, weight=1), (9, weight=2), (7, weight=4)。
当我们得到了新的一天的价格,例如 10,我们将所有栈中所有小于等于 10 的元素全部取出,将它们的 weight 进行累加,再加上 1 就得到了答案。在这之后,我们把 10 和它对应的 weight 放入栈中,得到 (11, weight=1), (10, weight=7)。
class StockSpanner(object):
def __init__(self):
self.stack = []
def next(self, price):
weight = 1
while self.stack and self.stack[-1][0] <= price:
weight += self.stack.pop()[1]
self.stack.append((price, weight))
return weight402. 移掉K位数字
以题目中的 num = 1432219, k = 3 为例,我们需要返回一个长度为 4 的字符串,问题在于: 我们怎么才能求出这四个位置依次是什么呢?
暴力法的话,我们需要枚举C_n^(n - k) 种序列(其中 n 为数字长度),并逐个比较最大。这个时间复杂度是指数级别的,必须进行优化。
一个思路是:
从左到右遍历
对于每一个遍历到的元素,我们决定是丢弃还是保留
问题的关键是:我们怎么知道,一个元素是应该保留还是丢弃呢?
这里有一个前置知识:对于两个数 123a456 和 123b456,如果 a > b, 那么数字 123a456 大于 数字 123b456,否则数字 123a456 小于等于数字 123b456。也就说,两个相同位数的数字大小关系取决于第一个不同的数的大小。
因此我们的思路就是:
从左到右遍历
对于遍历到的元素,我们选择保留。
但是我们可以选择性丢弃前面相邻的元素。
丢弃与否的依据如上面的前置知识中阐述中的方法。
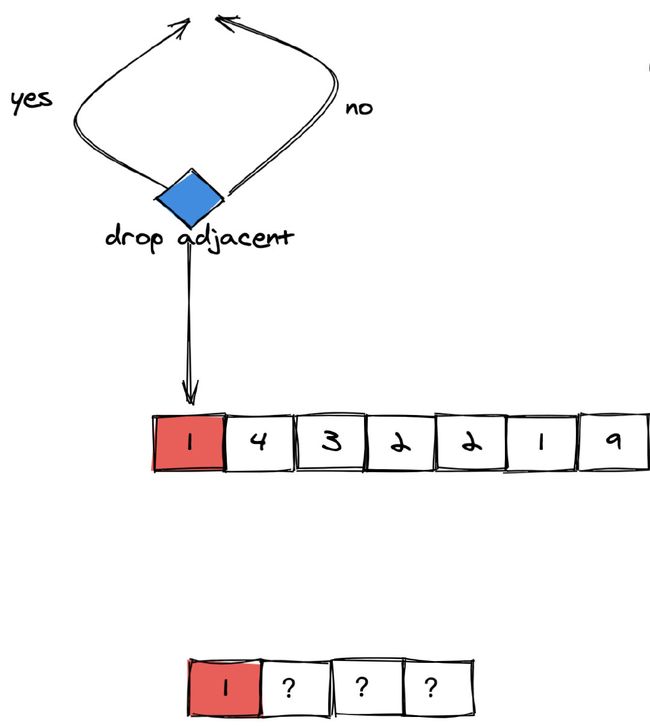
以题目中的 num = 1432219, k = 3 为例的图解过程如下:
由于没有左侧相邻元素,因此没办法丢弃。
由于 4 比左侧相邻的 1 大。如果选择丢弃左侧的 1,那么会使得剩下的数字更大(开头的数从 1 变成了 4)。因此我们仍然选择不丢弃。
由于 3 比左侧相邻的 4 小。 如果选择丢弃左侧的 4,那么会使得剩下的数字更小(开头的数从 4 变成了 3)。因此我们选择丢弃。
。。。
后面的思路类似,我就不继续分析啦。
class Solution(object):
def removeKdigits(self, num, k):
stack = []
remain = len(num) - k
for digit in num:
while k and stack and stack[-1] > digit:
stack.pop()
k -= 1
stack.append(digit)
return ''.join(stack[:remain]).lstrip('0') or '0'
注:如果题目改成求删除 k 个字符之后的最大数,我们只需要将 stack[-1] > digit 中的大于号改成小于号即可。
316. 去除重复字母 and 1081. 不同字符的最小子序列
注:这两题是一模一样的
与上一题目不同,这道题没有一个全局的删除次数 k。而是对于每一个在字符串 s 中出现的字母 c 都有一个 k 值。这个 k 是 c 出现次数 - 1。
沿用上面的知识的话,我们首先要做的就是计算每一个字符的 k,可以用一个字典来描述这种关系,其中 key 为 字符 c,value 为其出现的次数。
具体算法:
建立一个字典。其中 key 为 字符 c,value 为其出现的剩余次数。
从左往右遍历字符串,每次遍历到一个字符,其剩余出现次数 - 1.
对于每一个字符,如果其对应的剩余出现次数大于 1,我们可以选择丢弃(也可以选择不丢弃),否则不可以丢弃。
是否丢弃的标准和上面题目类似。如果栈中相邻的元素字典序更大,那么我们选择丢弃相邻的栈中的元素。
class Solution:
def removeDuplicateLetters(self, s: str) -> str:
remain = collections.Counter(s)
stack = []
for c in s:
if c not in stack:
while stack and c < stack[-1] and remain[stack[-1]] > 0:
stack.pop()
stack.append(c)
remain[c] -= 1
return ''.join(stack)321. 拼接最大数
和402题类似,只不不过这一次是两个数组,而不是一个,并且是求最大数。
最大最小是无关紧要的,关键在于是两个数组,并且要求从两个数组选取的元素个数加起来一共是 k。
然而在一个数组中取 k 个数字,并保持其最小(或者最大),和402题一样。但是如果问题扩展到两个,会有什么变化呢?
实际上,问题本质并没有发生变化。 假设我们从 nums1 中取了 k1 个,从 num2 中取了 k2 个,其中 k1 + k2 = k。而 k1 和 k2 这 两个子问题我们是会解决的。由于这两个子问题是相互独立的,因此我们只需要分别求解,然后将结果合并即可。
假如 k1 和 k2 个数字,已经取出来了。那么剩下要做的就是将这个长度分别为 k1 和 k2 的数字,合并成一个长度为 k 的数组合并成一个最大的数组。
class Solution:
def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:
def pick_max(nums, k): # 从nums里取出相对顺序不变的k个数构成的最大数
stack = []
drop = len(nums) - k
for num in nums:
while drop and stack and stack[-1] < num:
stack.pop()
drop -= 1
stack.append(num)
return stack[:k]
def merge(A, B): # 将nums1和nums2各自元素的相对顺序不变合并能产生的最大数
ans = []
while A or B:
bigger = A if A > B else B
ans.append(bigger[0])
bigger.pop(0)
return ans
max_ = []
for i in range(k+1): # 遍历所有组合方式,取最大的结果
if i <= len(nums1) and k-i <= len(nums2):
max_ = max(max_, merge(pick_max(nums1, i), pick_max(nums2, k-i)))
return max_