维纳滤波

之前所接触的低通/带通/高通滤波器和匹配滤波器等，都是应用于要求“最佳”系数不随时间变化的场合。但是，在通信、雷达、语音处理和生物医学等领域，通常需要滤波器系数能够根据输入信号进行自适应的调整。本文主要介绍FIR方式实现的维纳滤波器。

---

维纳滤波原理

维纳滤波器通常用于提取被噪声污染的有用信号，它是以最小均方误差准则进行滤波的，下面对该准则下的最优滤波器系数进行推导。

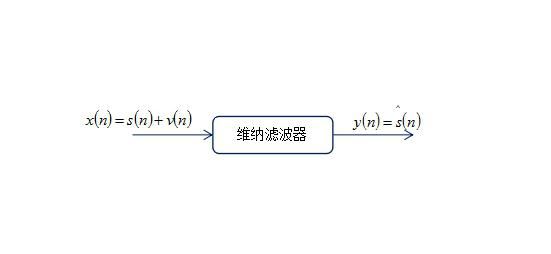
图1.1 维纳滤波器


如图1.1所示，输入 x(n) 中 s(n) 为有用信号， v(n) 为噪声干扰。输出 y(n) 为对有用信号 s(n) 的估计 s∧(n) 。
而 s(n) 是我们期望得到的信号，称之为期望信号。 s∧(n) 为滤波器实际输出的观测信号。那么误差定义应为：

e=s−s∧

均方误差为:

J=E(e2)

我们的目的就是要推导使 J 达到最小时的滤波器系数。

J=E{(s−s∧)2}  =E{(s−wHx)2}=E{s2−2swHx+wHxxHw}

其中 w 表示滤波器系数。
从上面式子可以看出， 代价函数/成本函数 J 是 w 的一个二次函数，在以 w 为坐标轴的坐标系中是一个凹函数，有唯一的一个极值点，只要求出该极值点，就可以得到使代价函数 J 最小的滤波器权值 w 。
令 J 对 w 求偏导：

∇=∂J∂wH=E{−2sx+2xHxw}

令其为 0 ，即可得到极值点：

wopt={E(xxH)}−1⋅E(dx)

其中 E(xxH) 为输入信号的自相关， E(dx) 为期望信号与输入信号的互相关。
通常写成更简洁的矩阵形式：

wopt=R−1xx⋅Rdx

由于实际中无法得到输入信号的理想统计参数，通常利用实际输入信号的采样来进行自相关系数矩阵和互相关系数矩阵的无偏估计。
该公式也称为维纳-霍夫方程，是最小均方误差准则下的滤波器系数最优解。

---

滤波器应用

维纳滤波器的应用十分广泛，总体上可以分为下面四类。

图2.1 维纳滤波器

下面分别对这四种情况进行介绍和仿真。

---

噪声抑制

这种应用较为常见，就是从噪声中提取有用信号，结构图如下：

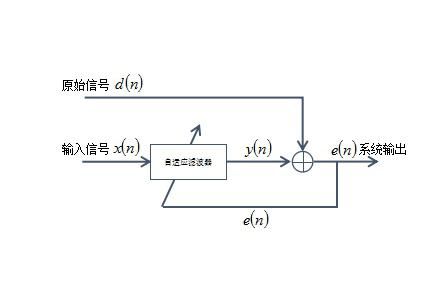
图2.2 噪声抑制

如图所示，原始信号 d(n) 就是包含了噪声干扰的有用信号，而输入信号 x(n) 是与 d(n) 中的噪声干扰相关的一个基准信号，通过维纳滤波器，利用基准信号 x(n) 对 d(n) 中的噪声干扰进行逼近，最后用原始信号减去滤波器输出即可得到估计的有用信号。
这里用电力线信号的传输作为例子，假设电力线中传递了一个编码信号，而除去信道噪声外，通常还有一个交流电 50Hz 的干扰，这时候就有必要对交流电干扰进行消除，下面是对该情形的仿真。
信道传输的信道编码信号如下所示

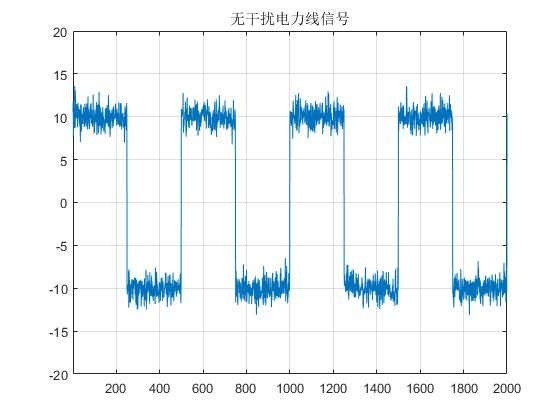
图2.3 电力线编码信号


添加 50Hz 交流电干扰信号

图2.4 带交流电干扰电力线编码信号


接下来采用一个两阶的维纳滤波器，进行自相关和互相关矩阵的计算，并进行滤波。

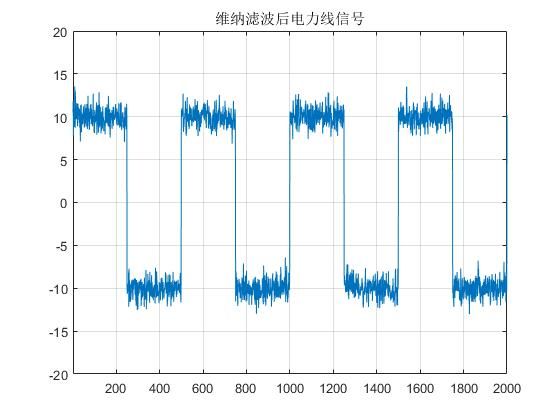
图2.5 滤波后的电力线信号


如图2.5所示，在仿真情况下信号得到了比较好的恢复。

---

代码附录

clc ; clear ; close all;

T = 10;    % 取10s信号进行分析
f0 = 50;   % 市电干扰频率
fs = 4*f0; % 采样频率

% generate observed signal 
for k = 1:1:T*fs
    if mod(floor(k/(T*fs/8)),2) == 0
        d(k) = 10;
    else
        d(k) = -10;
    end
end
d = d + normrnd(0,1,1,T*fs); % add noise

figure; plot(d); title('无干扰电力线信号'); grid on; axis([1 T*fs -20 20])

% add interference
n = 1:1:T*fs;
d = d + 50*cos(2*pi*f0*n/fs + pi/6); % pi/6 --- phase of interference

figure; plot(d); title('带市电干扰电力线信号');grid on; axis([1 T*fs -70 70])

% generate reference signal   order = 1  /  coeff number = 2
x_in1 = cos(2*pi*f0*n/fs);
x_in2 = cos(2*pi*f0*(n-1)/fs);
x = [x_in1;x_in2];

% wiener filter
R_xx = x*x'/(T*fs);     % E(xx')
R_dx = d*x'/(T*fs);     % E(dx')
w = R_xx\(R_dx.');
y = d - w'*x;

figure; plot(y); title('维纳滤波后电力线信号');grid on; axis([1 T*fs -20 20])

---

系统辨识

在系统辨识应用中，维纳滤波通常来确定未知系统的滤波器系数。系统辨识的结构如图

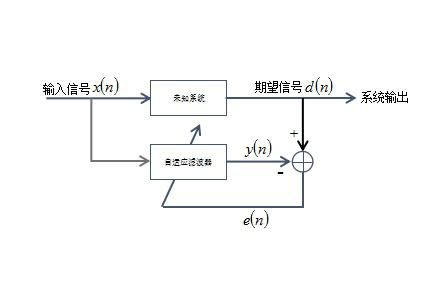
图2.6 系统辨识结构图

当然，在实际系统中，系统输出会带有信道噪声，自适应滤波器结构无法与未知系统完全匹配。
下面进行一个简单的仿真，假设输入信号 x(n) 为高斯白噪声，通过的未知系统为低通滤波器，利用滤波器输出 d(n) 和系统输入 x(n) 来对未知系统进行估计。
产生的高斯白噪声 x(n) 频谱：

图2.7 输入的高斯白噪声频谱

将该噪声通过未知系统（低通滤波器），得到的系统输出 d(n) 频谱为：

图2.8 系统输出的频谱

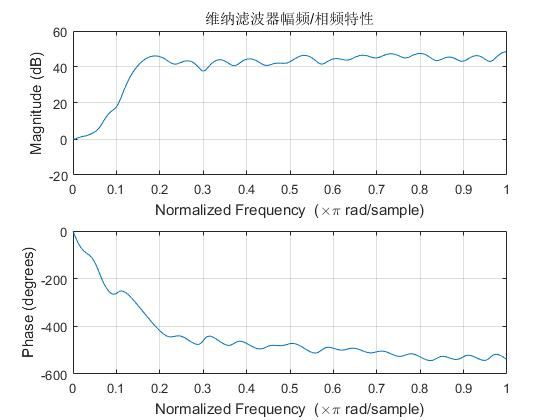
利用上面两个信号，构建维纳滤波器，得到维纳滤波器的系数幅频/相频特性为

图2.9 维纳滤波器幅频/相频特性

下面给出未知系统的幅频/相频特性，可以看出两者基本是一致的。

图2.9 未知系统幅频/相频特性

---

代码附录

% 系统辨识
clc ; clear ; close all;

x = normrnd(0,1,1,500); % input x(n)
b = fir1(31,0.05);      % fir filter coeff
d = filter(b,1,x);      % output d(n)

figure;    freqz(b);    title('未知系统幅频/相频特性')
figure;    plot(abs(fftshift(fft(x))));    title('输入信号x(n)')
figure;    plot(abs(fftshift(fft(d))));    title('未知系统输出d(n)')

x_in = zeros(32,500); % delay  0 to 31    filter order = 31
for k = 1:1:32
    x_in(k,:) = [zeros(1,k-1)  x(1:500-k+1)];
end

R_xx = x_in*x_in'/500;
R_dx = d*x_in'/500;
w = inv(R_xx)*R_dx.';
y = w'*x_in;

figure;    plot(abs(fftshift(fft(y))));  title('维纳滤波器输出信号频谱')
figure;    freqz(w);    title('维纳滤波器幅频/相频特性')

---

反演模拟

在反演模拟中，自适应滤波器的任务是提供表示未知的时变被控对象的最佳拟合的反演模型。它可用于滤波器的设计等场景中。具体结构如下图所示。

图2.10 反演模拟结构

输入信号 d(n) 进入未知系统，得到维纳滤波器的输入 x(n) ,而延迟后的输入信号 d(n) 2用于计算误差信号 e(n) ，最后得到的维纳滤波器的权值就是对未知系统的反演。
下面假设输入信号 d(n) 是高斯白噪声，未知系统为低通滤波器，未知系统的幅频/相频特性和得到的维纳滤波器的系数幅频/相频特性分别为。

图2.11 低通滤波器结构

得到的维纳滤波器的幅频/相频特性为

图2.12 维纳滤波器结构

---

代码附录

 clc ; clear ; close all;

d = normrnd(0,1,1,500);     % input d(n)
b = fir1(31,0.001);         % fir filter coeff
x = conv(d,b);              % output x(n)
figure;    freqz(b);    title('未知系统幅频/相频特性')
figure;    plot(abs(fftshift(fft(d))));    title('输入信号d(n)')
figure;    plot(abs(fftshift(fft(x))));    title('未知系统输出x(n)')
x_in = zeros(32,500); % delay  0 to 31    filter order = 31
for k = 1:1:32
    x_in(k,:) = [zeros(1,k-1) x(1:500-k+1) ];
end
d = [zeros(1,32) d(1:500-32) ]; % delay
R_xx = x_in*x_in'/500;
R_dx = d*x_in'/500;
w = inv(R_xx)*R_dx.';
y = w'*x_in;
figure;    plot(abs(fftshift(fft(y))));  title('维纳滤波器输出信号频谱')
figure;    fritle('维纳滤波器幅频/相频特性')

---

预测

当输入信号与白噪声有本质区别时，可将维纳滤波器作为预测器使用，结构如下图所示。

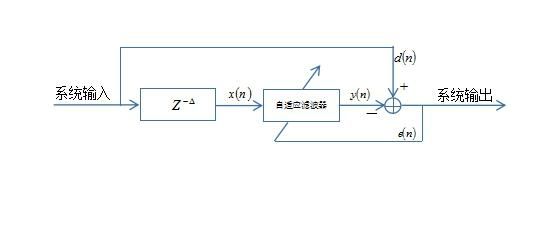
图2.13 预测器结构

下面用一个带高斯白噪声的正弦信号作为系统输入，用于实验维纳滤波的估计效果。
输入信号如下图

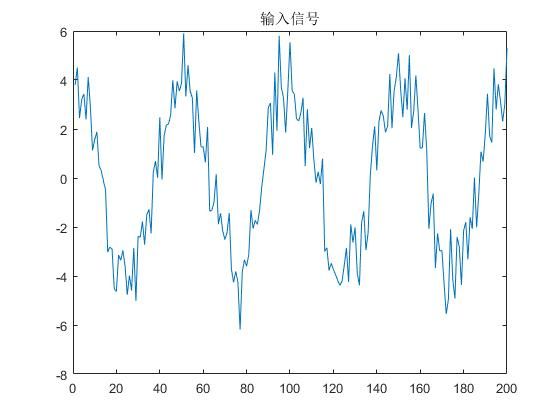
图2.13 预测器输入

预测器输出与输入对比

图2.14 预测器输入/输出对比

---

代码附录

clc ; clear ; close all;

f0 = 8;
fs = 400;
T = 0.5;
NUM = T*fs;
n = (1:1:NUM);
order = 32;

x = normrnd(0,1,1,NUM) + 4*cos(2*pi*f0*n/fs) ; % input
figure;    plot(x); title('输入信号')

x_in = zeros(order,NUM); % input x(n) delay 1 to order
for k = 1:1:order
    x_in(k,:) = [zeros(1,k) x(1:NUM-k) ];
end
R_xx = x_in*x_in'/NUM;
R_dx = x*x_in'/NUM;
w = inv(R_xx)*R_dx.';
y = w'*x_in;

figure; plot(n,x,'r',n,y,'-.b');legend('x(n)','y(n)'); title('输入输出对比')

---

参考资料：
[1] 《数字信号处理的FPGA实现（第三版）》U.Meyer-Baese著   刘凌译。