隐马尔可夫模型(Hidden Markov Model)
背景
隐马尔可夫模型(Hidden Markov Model)是一种常用的统计模型。应用也比较广泛,在时序问题,以及语音识别等问题上有广泛的应用。下面简单介绍一下隐马尔可夫模型。
隐马尔可夫模型是在马尔可夫过程的基础上,加入了隐含状态后的一种结构。这里首先介绍一下什么是马尔可夫过程(Markov Process)
在一个随机过程中,有一个状态变量 I I I,其下一时刻的状态之和之前的状态有关。例如布朗运动,粒子的下一时刻状态之和之前时刻的状态有关。而 I I I变化的过程,也就是马尔科夫链。这个约束,也就是马尔可夫假设。

在马尔可夫过程中,模型还是很复杂,我们还可以加约束来让模型变得简单一点。我们可以假设,状态变量 I I I的下一时刻状态只和上一时刻的状态有关。这样就得到了齐次马尔可夫模型。即:
p ( I t ∣ I t − 1 , I t − 2 , . . . , I 0 ) = p ( I t ∣ I t − 1 ) , t = 1 , 2 , . . . , T p(I_t|I_{t-1}, I_{t-2}, ..., I_{0}) = p(I_t|I_{t-1}), t=1, 2, ..., T p(It∣It−1,It−2,...,I0)=p(It∣It−1),t=1,2,...,T
我们可以看出,马尔可夫模型的描述,只针对某一个变量而言。但是实际生活中,很多变量之间都是相关的。例如你的运动是由肌肉的收缩和舒张来完成的。但是在观察者看来,你只是完成了一个简单的运动。其中,你的运动状态就是观测到的变化量,而肌肉的状态就是隐藏的状态。所以HMM模型的结构如下图所示:
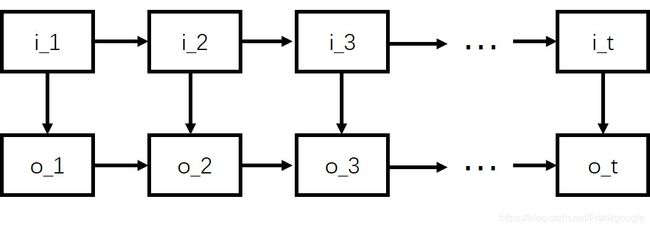
和马尔可夫过程一样,HMM也有一些约束条件。首先,HMM要满足马尔可夫假设且满足齐次马尔可夫模型,即:
p ( I t ∣ I t − 1 , o t − 1 , . . . , I 0 , o 0 ) = p ( I t ∣ I t − 1 ) , t = 1 , 2 , . . . , T p(I_t|I_{t-1}, o_{t-1}, ..., I_{0}, o_{0}) = p(I_t|I_{t-1}), t=1, 2, ..., T p(It∣It−1,ot−1,...,I0,o0)=p(It∣It−1),t=1,2,...,T
然后是观测独立性假设,也就是说任意时刻的观测值只依赖于当前时刻的马尔可夫链的状态 i t i_t it, 即:
p ( o t ∣ I t , I t − 1 , o t − 1 , . . . , I 0 , o 0 ) = p ( o t ∣ I t ) , t = 1 , 2 , . . . , T p(o_t|I_t, I_{t-1}, o_{t-1}, ..., I_{0}, o_{0}) = p(o_t|I_t), t=1, 2, ..., T p(ot∣It,It−1,ot−1,...,I0,o0)=p(ot∣It),t=1,2,...,T
原理
HMM的结构如上图所示,其中 I I I是状态变量, O O O是观测变量。假设 Q Q Q是所有可能的状态的集合, V V V是所有可能的观测的集合。
Q = { q 1 , q 2 , . . . , q N } Q = \{ q_1,q_2,...,q_N \} Q={q1,q2,...,qN}
V = { v 1 , v 2 , . . . , v M } V = \{v_1,v_2,...,v_M \} V={v1,v2,...,vM}
即可能的状态有N种, 可能的观测值有M种,两者不一定会相等。那么在一次试验中,观测到的值为 O O O,每个观测值会唯一对应一个状态值,因为试验已经结束了,假设状态序列为 I I I,那么 O O O和 I I I的长度一样,假设为T,那么: O = { O 1 , O 2 , . . . , O T } O = \{ O_1,O_2,...,O_T \} O={O1,O2,...,OT}
I = { I 1 , I 2 , . . . , I T } I = \{ I_1,I_2,...,I_T \} I={I1,I2,...,IT}
在 t t t时刻会有一个状态值,那么下一个时刻的状态值会与上一时刻相关,当然也可以是不相关的,由此给出状态矩阵 A A A的定义:
A = [ a i j ] A=[a_{ij}] A=[aij]
a i j a_{ij} aij表示当前时刻 t t t状态为 q i q_i qi的情况下,下一时刻的状态为 q j q_j qj的概率,这里 i , j = 1 , 2 , . . . N i,j=1,2,...N i,j=1,2,...N,用数学形式表示,即: a i j = P ( I t + 1 = q j ∣ I t = q i ) a_{ij}=P(I_{t+1}=q_j | I_t=q_i) aij=P(It+1=qj∣It=qi)
有了状态转移矩阵后,我们并不能直接估计下一时刻的状态,因为状态在整个试验过程中是隐藏的,试验中只能得到观测值的相关信息,所以还要有观测值和状态值之间的转换矩阵,即当观测到某个值时,其对应于各个状态的概率分别是多少。假设观测概率矩阵是 B B B,给出 B B B的定义:
B = [ b j k ] B=[b_{jk}] B=[bjk]
b j k b_{jk} bjk表示当前时刻 t t t状态值为 q j q_j qj的情况下,观测值为 v k v_k vk的概率。所以有 k = 1 , 2 , . . . M k=1,2,...M k=1,2,...M, j = 1 , 2 , . . . , N j=1,2,...,N j=1,2,...,N,用数学形式表示,即:
b j k = P ( o t = v k ∣ i t = q j ) b_{jk}=P(o_t=v_k | i_t=q_j) bjk=P(ot=vk∣it=qj)
确定了观测值和状态值之间的转换概率,当前时刻和下一时刻之间的状态转换概率,那么我们还需要确定可能的观测值在试验刚开始时被选中的概率,假设为 π \pi π,给出 π \pi π的定义:
π = [ π i ] \pi=[\pi_{i}] π=[πi]
其中 π i \pi_{i} πi表示观测值 q i q_i qi在刚开始被选中的概率,那么, i = 1 , 2 , . . . , N i=1,2,...,N i=1,2,...,N,用数学的形式表示,即:
π i = P ( I 1 = q i ) \pi_i=P(I_1=q_i) πi=P(I1=qi)
到这里,整个HMM模型中的主要参数已经全部介绍了,由介绍可知,根据 π , A , B \pi,A,B π,A,B可以让一个HMM模型顺利工作。可以求出在任意状态序列对应的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)。所以,我们也用这些参数来表示一个HMM模型,即: λ = { A , B , π } \lambda=\{ A,B,\pi \} λ={A,B,π} 。
常见问题
以上介绍了HMM的基本概念,在实际应用中,主要有以下几个基本问题:
- 已知模型 λ \lambda λ以及观测序列 O O O,计算在这种模型下出现这种观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
- 已知观测序列 O O O,但是不知道模型 λ \lambda λ,计算模型 λ \lambda λ,使得当前观测序列产生的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大
- 给定模型 λ \lambda λ和观测序列 O O O,计算最有可能产生这一观测序列的状态序列 I I I,即使得 P ( I ∣ O , λ ) 最 大 的 P(I|O,\lambda)最大的 P(I∣O,λ)最大的 I I I
以上就是最常见的HMM问题,主要涉及到模型中各个参数计算的问题。
在问题1中,我们需要计算观测序列出现的概率,主要可以用来判断出现的这一观测序列是否常见,如果计算得到的概率很低,但是在实际观测中却经常出现,那么就需要检查系统中是否出现了外部干扰。
在问题2中,我们需要计算模型的参数。主要是用于模型的学习和自适应参数调整的问题。模型是不确定的,但是根据给定的观测序列,我们需要找到一个最合适的模型,来保证出现这一观测序列的概率最大。有点类似回归求最优解或者神经网络拟合的思想。
在问题3中,我们需要通过观测序列和模型,来估计隐藏状态。这个主要适用于一些解码问题。通过观测值求解隐藏值。
针对以上的问题,分别有对应的解决办法。下面会介绍最常见的一些解法。当然,由于HMM中,观测变量和隐藏状态可能的取值是有限的。所以其实用穷举法也可以算,只是计算量会很大。
解决办法
问题1
已知模型和观测序列,要计算出现这种观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
这个问题有两种解法,前向和后向算法。两种方法比较类似。
- 前向算法
首先,我们定义一个概率:
p t ( i ) = P ( o 1 , o 2 , . . . , o t , I t = q i ) p_t(i) = P(o_1, o_2, ..., o_t, I_t=q_i) pt(i)=P(o1,o2,...,ot,It=qi)
p t ( i ) p_t(i) pt(i)表示观测序列为 o 0 , o 1 , . . . , o t {o_0, o_1, ...,o_t} o0,o1,...,ot,同时 I t = q i I_t=q_i It=qi的概率。所以我们有以下递推公式:
p t ( i ) = ( ∑ j = 1 N p t − 1 ( j ) a j i ) b i k p_{t}(i) = (\sum_{j=1}^{N}p_{t-1}(j)a_{ji})b_{ik} pt(i)=(j=1∑Npt−1(j)aji)bik
同时,有 o t = v k o_{t}=v_{k} ot=vk。在上面的公式中, ∑ j = 0 N p t − 1 ( j ) a j i \sum_{j=0}^{N}p_{t-1}(j)a_{ji} ∑j=0Npt−1(j)aji表示前 t − 1 t-1 t−1个输出为 o 1 , o 2 , . . . , o t − 1 {o_1, o_2, ..., o_{t-1}} o1,o2,...,ot−1,且第 t t t个隐藏状态为 q i q_i qi的概率。因为 t − 1 t-1 t−1时刻的状态是任何值都可以,只需要乘以对应的转移概率,就可以计算出 t t t时刻状态为 q i q_i qi的概率了。
然后在初始状态时,有:
p 1 ( i ) = π i b i k , o 1 = v k p_1(i) = \pi_ib_{ik}, o_1=v_k p1(i)=πibik,o1=vk
所以最终得到的概率为:
P ( O ∣ λ ) = ∑ i = 1 N p T ( i ) P(O|\lambda) = \sum_{i=1}^{N}p_T(i) P(O∣λ)=i=1∑NpT(i)
也就是说,在 T T T时刻,观测序列为 o 1 , o 2 , . . . , o T {o_1, o_2, ..., o_T} o1,o2,...,oT,且模型为 λ \lambda λ的概率为观测序列为 o 1 , o 2 , . . . , o T {o_1, o_2, ..., o_T} o1,o2,...,oT且 T T T时刻状态值为 q 1 , q 2 , . . . , q N {q_1, q_2, ..., q_N} q1,q2,...,qN的所有值的和。
- 后向算法
后向算法和前向算法比较类似,都是通过递推的方式逐步计算观测序列的概率。不同的地方是,后向算法是从后往前算,前向算法是从前往后算。
假设观测序列的长度为 T T T,并定义从 t + 1 t+1 t+1时刻到 T T T时刻的序列为 o t + 1 , o t + 2 , . . . , o T {o_{t+1}, o_{t+2}, ..., o_T} ot+1,ot+2,...,oT,且 t t t时刻的隐藏状态为 q i q_i qi的概率为:
p t ( i ) = P ( o t + 1 , o t + 2 , . . . , o T , I t = q i ∣ λ ) p_t(i) = P(o_{t+1}, o_{t+2}, ..., o_T, I_t=q_i|\lambda) pt(i)=P(ot+1,ot+2,...,oT,It=qi∣λ)
对于后向算法,初始状态应该是 p T ( i ) p_T(i) pT(i),表示的是观测序列为 o T + 1 {o_{T+1}} oT+1时,且隐藏状态为 q i q_i qi的概率,但是因为已经知道了 o T o_T oT的状态了,且 o T + 1 o_{T+1} oT+1并没有发生,所以这里其实给任意值都可以。这个值其实主要表示的是 T + 1 T+1 T+1时刻和 T T T时刻的关系,但是这个关系并不知道,所以给任意值都是可以的。表示这个关系可以是任意的。
然后和前向算法类似,我们可以计算后向的递推公式:
p t ( i ) = ∑ j = 1 N a i j b j k p t + 1 ( j ) p_t(i) = \sum_{j=1}^{N}a_{ij}b_{jk}p_{t+1}(j) pt(i)=j=1∑Naijbjkpt+1(j)
其中有, o t + 1 = v k o_{t+1} = v_k ot+1=vk
∑ j = 1 N a i j p t + 1 ( j ) \sum_{j=1}^{N}a_{ij}p_{t+1}(j) ∑j=1Naijpt+1(j)表示 t + 2 t+2 t+2时刻状态为 q j q_j qj且 t t t时刻的状态为 q i q_i qi的所有可能的 t + 2 t+2 t+2时刻的值的和,所以 a i j b j k p t + 1 ( j ) a_{ij}b_{jk}p_{t+1}(j) aijbjkpt+1(j)表示的是, t + 1 t+1 t+1时刻的观测值为 o t + 1 o_{t+1} ot+1,也就是 v k v_k vk,同时 t + 1 t+1 t+1时刻的状态值为 q j q_j qj的概率。求和之后就是, t + 1 t+1 t+1到 T T T时刻的观测值为 o t + 1 , o t + 2 , . . . , o T {o_{t+1}, o_{t+2}, ..., o_{T}} ot+1,ot+2,...,oT,且$
t 时 刻 的 隐 藏 状 态 为 时刻的隐藏状态为 时刻的隐藏状态为 q i q_i qi的概率。也就是 p t ( i ) p_t(i) pt(i)。
所以可以得到,最终计算的概率为:
P ( O ∣ λ ) = ∑ i = 1 N π i b i ( o 1 ) p 1 ( i ) P(O|\lambda) = \sum_{i=1}^{N}\pi_{i}b_i(o_1)p_1(i) P(O∣λ)=i=1∑Nπibi(o1)p1(i)
其中, p 1 ( i ) p_1(i) p1(i)表示的是观测序列为 o 2 , o 3 , . . . , o T {o_2, o_3, ..., o_T} o2,o3,...,oT,$ b_i(o_1)p_1(i) 表 示 观 测 序 列 为 表示观测序列为 表示观测序列为{o_1, o_2, …, o_T} 。 所 以 。所以 。所以\pi_ib_i(o_i)p_1(i) 表 示 观 测 序 列 为 表示观测序列为 表示观测序列为o_1, o_2, …, o_T , 且 , 且 ,且I_1=q_i 的 概 率 , 对 所 有 的 的概率,对所有的 的概率,对所有的I_1={q_1, q_2, …, q_N} 求 和 , 就 是 观 测 序 列 为 求和,就是观测序列为 求和,就是观测序列为{o_1, o_2, …, o_N}$的概率
以上就是两种计算观测序列概率的算法。主要的思想都是通过递推计算。
问题2
已知观测序列 O O O, 计算使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大的模型参数 λ \lambda λ
这个问题有点类似于回归问题中的拉格朗日极值问题,但是由于涉及到隐藏变量的极大似然估计,所以这里并不能用求导的方法来计算。广泛使用的一种计算方法是EM(Expectation Maximum)算法。关于EM算法,会在后续的文章中介绍,这里暂且不写。
问题3
已知观测序列 O O O和模型参数 λ \lambda λ,求可能产生这一观测序列的隐藏状态 I I I, 使得 P ( I ∣ λ ) P(I|\lambda) P(I∣λ)最大
这个问题类似于常见的解码问题。对于HMM模型下的解码问题,一般是用动态规划的方法来求解的。因为这样计算量会降低。常用的HMM解码问题的解决办法是维特比算法(Viterbi Algorithm)。这个也会在后续的文章中介绍。这里暂且不写。