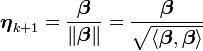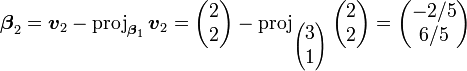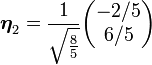格拉姆－施密特正交化Gram-Schimidt
格拉姆－施密特正交化
| 线性代数 | ||||||
|
||||||
矢量 · 矩阵 · 行列式 · 线性空间
|
||||||
在线性代数中，如果内积空间上的一组矢量能够张成一个子空间，那么这一组矢量就称为这个子空间的一个基。Gram－Schmidt正交化提供了一种方法，能够通过这一子空间上的一个基得出子空间的一个正交基，并可进一步求出对应的标准正交基。
这种正交化方法以Jørgen Pedersen Gram和Erhard Schmidt命名，然而比他们更早的拉普拉斯（Laplace）和柯西（Cauchy）已经发现了这一方法。在李群分解中，这种方法被推广为岩泽分解（Iwasawa decomposition）。
在数值计算中，Gram－Schmidt正交化是数值不稳定的，计算中累积的舍入误差会使最终结果的正交性变得很差。因此在实际应用中通常使用豪斯霍尔德变换或Givens旋转进行正交化。
目录[隐藏]
|
[编辑] 记法
：维数为n 的内积空间 
：中的元素，可以是矢量、函数，等等 
：
与
的内积 
：、……
张成的子空间 
：
在
上的投影
[编辑] 基本思想
在
上投影，构造
上的正交基
Gram-Schmidt正交化的基本想法，是利用投影原理在已有正交基的基础上构造一个新的正交基。
设
。
是上的
维子空间，其标准正交基为，且不在上。由投影原理知，与其在上的投影
之差
是正交于子空间的，亦即正交于的正交基
。因此只要将单位化，即
那么就是在上扩展的子空间
的标准正交基。
根据上述分析，对于矢量组
张成的空间
(
)，只要从其中一个矢量（不妨设为）所张成的一维子空间
开始（注意到就是的正交基），重复上述扩展构造正交基的过程，就能够得到 的一组正交基。这就是Gram-Schmidt正交化。
[编辑] 算法
首先需要确定已有基底矢量的顺序，不妨设为
。Gram-Schmidt正交化的过程如下：
 |
 |
||
 |
 |
||
 |
 |
||
 |
|
||
 |
 |
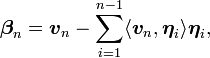这样就得到
上的一组正交基
，以及相应的标准正交基
。
- 例
考察如下欧几里得空间Rn中矢量的集合，欧氏空间上内积的定义为<a, b> = bTa：
下面作Gram－Schmidt正交化，以得到一组正交矢量：
下面验证矢量
与的正交性：
将这些矢量单位化：
于是
就是 
的一组标准正交基底。
[编辑] 不同的形式
随着内积空间上内积的定义以及构成内积空间的元素的不同，Gram-Schmidt正交化也表现出不同的形式。
例如，在实矢量空间上，内积定义为：
在复矢量空间上，内积定义为：
函数之间的内积则定义为：
与之对应，相应的Gram－Schmidt正交化就具有不同的形式。
[编辑] 参见
- 内积空间
- 内积
- 正交
- QR分解
- 线性代数