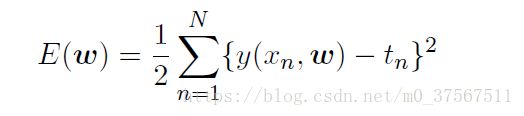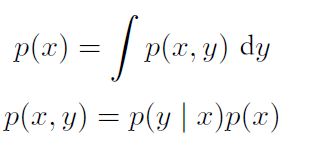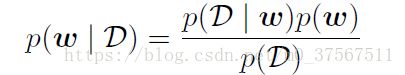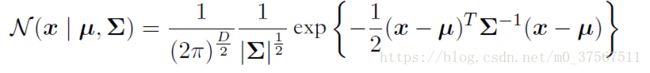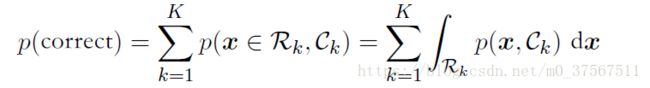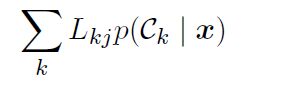PRML读书笔记（第一章）

2018/4/2:

1.对于最简单的损失函数：

该误差函数是系数w的二次函数，因此它关于w的偏导数是线性函数，所以误差函数的最小值有一个唯一解；

2.均方根误差（RMS）公式：

3.随着M的增大（M为模型多项式的阶），模型的系数也越来越大，这样是可以让多项式函数精确的与数据匹配，但是与此同时，对于数据之间的点，多项式的值会表现出剧烈的震荡，有着更大的M值的更灵活的多项式被过分地调参，使得多项式被调节成了与目标值的随机噪声相符，我想起正则项L2减小过拟合的策略好像就是使权值尽量小一些，大概原因也是出于这里吧，本章后续关于正则化的实验也表明了当系数越小时，模型会越简单；

4.在给定条件下，也就是形如p(B|A=1)，那么A = 1下B所有可能取值的概率和为1；

5.先验概率：事件发生前已知的经验概率

    后验概率：事件发生后由结果和先验概率以及贝叶斯定理推导出来的对经验概率的修正概率（都是我自己YY出来的概念，差不多就是这个意思）；

P20;

2018/4/3:

1.联合概率密度与单个概率密度的关系：

2.协方差定义：

它度量了多大程度上x,y会共同变化，若x,y相互独立，则它们的协方差为0；在两个随机向量x和y的情形下，协方差是一个矩阵：

3.贝叶斯定理的形式为：

贝叶斯定理右侧的p(D|w)由观测数据集D（也就是那个盒子和水果实验中对指定的盒子，抓到指定水果的频率）来估计，可以被看成参数向量w的函数，被称为似然函数（likelihood function）；

4.D维向量的高斯分布：

5.最大似然方法法系统化地低估了分布的方差。这是一种叫做偏移（bias）的现象的例子，与多项式曲线拟合问题中遇到的过拟合问题相关，根源是方差的最大似然估计不是无偏估计，它是无偏估计的(N-1)/N(回忆数理统计知识);

6.当数据点的数量N增大时，最大似然解的偏移会变得不太严重， 并且在极限N趋近于无穷大的情况下，⽅差的最⼤似然解与产⽣数据的分布的真实方差相等。在实际应用中，只要N的值不太小，那么偏移的现象不是个大问题。然而，在本书中，我们感兴趣的是带有很多参数的复杂模型。这些模型中，最大似然的偏移问题会更加严重。实际上，我们会看到，最大似然的偏移问题是我们在多项式曲线拟合问题中遇到的过拟合问题的核心。

7. 1.2.5最后的最大后验概率有点没看懂；

8.控制模型参数分布的参数，被称为超参数，比如卷积核大小，控制了卷积核有多少个参数，它就是超参数，而像学习率就不是超参数；

P30

2018/4/4（决策论以及决策与推断的结合）

1.在高维空间中，一个球体的大部分体积都聚集在表面附件的薄球壳上（这个其实就可以理解为越高维空间的球，体积对半径的导数也是越高阶的）；

2.最大化正确率：

对于处于Rk的x,选择使p(x,Ck)最大的Ck，这样求出来的积分是最大的；

3.损失矩阵，对于某个新的输入向量x，其真实类别为k，分类类别为j，可以看成损失矩阵的第k,j个元素，我们可以根据实际情况和需求，加大某些错分情况的损失函数值，书中所举的例子是预测癌症，将癌症病人预测为健康的后果比将健康者预测为患癌症的后果要严重得多，所以应增大这种错分情况的损失；

4.最小化期望损失的决策规则是对于每个新的样本x,把它分到能使下式取得最小值的第j类：

5.拒绝选项：对于最大预测概率小于设定的阈值的样本，不对其进行预测；

6.有监督机器学习方法可以分为生成方法和判别方法（常见的生成方法有混合高斯模型、朴素贝叶斯法和隐形马尔科夫模型等，常见的判别方法有SVM、LR等），生成方法学习出的是生成模型，判别方法学习出的是判别模型。

判别式模型，就是只有一个模型，你把测试用例往里面一丢，label就出来了，如SVM。生成式模型，有多个模型(一般有多少类就有多少个)，你得把测试用例分别丢到各个模型里面，最后比较其结果，选择最优的作为label，如朴素贝叶斯。

简单理解：生成模型，对输入向量和label计算联合分布，能够体现数据的分布信息；判别模型，计算条件概率分布；

7. 1.5.5 回归问题的损失函数公式推导没看懂。。。

P40

2018/4/8

1.信息增益(信息熵)的计算：

信息增益函数h(x)的形式可以这样寻找：如果我们有两个不相关的事件x和y，那么我们观察到两个事件同时发⽣时获得的信息应该等于观察到事件各自发生时获得的信息之和，即h(x, y) = h(x) + h(y)。两个不相关事件是统计独立的，因此p(x, y) = p(x)p(y)。根据这两个关系，很容易看出h(x)一定与p(x)的对数有关。因此有：

，

负号确保了信息量一定是非负数，大概率事件对应于高的信息量，那么对于一个随机变量x，它的信息量的期望就是：

使用2为底数的对数函数，信息量的单位是bit;

2.概率计算中乘积的关系，到了信息量计算中就是加和的关系，如：

，

其中，H[x, y]是p(x, y)的微分熵，H[x]是边缘分布p(x)的微分熵。因此，描述x和y所需的信息是描述x自己所需的信息，加上给定x的情况下具体化y所需的额外信息。

3.互信息。互信息与条件熵之间的关系为：

我们可以把互信息看成由于知道y值而造成的x的不确定性的减小（反之亦然）。从贝叶斯的观点来看，我们可以把p(x)看成x的先验概率分布，把p(x|y)看成我们观察到新数据y之后的后验概率分布。因此互信息表示一个新的观测y造成的x的不确定性的减小。

P50