音频噪声抑制(3):维纳(Wiener)滤波器篇之有辅助观测数据
前面的文章讲了,维纳滤波器的设计和用维纳滤波器来抑制噪声。
Review:维纳滤波器的设计
Review:噪声抑制之维纳(Wiener)滤波器篇
当时的噪声抑制,有两个阶段。滤波器系数的求解阶段,和后面的噪声抑制阶段。
可能这样能有一丢丢效果,但好像并不是很理想。
对音频信号噪声抑制的提升一种手段就是,多花点钱,用两个麦克风。一个录语音(含噪v2),另一个录噪声(v1)。v2和v1可能不同,但两者之间却存在一定的关系。
据说,飞机上就是这样的设计。
坐过飞机的人应该都有这样的体会,飞机那个引擎声,真的是震耳欲聋的。尤其是助跑加速起飞前的那一瞬间!
这么大的噪声,这么恶劣的环境,这么低的信噪比,如果塔台和飞行员要通话,不进行噪声抑制,根本没法正常通信啊!
不可能用44100kHz采样、24bit量化、双声道传输吧…
一开始,麦克风接收飞行员的声音在量化的时候已经有量化噪声了。
再加上这么大的引擎噪声。必须去噪啊!
所以,有些天才就这么设计语音系统了。
基本思想大概是这样。
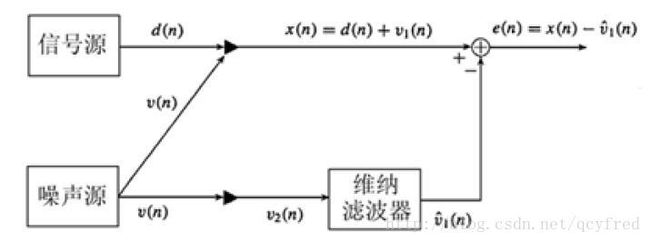
假设飞行员说话的信号时x(t),发动机的噪声时v1(t),v1(t)传到麦克风这里,由于经过了某个信道,变成了v2(t),
叠加到纯净的语音信号x(t)上,麦克风收到的就是y(t) = x(t) + v2(t)了。
所以,如果能在发动机附近也装一个麦克风,去收集来自发动机的噪声v1(t),再通过一些技术手段,利用v1(t)估计出v2(t),
再用y(t) - v2(t)的估计,就应该能得到比较纯净的语音信号x(t)了吧。
这就是,有数据辅助的维纳噪声抑制。
下面是我上学期一门课的一次作业,讲的就是这个案例。
% 2016年5月17日计算机作业
% 作者:qcy
clear;
close all;
clc
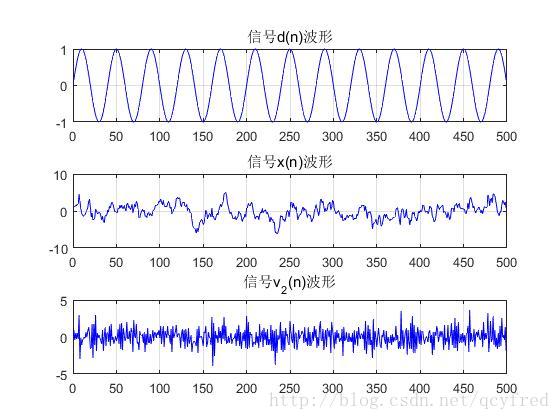
%% (a)问 画波形
% rand('seed',1);
% randn('seed',1);
N = 500; % 样点个数
n = (0:N-1)';
phi = 0; % 正弦信号初相角
omega_0 = 0.05 * pi;
g_noise = randn(N,1);
d = sin(n*omega_0 + phi);
A1 = [1 -0.8]; % v1的系数A
B1 = 1; % v1的系数B
A2 = [1 0.6]; % v1的系数A
B2 = 1; % v2的系数B
v1 = filter(B1,A1,g_noise);
v2 = filter(B2,A2,g_noise);
x = d + v1;
figure(1);
subplot(311);
plot(n,d,'b');
grid on;
title('信号d(n)波形');
subplot(312);
plot(n,x,'b');
grid on;
title('信号x(n)波形');
subplot(313);
plot(n,v2,'b');
grid on;
title('信号v_2(n)波形');
%% (b)问 根据v2,通过估计的w后,估计v1,含噪信号 x - v1_est --> 去噪信号
p1 = 3;
p2 = 6;
p3 = 9;
p4 = 12;
% 阶数是 p 的话,滤波器的系数有 p+1 个
% 由v2估计v1,可以得到的 Wiener-Hopf方程为 Rv2 * w = Rxv2
% 求Rv2
rv2 = xcorr(v2,'unbiased'); % 由x计算自相关函数算出来的
figure(2);
plot(rv2)
rv2_non_neg = rv2(N:end); % 下标从零开始的自相关序列
% 求rxv2
rxv2 = xcorr(x,v2,'unbiased');
rxv2_non_neg = rxv2(N:end);
% 1. p=3, 矩阵阶数4
r_p1 = rv2_non_neg(1:p1+1).';
R_p1 = toeplitz(r_p1);
Rxv2_p1 = rxv2_non_neg(1:p1+1);
w1 = R_p1\Rxv2_p1;
% 维纳滤波
v1_est_p1 = filter(w1,1,v2);
delta_v1_p1 = v1_est_p1 - v1;
error2_p1 = mean(delta_v1_p1.^2);
% 去噪
d1_est = x - v1_est_p1;
% 2. p=6,矩阵阶数10
r_p2 = rv2_non_neg(1:p2+1).';
R_p2 = toeplitz(r_p2);
Rxv2_p2 = rxv2_non_neg(1:p2+1);
w2 = R_p2\Rxv2_p2;
% 维纳滤波
v1_est_p2 = filter(w2,1,v2);
delta_v1_p2 = v1_est_p2 - v1;
error2_p2 = mean(delta_v1_p2.^2);
% 去噪
d2_est = x - v1_est_p2;
% 3. p=9
r_p3 = rv2_non_neg(1:p3+1).';
R_p3 = toeplitz(r_p3);
Rxv2_p3 = rxv2_non_neg(1:p3+1);
w3 = R_p3\Rxv2_p3;
% 维纳滤波
v1_est_p3 = filter(w3,1,v2);
delta_v1_p3 = v1_est_p3 - v1;
error2_p3 = mean(delta_v1_p3.^2);
% 去噪
d3_est = x - v1_est_p3;
% 4. p=12
r_p4 = rv2_non_neg(1:p4+1).';
R_p4 = toeplitz(r_p4);
Rxv2_p4 = rxv2_non_neg(1:p4+1);
w4 = R_p4\Rxv2_p4;
% 维纳滤波
v1_est_p4 = filter(w4,1,v2);
delta_v1_p4 = v1_est_p4 - v1;
error2_p4 = mean(delta_v1_p4.^2);
% 去噪
d4_est = x - v1_est_p4;
% 均方误差
error2 = [error2_p1;error2_p2;error2_p3;error2_p4];
p_index = [p1 ;p2 ;p3 ;p4];
figure(2);
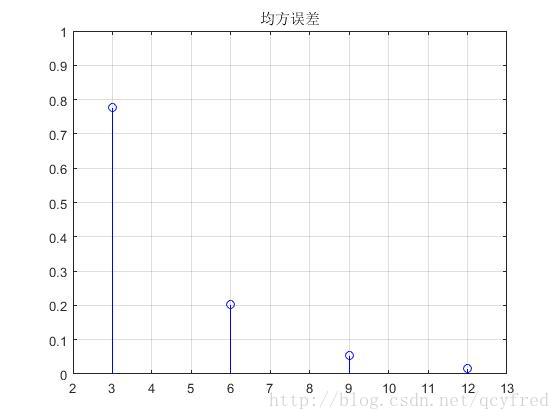
stem(p_index,error2,'b');
grid on;
title('均方误差');
axis([2 13 0 1]);
figure(3);
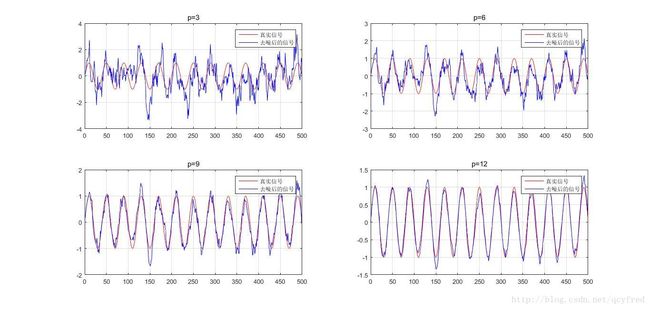
subplot(221);
plot(n,d,'r');hold on;
plot(n,d1_est,'b');
grid on;
title('p=3');
legend('真实信号','去噪后的信号');
subplot(222);
plot(n,d,'r');hold on;
plot(n,d2_est,'b');
grid on;
title('p=6');
legend('真实信号','去噪后的信号');
subplot(223);
plot(n,d,'r');hold on;
plot(n,d3_est,'b');
grid on;
title('p=9');
legend('真实信号','去噪后的信号');
subplot(224);
plot(n,d,'r');hold on;
plot(n,d4_est,'b');
grid on;
title('p=12');
legend('真实信号','去噪后的信号');
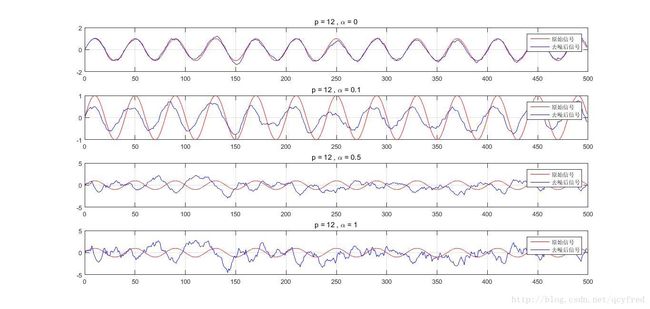
%% (c) 所观察的辅助数据中,泄露原始信号,对噪声抑制的影响
alphas = [0 0.1 0.5 1];
for k = 1:length(alphas)
alpha = alphas(k);
v0 = v2 + alpha * d;
% 由v0估计v1,可以得到的 Wiener-Hopf方程为 Rv0 * w = Rxv0
% 求Rv0
rv0 = xcorr(v0,'unbiased'); % 由x计算自相关函数算出来的
rv0_non_neg = rv0(N:end); % 下标从零开始的自相关序列
% 求rxv0
rxv0 = xcorr(x,v0,'unbiased');
rxv0_non_neg = rxv0(N:end);
% 1. p=12, 矩阵阶数13
rv0_p4 = rv0_non_neg(1:p4+1).';
Rv0_p4 = toeplitz(rv0_p4);
Rxv2_p4 = rxv0_non_neg(1:p4+1);
w = Rv0_p4\Rxv2_p4;
% 维纳滤波
v1_est_p4 = filter(w,1,v0);
% 去噪
d1_est = x - v1_est_p4;
figure(4);
subplot(length(alphas)*100 +10+ k);
plot(n,d,'r');
hold on;
grid on;
plot(n,d1_est,'b');
legend('原始信号','去噪后信号');
title(['p = 12 , \alpha = ' num2str(alpha)]);
end
但是,滤波器阶数太高了,似乎噪声抑制的效果反而变差了!
这是为什么呢?在课堂上,我们的讨论结果是,可能因为取的x的样本点数目有限,阶数太高,自相关函数估计就不准了…
滤波后的结果如下。
如果辅助观测信号也泄露了一些“所期望”的信号以后,效果也会变差的。
最后,这种噪声抑制效果的提升,还是付出了很大的代价的。至少有两点,
第一,要多买一个麦克风。
第二,还要有机会能采集到“基本干净”的噪声。