Guided Anchoring 论文笔记
前言
作者提出设计anchor时的两个准则:
- aligment——使用卷积特征作为anchor的表示特征,anchor的中心要与特征图中的像素对齐;
- consistency——在特征图的不同位置,感受野的大小是一致的,因此不同位置anchor的尺度和形状也要保持一致。
本文希望得到的是稀疏的、根据位置可变的anchor。作者观察到,图像中的目标并不是均匀分布的,目标的尺度与图像的内容、场景的位置及几何形状密切相关。由此作者提出生成稀疏的anchor的步骤:
- 首先确定可能包含目标的子区域;
- 然后确定不同位置anchor的形状。
这种方式可以让anchor自己学习形状的设计,但是这违背了之前提到的consistency这一准则。anchor的尺度和长宽比现在是可变的,那么不同的特征图的像素要根据相对应的anchor学习调整特征表示。本文设计了feature adaption模块来修正特征图使之与 anchor 形状更加匹配。
本文做出的贡献:
- 本文提出了新的anchor机制,可以预测稀疏的、任意形状的anchor;
- 将anchor的联合分布分解为两个条件分布,并分别使用模型进行建模;
- 设计feature adaption模块来修正特征图使之与 anchor 形状更加匹配;
- 研究了two-stage检测器高质量的proposal,并提出一种提高已训练的模型的性能。
Guided Anchoring
一个anchor的形状和位置可以由 ( x , y , w , h ) (x,y,w,h) (x,y,w,h)来表示,其中 ( x , y ) (x,y) (x,y)是anchor中心点的坐标, w w w和 h h h分别是宽和高。给定一个输入图像 I I I,anchor的分布可以被分解为两个条件分布:
![]()
anchor的概率分布被分解为两个条件概率分布,也就是给定图像特征之后anchor中心点的分布,和给定图像特征和中心点之后anchor形状的概率分布。根据这个公式,anchor的预测可以被分为两个步骤,anchor位置预测和形状预测。anchor生成模型的结构如下:
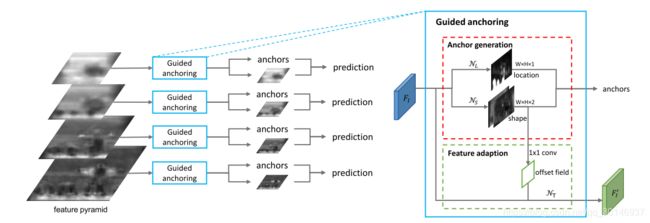
图中红色虚线框内的部分就是anchor生成模型,它包括位置预测分支和形状预测分支。给定一个输入图像 I I I,首先得到特征图 F I F_{I} FI,位置预测分支在 F I F_{I} FI上生成一个概率map,说明目标可能会出现的位置;形状预测分支在这些位置上预测最有可能出现的形状。后来结合两个分支的输出结果,通过比较预测的概率值超过一定阈值来得到一些可能的位置,然后在这些位置上结合最有可能的形状来生成一系列anchor。之后采用feature adaption模块,根据anchor的形状来对特征进行调整,得到新的特征图 F I ′ F^{'}_{I} FI′供之后的预测(anchor 的分类和回归)使用。
anchor生成模型结合了FPN,在多层级的特征图上进行anchor的生成。同时,anchor生成的参数在所有层级之间都是共享的,因此效率较高。
1. anchor位置的预测
位置预测分支生成一个和输入特征图 F I F_{I} FI大小相同的概率map p ( ⋅ ∣ F I ) p(·|F_{I}) p(⋅∣FI),在概率map上的概率值 p ( i , j ∣ F I ) p(i,j|F_{I}) p(i,j∣FI)与原始输入图像 I I I上的点 ( ( i + 1 / 2 ) s , ( j + 1 / 2 ) s ) ((i+1/2)s,(j+1/2)s) ((i+1/2)s,(j+1/2)s)相对应,其中 s s s是特征图的步长。这个概率值说明了目标中心在这个位置上存在的可能性的大小。
p ( i , j ∣ F I ) p(i,j|F_{I}) p(i,j∣FI)由子网 N L N_{L} NL产生,这个子网在 F I F_{I} FI上采用1 × 1的卷积得到objectness score的map,然后通过一个element-wise的sigmoid函数转换为概率值。虽然一个更深的子网可以得到更精确的预测结果,但这种方法可以使速度和精度之间达到平衡。
基于概率map p ( ⋅ ∣ F I ) p(·|F_{I}) p(⋅∣FI),如果一些概率值超过了阈值 ϵ L \epsilon_{L} ϵL,那么就选择这些概率值对应的位置作为目标中心可能存在的位置。这一步可以在保持召回率的条件下过滤掉90%的区域。在inference时,用masked conv替代普通的conv,以提高速度。
2. anchor形状的预测
在确定了目标可能会出现的位置后,接下来就是判断相应位置anchor可能的形状。形状预测分支与边界框回归是不同的,它没有改变anchor的位置,因此不会造成anchor与特征图之间不匹配的问题。给定一个特征图 F I F_{I} FI,这个分支会在每个位置上预测出一个最佳形状 ( w , h ) (w,h) (w,h),预测出的形状可能会与最近的gt产生较高的IoU。但是由于 w w w和 h h h的范围太大了,直接预测的话会非常不稳定。因此采用如下的转换:
![]()
形状预测分支输出的就是 d w dw dw和 d h dh dh,然后通过上式映射到 ( w , h ) (w,h) (w,h),其中 s s s是步长, σ \sigma σ是缩放因子,在这里 σ = 8 \sigma=8 σ=8。该非线性转换将输出的空间从[0,1000]映射到[-1,1],得到稳定的学习目标 。该分支通过一个1 × 1 × 2的子网 N S N_{S} NS进行预测,得到 d w dw dw和 d h dh dh,然后通过上式进行转换。
通过该方法,一个位置只预测一个形状动态变化的anchor,实验证明,由于位置和形状之间的密切联系,guided anchoring具有更高的召回率,并且能更好的捕捉具有极端大小目标的信息。
3. feature adaption
在RPN或者一些single-stage检测器中,每个位置上anchor的尺度和形状都是相同的,因此特征图的表示是一致的。而在本文的机制中,每个位置上anchor的形状各有不同,和特征不能特别好的匹配;另外,因为接下来的分类和回归是基于预测出的anchor来做的,但特征图并不知道形状预测分支预测的anchor的形状,因此不能继续像以前一样用一个全卷积分类器作用在特征图上。
本文提出feature adaption模块,基于每个位置的anchor形状来调整特征的形状,就是把 anchor 的形状信息直接融入到特征图中,这样新得到的特征图就可以去适应每个位置 anchor 的形状:
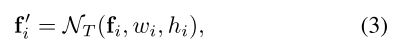
其中 f i f_{i} fi是第 i i i个位置的特征, ( w i , h i ) (w_{i},h_{i}) (wi,hi)是该位置上对应的anchor的形状。
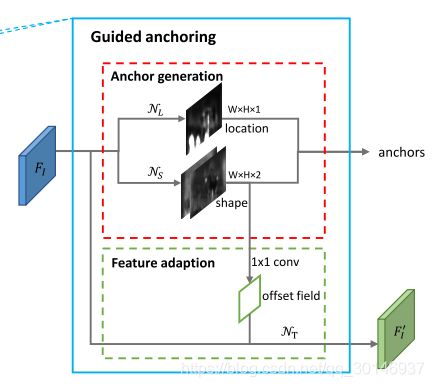
为了实现这个变换,采用了一个3 × 3 的可变卷积层(deformable convolutional) N T N_{T} NT,如上图所示。首先根据形状预测分支的输出预测一个offset field,然后将原始的特征图 F I F_{I} FI通过 N T N_{T} NT并结合offset field得到 F I ′ F^{'}_{I} FI′,最后在 F I ′ F^{'}_{I} FI′上进行分类与回归。注意,可变卷积的offset field是通过anchor的w和h经过一个1×1的卷积得到的。
Training
1. 损失函数
训练是端到端的,使用的是多任务损失函数。除了分类损失 L c l s L_{cls} Lcls和回归损失 L r e g L_{reg} Lreg之外,还引入了另外两个loss,分别是anchor定位损失 L l o c L_{loc} Lloc和anchor形状预测损失 L s h a p e L_{shape} Lshape。总loss为:
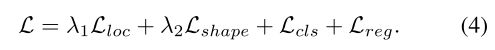
2. anchor的定位
为了训练anchor定位分支,每个图像需要一个binary lable map,其中1表示可以把一个anchor放到这个位置上,0则相反。首先,将gt box ( x g , y g , w g , h g ) (x_{g},y_{g},w_{g},h_{g}) (xg,yg,wg,hg)映射到对应的特征图上的尺度为 ( x g ′ , y g ′ , w g ′ , h g ′ ) (x^{'}_{g},y^{'}_{g},w^{'}_{g},h^{'}_{g}) (xg′,yg′,wg′,hg′),设 R ( x , y , w , h ) R(x,y,w,h) R(x,y,w,h)表示一个矩形区域,其中 ( x , y ) (x,y) (x,y)是中心点, w w w和 h h h分别是宽和高。anchor越接近gt box的中心越好,这样可以得到较大的IoU,因此为每个gt box设计了如下三种区域:

- 中心区域 C R = R ( x g ′ , y g ′ , σ 1 w ′ , σ 1 h ′ ) CR=R(x_{g}^{'},y_{g}^{'},\sigma_{1}w^{'},\sigma_{1}h^{'}) CR=R(xg′,yg′,σ1w′,σ1h′),也就是gt box靠近中心部分的区域,如图中的绿色区域。在 C R CR CR中的像素都是正样本;
- 忽略区域 I R = R ( x g ′ , y g ′ , σ 2 w ′ , σ 2 h ′ ) IR=R(x_{g}^{'},y_{g}^{'},\sigma_{2}w^{'},\sigma_{2}h^{'}) IR=R(xg′,yg′,σ2w′,σ2h′)\ C R CR CR,其中 σ 2 > σ 1 \sigma_{2}>\sigma_{1} σ2>σ1。 I R IR IR比 C R CR CR大,但不包含 C R CR CR,如图中的黄色区域。 I R IR IR中的像素在训练时是被忽略的;
- 外部区域 O R OR OR,就是特征图除 I R IR IR和 C R CR CR之外的部分,如图中的灰色区域。 O R OR OR中的像素都是负样本。
guided anchoring框架使用的FPN,也就是有多尺度的特征图,因此每个层级的特征图上都是需要预测anchor的位置的。每个层级的特征图只能负责预测特定尺度范围的目标,因此还要考虑邻近的特征图的影响。具体来说就是,如果一个目标的尺度落入某个层级特征图所负责的尺度范围,就把gt box映射到这个特征图上,把 C R CR CR也分配到这个特征图上;在与这个特征图相邻的特征图上,将相同区域设为 I R IR IR,如上图所示。当某个层级上有多个目标重叠时, C R CR CR可以抑制 I R IR IR, I R IR IR可以抑制 O R OR OR。
由于 C R CR CR只负责整个特征图上的一小部分,因此用focal loss来训练定位分支。
3. anchor的形状
确定anchor的最佳形状需要两个步骤:
- 将anchor与gt box匹配;
- 预测anchor的宽和高,使其能更好的覆盖匹配的gt box。
按照之前的做法,通过计算anchor与所有gt box之间的IoU,然后将anchor分配给IoU最大的那个gt box。但是这种方法并不适用于现在的anchor,因为现在的anchor的 w w w和 h h h是不确定的,是需要预测的变量。为了解决这个问题,重新定义IoU,将anchor a w h = a_{wh}= awh={ ( x 0 , y 0 , w , h ) ∣ w > 0 , h > 0 (x_{0},y_{0},w,h)|w>0,h>0 (x0,y0,w,h)∣w>0,h>0} 与gt box g t = ( x g , y g , w g , h g ) gt=(x_{g},y_{g},w_{g},h_{g}) gt=(xg,yg,wg,hg)之间的IoU表示为:
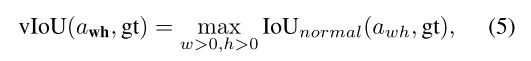
其中 I o U n o r m a l IoU_{normal} IoUnormal是经典的IoU定义, w w w和 h h h是变量。对于任意一个anchor与gt,计算它们之间的vIoU是很复杂的,也不可能把 w w w和 h h h遍历一遍求最大值,因此采用了近似的方法。对于一个给定的anchor ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0),采样一些 w w w和 h h h的可能值,然后计算这些采样的anchor与gt之间的IoU,取最大值作为vIoU的近似。理论上,采样的组数越多,近似的效果越好,但出于效率的考虑,训练时共采样了9组 ( w , h ) (w,h) (w,h)。作者通过实验发现,最终结果对采样的组数这个超参并不敏感,也就是说不管采样多少组,近似效果已经足够。
形状预测分支的损失函数是bounded iou loss的变体:
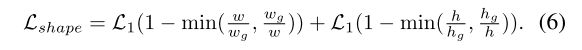
其中 ( w , h ) (w,h) (w,h)是预测的anchor的形状, ( w g , h g ) (w_{g},h_{g}) (wg,hg)是它对应的gt box的形状。 L 1 L_{1} L1是smooth L1 loss。
高质量的proposal
GA-RPN(由guided anchoring强化过的RPN)可以生成质量更高的proposal,本文研究如何利用这些高质量的proposal来提升two-stage检测器的性能。
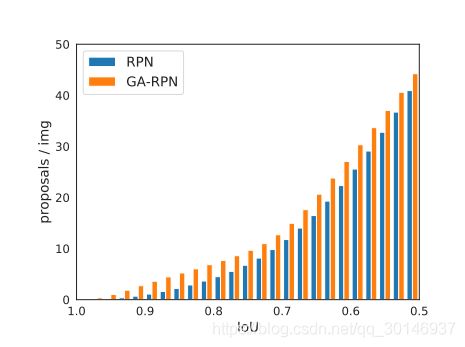
上图展示了RPN和GA-RPN生成的proposal的IoU分布,可以看到GA-RPN有两个明显的优点:
- 正样本更多;
- 高IoU的proposal比例更显著;
那么自然而然地就会产生这样一个想法:用GA-RPN代替现有模型中的RPN,然后进行端到端的训练。但是实验证明,这种做法带来的效果的提升比较有限。通过观察发现,使用高质量proposal的先决条件是根据proposal的分布进一步调整训练样本的分布。因此,相比RPN,训练GA-RPN时改进的地方有两点:
- 减少proposal的数量;
- 增大练时正样本的 IoU 阈值(这个更重要)。既然在top300里面已经有了很多高IoU的proposal,那么何必用1000个框来训练和测试,既然proposal们都这么优秀,那么让IoU标准严格一些也未尝不可。
参考
作者自己写的论文解读