每日算法——最长连续序列,合并链表,合并k个链表等
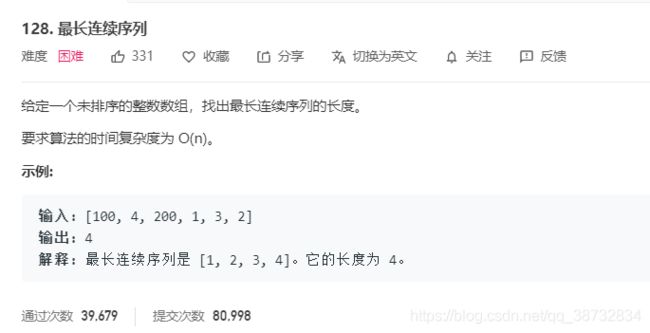
啊啊啊这道题我居然做过,我一点印象都没有了。
先来看一下目标,找连续的序列,连续的意味着 最小值+长度-1 = 最大值,且中间值相差为1.
这题有三种思路或者说两种。
1.动态规划:
像这种最长序列啊,子串啊,之类的第一反应就是动态规划啦
比较常规,比起暴力多了一个判断,只有当它前一个值不存在时才重看(因为这是可能的最长开始),一直查找到它的最长的情况,然后换下一个数,
这种算法表面上是O(n^2),其实是O(n),添加到set中,n次,
然后之后只有可能只会在出现新的可能的开始点时,才会执行操作,对应的操作就是n次,也就是说总共2n次。
这种操作我感觉还是有点动态规划的思想:
如果常规的数组定义:
dp[i][j] = 第i个数以前,遍历到j为止的长度情况
不过因为是连续的,所以不会出现覆盖这些情况,可以优化为dp[i]
2.转移方程:
dp[i] = if dp[i-1]==0? (j=i+1)while(dp[j++] != 0) {dp[i]++}
3.初始化
将能够命中的值初始化为1
dp[nums] = 1;
不过这种做法很麻烦(比如负数的情况,需要0偏移最小负数的绝对值),而且去重得自己手动加判断不重复判断
这里实现了>=0的版本
class Solution {
public int longestConsecutive(int[] nums) {
if(nums.length<=1){
return nums.length;
}
int[] dp = new int[Arrays.stream(nums).max().getAsInt()+2];
IntStream.of(nums).boxed().forEach(i->dp[i] = 1);
int ans = 0;
for(int i:nums){
if((i==0||dp[i-1]==0)&&dp[i]!=1){
int j = i+1;
while(dp[j]!=0){
dp[i]++;
j++;
}
ans = Math.max(dp[i],ans);
}
}
return ans;
}
}
所以还是用set来存储吧
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
IntStream.of(nums).boxed().forEach(set::add);
int ans = 0;
for(int i:set){
int count =1;
if(!set.contains(i-1))
while(set.contains(i+1)){
i++;
count++;
}
ans = Math.max(ans,count);
}
return ans;
}
}
还有一种思路,
dp[i]的状态定义为dp[i] = i数左右相邻的连续数字之和最大为多少。
转移方程:
dp[i] = dp[i+1]+dp[i-1]+1
同时需要更新当前的边界值
dp[i-dp[i-1]] = dp[i];
dp[i+dp[i+1]]=dp[i];
初始化:无
不过由于刚才所说的负数等情况,所以使用了HashMap。
class Solution {
public int longestConsecutive(int[] nums) {
Map<Integer,Integer> map = new HashMap<>();
int ans = 0;
for(int i:nums){
if(!map.containsKey(i)){
int left = map.getOrDefault(i-1,0);
int right = map.getOrDefault(i+1,0);
map.put(i,left+right+1);
map.put(i-left,left+right+1);
map.put(i+right,left+right+1);
}
ans = Math.max(ans,map.get(i));
}
return ans;
}
}
还有一种思路就是使用并查集,这个数据结构有点意思,一个数组或者map也好的结构,不过一个元素的value会是另一个元素的key。在这道题里面,我那个按顺序的序列正好就可以满足并查集的结构(可以想象成上是相互连接的图)。
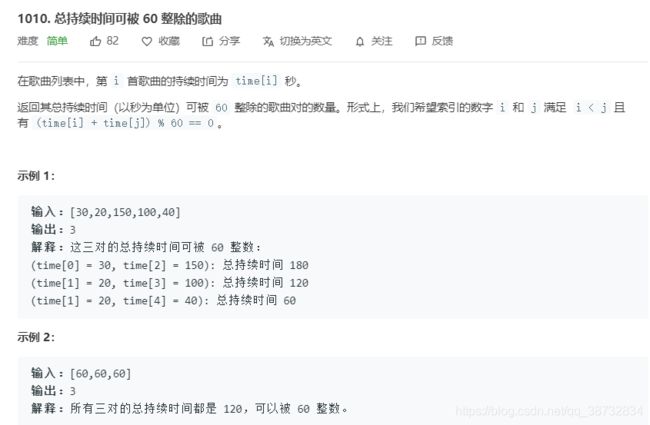
首先将值转换为60的余数,且满足两两之和为60,由于每首歌都是不一样的,所以假设余数i+j=60,则size(i)*size(j) = 对数,而相同时间的比如0和0,30和30,则为(size(i)*size(i-1))/2
class Solution {
public int numPairsDivisibleBy60(int[] time) {
int[] r = new int[60];
IntStream.of(time).forEach(i->r[i%60]++);
int ans = (r[0]*(r[0]-1))>>1;
for(int i=1;i<30;i++){
int min = r[i]*r[60-i];
ans+=min;
}
ans += (r[30]*(r[30]-1))>>1;
return ans;
}
}
俺又看到一种聪明的算法:
这样少一了一次遍历30,机智机智。
class Solution {
public int numPairsDivisibleBy60(int[] time) {
int[] dp = new int[60];
int res = 0;
for(int num : time){
num %= 60;
res += dp[num == 0 ? 0 : 60 - num];
dp[num]++;
}
return res;
}
}
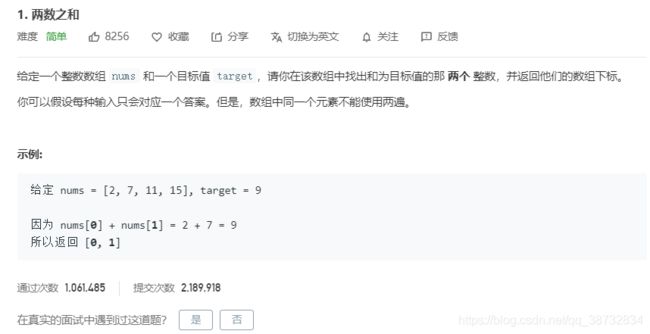
这道题好像是第一题?
遍历数组,就用个HashMap存一下原值即可(值为索引),如果发现新的值的差值在HashMap中已经存在过了,则返回当前索引和HashMap中对应的值
class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap<Integer,Integer> map= new HashMap<>();
for(int i =0;i<nums.length;i++){
int temp = target-nums[i];
if(map.containsKey(temp))
return new int[]{map.get(temp),i};
map.put(nums[i],i);
}
throw new IllegalArgumentException("没得没得");
}
}
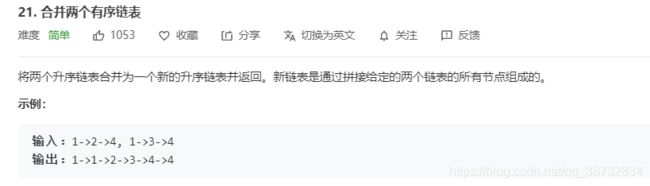
这个就是归并排序的治的过程,不过数组变成了链表而已,从自顶向下的思路,假设A链表长度为a,B:b,则a+b=最后的长度,那么哪个节点应该在哪个位置呢?首先是排好序的,再次合并的时候,只需要将两者比较小的那个留在本位置就行了,然后小的那个指针后移,重复之前操作,直到某个链表为空。
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1==null){
return l2;
}
if(l2==null){
return l1;
}
if(l1.val<l2.val){
l1.next = mergeTwoLists(l1.next,l2);
return l1;
}else{
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
}
}
上一题的升级版,不过现在是归并排序的并的完整过程。
同样用递归自顶向下的方式,从索引最右边开始合并,两两合并,然后等待当前的mid以左两两合并,然后再等待mid以左同样的过程,最后合并为一条链
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists == null || lists.length == 0) return null;
return merge(lists.length-1,0,lists);
}
private ListNode merge(int right,int left,ListNode[] lists){
if(left>=right){
return lists[left];
}
int mid = (left+right)>>1;
ListNode leftL = merge(right,mid+1,lists);
ListNode rightL = merge(mid,left,lists);
return merge(rightL,leftL);
}
private ListNode merge(ListNode node1, ListNode node2) {
if(node1==null)
return node2;
if(node2==null)
return node1;
if(node1.val<node2.val){
node1.next = merge(node1.next,node2);
return node1;
}else{
node2.next = merge(node1,node2.next);
return node2;
}
}
}
这是一道数学题,求x2最接近a的x,比较暴力的方式就是到2~a/2之前逐一查找,不过这个是有顺序的,可使用二分查找法。
class Solution {
public int mySqrt(int a) {
if(a<=1)
return a;
long left = 1,right = a>>1;
while(left<right){
long mid = (left+right+1)>>1;
if(mid*mid==a){
return (int)mid;
}
if(mid*mid>a){
right = mid-1;
}else{
left = mid;
}
}
return (int)left;
}
}
class Solution {
public int mySqrt(int a) {
long x = a;
while (x * x > a) {
x = (x + a / x) / 2;
}
return (int) x;
}
}
