目标检测 | Anchor free之CornerNet网络深度解析
点击上方“AI算法修炼营”，选择“星标”公众号
精选作品，第一时间送达
1 前言
最近又跳回来继续学习基于anchor free的目标检测模型，具体包括CornerNet和CenterNet等网络结构 。
学习anchor free的detector目的如下：
（1） 作为以目标检测领域入门深度学习的小白，如果目标检测领域没有接触到anchor free，显得我很业余，很不专业（当然，这仅仅是心理作用罢了哈哈）
（2） 接触一些目标追踪领域的文章，遇到了如下的一些关键字：Objects as points、anchor-free等，这不为了学习MOT打一下基础嘛
图1 一对点进行bounding box位置预测
所以本文就我在CornerNet论文解读和代码解析过程中的一些见解，以文字的形式进行总结。
论文和代码链接如下：
paper：https://arxiv.org/abs/1808.01244
code : https://github.com/princeton-vl/CornerNet
我在学习一种新的模型/网络时，喜欢按照下面步骤进行探索。
（1） 在知乎/CSDN上找相关的（解析）博客，进行初步印象的建立
（2） 细读原文paper
（3） 开始跑代码，看代码，深入理解
可是我在知乎上看了一大堆关于cornerNet的文章，总觉得千篇一律（虽然大家写的很认真），但是感觉就是对原文的翻译，少了一些个人的理解在里面。
2 Corner Net的一些基础知识
所以本次我想对cornerNet进行更深度的解析，便于以后的我和各位读者更好的理解。
论文的名字是这样的，CornerNet: Detecting Objects as Paired Keypoints。那么CornerNet 是根据一对关键点来进行物体的检测的。
该论文的主要创新为
（1） anchor-free 的目标检测新思路
（2） corner pooling的提出
（3） cornerNet网络的提出
那么不妨会出现以下几个疑问：
（1）问题1，具体是哪一对关键点呢？
原文中提到
We propose CornerNet, a new approach to object detection where we detect an object bounding box as a pair of keypoints, the** top-left corner** and the bottom-right corner, using a single convolution neural network.
作者的意思就是我们只需要预测物体包围框的左上点坐标（top-left corner）和右下角坐标(bottom-right corner)，那么就可以完成对物体的检测了。就像上图1一样。
那么原来需要设置很多anchor进行 region proposal的方法变成了一对对关键点的检测了。
我们都知道，anchor-based的方法，虽然目前有的方法可以满足实时性要求（如YOLO、SSD等），但是仍然会消耗大量的时间在anchor的计算上。所以作者另辟思路，提出了anchor-free的cornerNet这种方法，提高了检测的速度和精度。
（2）问题2：如何匹配同一物体bounding box的左上角和右下角？
原文中提到
The network also predicts an embedding vector for each detected corner [27] such that the distance between the embeddings of two corners from the same object is small.
也就是cornerNet在进行预测的时候，会为每个点分配一个embedding vector，属于同一物体的点的vector的距离较小。如下图2所示。
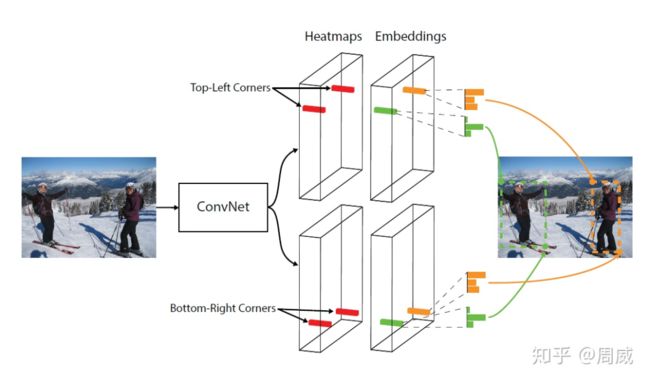图2 corner的embedding
（3） 问题3：什么是corner pooling ? 干什么的？有什么用？
我们知道max pooling，知道average pooling，但是没有见过corner pooling。本文将提出了一种适用于cornerNet网络的corner pooling，目的是为了建立点corner和目标的位置关系。
一般而言，知道了bounding box的左上角和bounding box的右下角就可以确定位置所在的范围和区域。
那么我们从bounding box左上角(top-left corner)看物体。视线横着的话，物体就在视线的下面（那么视线所在位置为the topmost boundary of an object）。视线竖着的话，物体就在视线的右边，那么视线位置为the leftmost boundary。如下图3所示。
图3
那么 top-left corner pooling 的实现过程如下：
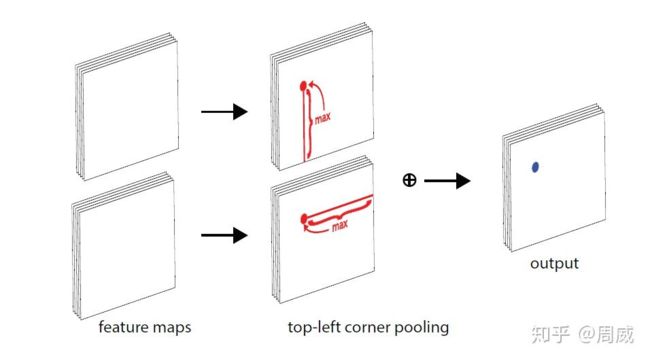图4 top-left corner pooling 的实现过程
也就是当求解某一个点的 top-left corner pooling时 ，就是以该点为起点，水平向右看遇到的最大值以及竖直向下看最大的值之和。那么对一张图上的特征值的每个像素点都执行这样的操作，看起来实属麻烦。能不能有高效的方法呢？
作者提出了一个高效的方法，如下图5
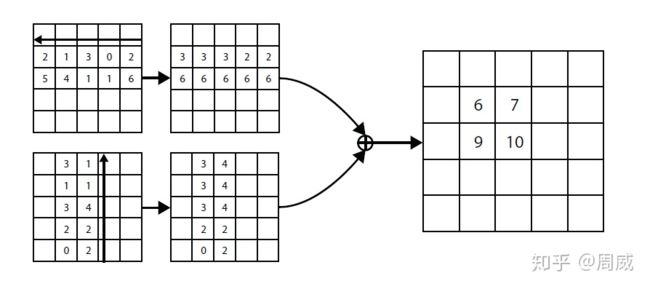图5 corner pooling高效的解决方法
图上怎么从右向左，从下向上看呢？这是bottom-right的corner pooling？
显然不是，不要被方向迷惑了。这里还是 top-left corner pooling。
把方向颠倒了后，我们每次都将沿着该方向上遇到的最大的值作为填充值即可快速实现 corner pooling。这样每行或者每列只需要进行少量的判断即可，不像之前那样，还需要每个点都要判断所沿方向上的所处行和列中的最大值，大大提升了效率。
讲到这里，相信大家应该对corner pooling进行了一些了解了。
（4）网络输出什么？各有什么作用？
我们知道网络总有六个输出，每个分支三个输出。下图为corner net的总图。从图中可以看出每个分支都有以三个构成。
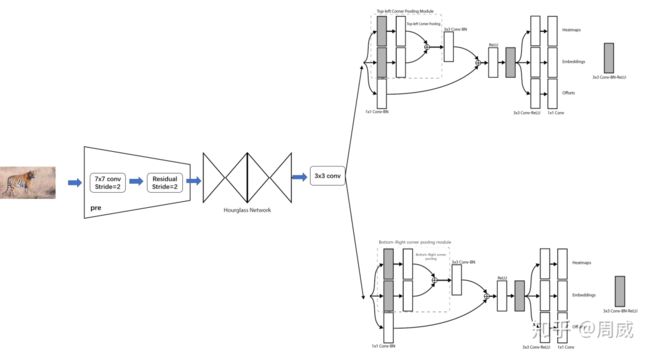
（1） heatmaps
（2） embeddings
（3） offsets
那么以上的三个输出各什么作用呢？
论文中提到
We predict two sets of heatmaps, one for top-left corners and one for bottom-right corners. Each set of heatmaps has C channels, where C is the number of categories, and is of size H ×W. There is no background channel. Each channe is a binary mask indicating the locations of the corners for a class.
那么获得的两个heatmap表示了不同类别的左上corner和右下corner的位置信息以及位置的置信度信息。
embedding输出在前面已经说过了，用来衡量左上corner和右下corner的距离的，从而判断某一对角点是否属于同一个物体的两个角点。
至于offsets输出，论文中提到
也就是heatmap被downsample至原来的1/n后，还想继续upsample回去的话会造成精度的损失，这会严重影响到小物体框的位置精度，所以作者采用了offsets来缓解这种问题。
有关这三个输出的作用就讲解结束了，基础知识就讲解完毕了。
本文将结合代码，从cornerNet的具体网络结构和损失函数开始，对cornerNet进行详细解析。
本文由于篇幅问题，就先对cornerNet的网络结构进行解析，下一篇将会对其损失函数进行详解。
3 CornerNet网络结构
cornerNet的网络结构主要分为以下几个部分
（1） backbone: hourglass Network
（2） head: 二分支输出 Top-left corners 和 Bottom-right corners，每个分支包含了各自的corner pooling以及三分支输出
以上三个部分如图6所示
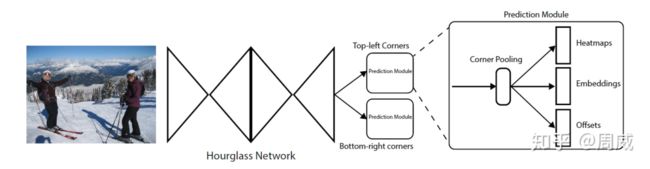图6 总结构
原文中做了很详细的解释，如下
（1）backbone: hourglass Network
上面英文的意思就是cornerNet借用了hourglass network作为他的backbone特征提取网络，这个hourglass network通常被用在姿态估计任务中，是一种呈沙漏状的downsampling 和 upsampling组合，如下图7所示为两个沙漏模块（hourglass module）头尾相连的结果。
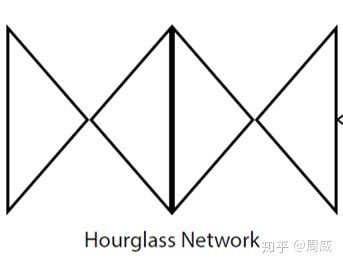图7 两个hourglass module
我们不妨借用hourglass 原文中的结构图。
图8 hourglass module 结构图
图8是一个hourglass module 的结构图。很明显地可以看出来，该网络先使用一系列卷积层和max pooling层对输入进行了downsample，然后将downsampling的特征图通过upsample layer恢复到原来输入图片的大小。
因为在max pooling的过程中会有一些细节的信息损失，所以hourglass module还采用了skip layer将特征进行融合，减少了信息的损失。
因为单个hourglass的特征提取能力是有限的，所以可以不断地进行hourglass module的堆叠，可以获得更高的特征提取能力，cornerNet中使用了两个hourglass模块。
并且在原有hourglass的基础上，作者做了以下的改进，
可以总结如下：
（1） 在输入hourglass module之前，需要将图片分辨率降低为原来的1/4倍。本文采用了一个stride=2的7x7卷积和一个stride=2的残差单元进行图片分辨率降低。
（2） 使用stride=2的卷积层代替max pooling进行downsample
（3） 共进行5次downsample ,这5次downsample后的特征图通道为[256,384,384,384,512]
（4） 采用最近邻插值的上采样（upsample),后面接两个残差单元
上述1中，会对输入图片进行一个处理，采用了一个stride=2的7x7卷积和一个stride=2的残差单元使其分辨率缩小为原来的1/4，代码实现如下
#在第一个hourglass module之前，用来降低图片分辨率为原来的1/4
self.pre = nn.Sequential(
convolution(7, 3, 128, stride=2),
residual(3, 128, 256, stride=2)
) if pre is None else pre
接着，作者提到
We apply a 3 × 3 Conv-BN module to both the input and output of the first hourglass module. We then merge them by element-wise addition followed by a ReLU and a residual block with 256 channels, which is then used as the input to the second hourglass module. The depth of the hourglass network is 104. Unlike many other state-of-the-art detectors, we only use the features from the last layer of the whole network to make predictions.
作者的意思是
（1） 在第一个hourglass module的输入和输出后都有一个3x3卷积层+BN层
（2） 然后对残差连接后使用按照元素相加
（3） 处理2完毕后，作为第二个hourglass module的输入
（4） 预测的话，只选择总网络的最后一层特征图作为输入
这里我们简单看一下代码，在models\py_utils\kp.py文件下
这里定义的类kp_module就是hourglass module的定义。
class kp_module(nn.Module):
"""
一个简单的hourglass module结构
"""
def __init__(
self, n, dims, modules, layer=residual,
make_up_layer=make_layer, make_low_layer=make_layer,
make_hg_layer=make_layer, make_hg_layer_revr=make_layer_revr,
make_pool_layer=make_pool_layer, make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer, **kwargs
):
super(kp_module, self).__init__()
self.n = n #5
# modules = [2, 2, 2, 2, 2, 4]，模块的数量
curr_mod = modules[0]
next_mod = modules[1]
# dims=[256, 256, 384, 384, 384, 512]
curr_dim = dims[0]
next_dim = dims[1]
self.up1 = make_up_layer(
3, curr_dim, curr_dim, curr_mod,
layer=layer, **kwargs
) #三个简单的layer(residual module),kernel_size=3
self.max1 = make_pool_layer(curr_dim) #MaxPool2d(kernel_size=2, stride=2)
self.low1 = make_hg_layer(
3, curr_dim, next_dim, curr_mod,
layer=layer, **kwargs
) #三个简单的layer(residual module),kernel_size=3
self.low2 = kp_module(
n - 1, dims[1:], modules[1:], layer=layer,
make_up_layer=make_up_layer,
make_low_layer=make_low_layer,
make_hg_layer=make_hg_layer,
make_hg_layer_revr=make_hg_layer_revr,
make_pool_layer=make_pool_layer,
make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer,
**kwargs
) if self.n > 1 else \
make_low_layer(
3, next_dim, next_dim, next_mod,
layer=layer, **kwargs
) #递归的思想，不断地降低n,知道n>1不满足
self.low3 = make_hg_layer_revr(
3, next_dim, curr_dim, curr_mod,
layer=layer, **kwargs
)
# nn.Upsample(scale_factor=2)
self.up2 = make_unpool_layer(curr_dim)
self.merge = make_merge_layer(curr_dim)
def forward(self, x):
up1 = self.up1(x)
max1 = self.max1(x)
low1 = self.low1(max1)
low2 = self.low2(low1)
low3 = self.low3(low2)
up2 = self.up2(low3)
return self.merge(up1, up2) #element-wise add
我们注意到self.low2的定义如下
self.low2 = kp_module(
n - 1, dims[1:], modules[1:], layer=layer,
make_up_layer=make_up_layer,
make_low_layer=make_low_layer,
make_hg_layer=make_hg_layer,
make_hg_layer_revr=make_hg_layer_revr,
make_pool_layer=make_pool_layer,
make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer,
**kwargs
) if self.n > 1 else \
make_low_layer(
3, next_dim, next_dim, next_mod,
layer=layer, **kwargs
) #递归的思想，不断地降低n,知道n>1不满足
这里是在kp_module的类定义中使用了它本身。很明显这是一个递归的思想。有了这个递归的思想，这个hourglass module就定义就很容易进行实现和理解了。
定义结束hourglass module后，定义由两个hourglass module构成的hourglass网络，代码如下：
self.kps = nn.ModuleList([
kp_module(
n, dims, modules, layer=kp_layer,
make_up_layer=make_up_layer,
make_low_layer=make_low_layer,
make_hg_layer=make_hg_layer,
make_hg_layer_revr=make_hg_layer_revr,
make_pool_layer=make_pool_layer,
make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer
) for _ in range(nstack) #hourglass 网络，包含了nstack个模块
])
至此，特征提取网络（backbone）— hourglass 就定义结束了。
(2) head: 二分支输出 Top-left corners 和 Bottom-right corners
通过两个hourglass module后的特征图，需要各自再通过一个3x3卷积后才能获得两个corners分支。如下图所示。
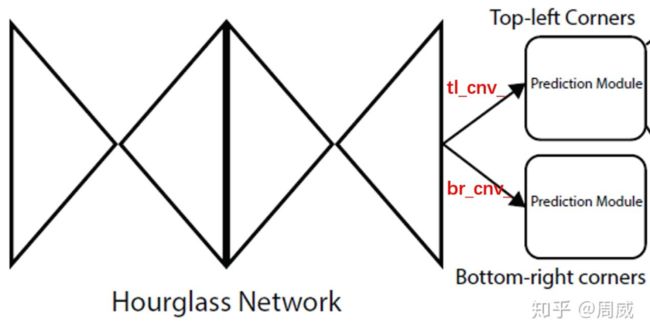图9 双分支
代码实现如下：
# 获得两个分支特征图，分别做左上点和右下点的预测的
tl_cnv = tl_cnv_(cnv)
br_cnv = br_cnv_(cnv)
获得用于预测左上点和右下点的两个分支module（就是图上的prediction module)后，每个predicition module分别进行如下操作
（1） corner pooling
（2） 三分支的输出
这里以top_left corners的prediction module为例，如图10所示。
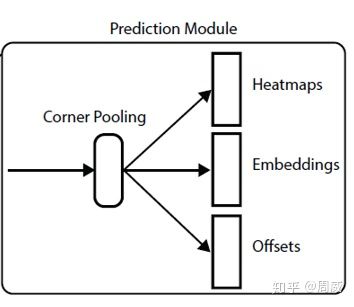图 10
更具体地，这里仍然根据论文中的图，如下图11是图10的具体实现。
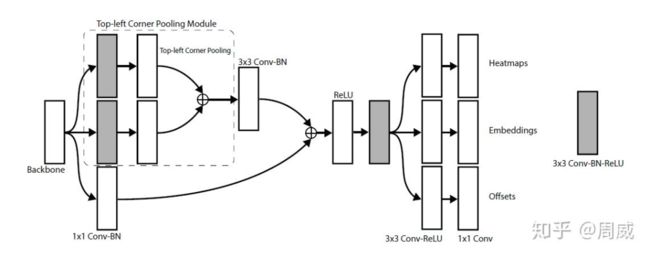图11
具有有关上面代码中的tl_cnv_实现如下，这其实就是一个实例化的tl_pool类（top-left corner pooling )。有关代码定义如下
class tl_pool(pool):
def __init__(self, dim):
super(tl_pool, self).__init__(dim, TopPool, LeftPool)
他是pool的子类，pool定义如下
class pool(nn.Module):
def __init__(self, dim, pool1, pool2):
super(pool, self).__init__()
self.p1_conv1 = convolution(3, dim, 128)
self.p2_conv1 = convolution(3, dim, 128)
self.p_conv1 = nn.Conv2d(128, dim, (3, 3), padding=(1, 1), bias=False)
self.p_bn1 = nn.BatchNorm2d(dim)
self.conv1 = nn.Conv2d(dim, dim, (1, 1), bias=False)
self.bn1 = nn.BatchNorm2d(dim)
self.relu1 = nn.ReLU(inplace=True)
self.conv2 = convolution(3, dim, dim)
self.pool1 = pool1()
self.pool2 = pool2()
def forward(self, x):
# pool 1
p1_conv1 = self.p1_conv1(x)
pool1 = self.pool1(p1_conv1)
# pool 2
p2_conv1 = self.p2_conv1(x)
pool2 = self.pool2(p2_conv1)
# pool 1 + pool 2
p_conv1 = self.p_conv1(pool1 + pool2)
p_bn1 = self.p_bn1(p_conv1)
# resudual connect
conv1 = self.conv1(x)
bn1 = self.bn1(conv1)
relu1 = self.relu1(p_bn1 + bn1)
conv2 = self.conv2(relu1)
return conv2
很清晰明了，这代码就是图11中部分实现，该部分如图12所示。
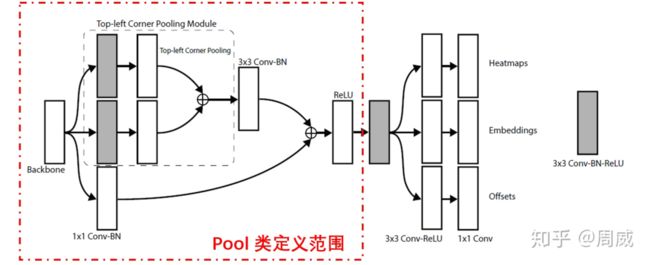图 12
那么根据上述代码执行后的结果，对其分别执行3x3 conv-BN-ReLU后，获得三个输出。代码实现如下:
#对上面两个分支分别输出三个预测分支
tl_heat, br_heat = tl_heat_(tl_cnv), br_heat_(br_cnv)
tl_tag, br_tag = tl_tag_(tl_cnv), br_tag_(br_cnv)
tl_regr, br_regr = tl_regr_(tl_cnv), br_regr_(br_cnv)
至此，有关corner net的网络就解析完毕了，我们根据代码绘制一张总的模型图，如图13所示。
图 13
4 总结
本文结合论文和代码对CornerNet的网络结构进行详细解析。如果哪里出现错误（错别字或者认识上的偏差），欢迎批评指正！下一篇将对cornerNet的损失函数进行详细解析。
