数字正交下变频(低通滤波法)
[TOC]
数字正交下变频原理
在通信系统或雷达系统中,正交下变频是一个比较重要的概念。本文对数字正交下变频的原理相关介绍并进行了仿真。而在此之前,需要数字正交上变频和带通采样定理的一些先验知识,下文都进行了相关介绍。
数字正交上变频
在讨论数字正交下变频的过程中,不可避免的要了解接收机数字下变频系统的输入信号形式,这时候就必须熟悉通信系统发射机所发射的信号形态,下面对此进行讨论。

图1.1 数字正交上变频
图中 I(t) 为信号同相部分,Q(t)为信号正交部分。而 S(t)=I(t)cos(2πf0t)−Q(t)cos(2πf0t) ,该信号就是发射机的发射信号(实际过程中发射信号还会再进行一次混频,将信号混频至高频信号进行发射,以减少在信号在传输过程中的信号衰减)。
数字正交上变频系统的输出包含了信号的同相部分和正交部分,即包含了信号的幅度信息和相位信息,便于后续的信号处理。
那么为什么信号需要处理成这种形式发射呢?这是因为我们在信号处理的过程中,一般采用的是复数解析信号,这样可以知道严格的信号相位关系,消除频域负半轴上镜频的影响,便于信号处理。而实际发射的波形只可能是实数信号,故才会有这种形式,具体推导如下:
S(t)=Re{[I(t)+jQ(t)]ej2πf0t} =Re{[I(t)+jQ(t)][cos(2πf0t)+jsin(2πf0t)]} =I(t)cos(2πf0t)−Q(t)cos(2πf0t)
数字正交下变频
上一节介绍了数字正交上变频的原理,推导了正交上变频系统的输出。而数字正交下变频系统的任务便是去除接收信号中的中频载波,无损的提取出信号的同相部分和正交部分。数字正交下变频包括三种方式,分别为低通滤波法,插值法和多相滤波法。本文主要介绍低通滤波法,原理图如下所示。

图1.2 数字正交下变频
如图1.2所示,相干检波的同相和正交输出分别为
SI0(t)=S0(t)cos(2∗πf0t)=[I(t)cos(2πf0t)−Q(t)cos(2πf0t)]⋅cos(2πf0t) =12I(t)+12I(t)cos(2π⋅2f0t)−12Q(t)sin(2π⋅2f0t)
SQ0(t)=−S0(t)sin(2∗πf0t)=−[I(t)cos(2πf0t)−Q(t)cos(2πf0t)]⋅sin(2πf0t) =12Q(t)+12I(t)sin(2π⋅2f0t)−12Q(t)cos(2π⋅2f0t)
两条支路相干检波的结果再进行低通滤波就可以得到信号的同相部分和正交部分结果。从而可以进一步组合成复数解析信号,进行后续的进一步处理。
I∧(t)=12I(t)
Q∧(t)=12Q(t)
带通采样定理
在数字下变频系统中,由于输入信号包含一个中频载波,信号会根据载波频率进行频移,得到一个带限信号。如果此时仍然采用奈奎斯特采样定理,采样频率为信号最高频率的两倍,那么此时所需的采样频率将会很高,增加接收机设计的复杂度。此时我们采用带宽采样定理,下面是具体推导过程。
采样过程中需要注意的便是采样之后,信号的频谱不能混叠,这样通过一定的滤波手段可以无损的恢复原始信号。带限信号采样过程如下所示。

图1.3 带通采样定理
如图1.3所示, fH 和 fL 分别为带限信号的最高频率和最低频率,有如下关系
fL+fH=2f0
fH−fL=B
假设以采样频率对信号进行采样,那么在频域就表示为对信号以 fs 为周期进行频移。
假设当第 n 次频移时,信号负频部分刚好移动至信号正频部分右方,此时应满足:
−fH+nfs≥fH
而为保证信号频谱不混叠,那么第 n 次频移后信号必须保证在正频部分的左边,此时应满足:
−fL+(n−1)fs≤fL
即采样频率应满足如下条件:
2fHn≤fs≤2fLn−1
记得以前看过采样频率和中频是满足一个等式条件,其实那个等式是采样频率的一个最佳值,是通过插值的方式推导出来的,理论上采样频率只要满足上面的不等式就可以了。
正交下变频仿真
以雷达系统为例,对数字正交下变频进行仿真,仿真参数如下所示。
| 参数 | 名称 | 取值 | 备注 |
|---|---|---|---|
| f0 | 中频 | 20MHz | |
| B | 带宽 | 2MHz | |
| tau | 时宽 | 150us | |
| T | 重复周期 | 2ms | |
| fs | 采样频率 | 15MHz | |
| SNR | 信噪比 | 20dB | |
| dis | 目标距离 | T*f_s/2 | 将目标设置在回波距离段中间 |
关于上面表格中的采样频率设置,可根据上一节中的推导结果进行设置,下面表格给出一些可能情况。
2fHn≤fs≤2fLn−1
| n 取值 | fs 取值 |
|---|---|
| 2 | (21,38) |
| 3 | (14,19) |
| 4 | (10.5,12.6) |
| 5 | (8.4,9.5) |
| 6 | (7,7.6) |
| …… | …… |
采样频率可取上面表格中区间内的任何值,为使硬件处理方便,通常选取与中频存在倍数关系的取值。
根据相关参数,首先仿真理想的线性调频信号进行发射机信号调制的结果如下图所示:

图2.1 调制后的线性调频信号
将该信号放置在回波中段,并添加高斯白噪声,模拟接收机接收的中频信号,如下图所示。

图2.2 回波信号
对回波信号进行混频,得到同相部分和正交部分。

图2.3 混频后信号
而后进行低通滤波,滤波器用hamming窗进行设计,阶数为127,其幅频特性和相频特性如下所示。

图2.3 FIR滤波器幅频/相频特性
经过低通滤波后,得到可用于后续信号处理的基带信号,如下所示
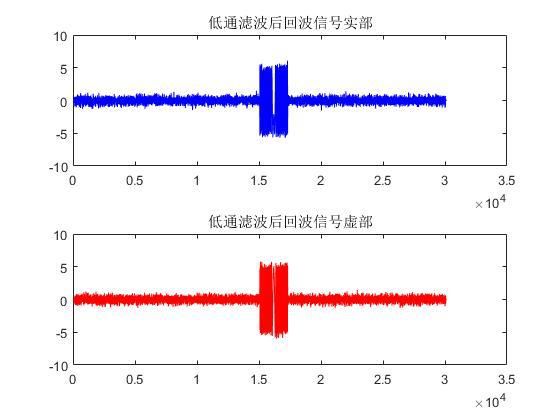
图2.3 基带信号
以上便是正交下变频的仿真过程,具体代码可参见附录。
而这里进一步讨论采样频率的选取对结果的影响。上面的仿真采用的采样频率为 15MHz ,此时落入 n=3 时的 (14Mhz,19MHz) 区间中。我们换用一个较大的采样频率 20MHz ,但是并未落入采样频率任何取值区间(参见表1.1),得到的最终结果如下。

图2.4 不满足带通采样定理基带信号
很明显看出,此时滤波结果与正常结果间存在较大的偏差,这是由于采样频率的选取造成了频谱混叠。
仿真代码附录
%% DDC
clear ; close all; clc;
% parameter
f0 = 20e+6; % 20MHz中频
B = 2e+6; % 2MHz带宽
Tao = 150e-6; % 200us时宽
T = 2e-3; % 2ms脉冲重复周期
fs = 15e+6; % 15MHz采样频率
SNR = 20; % 信噪比20dB
dis = T*fs/2; % 将目标设置在回波中间处
% Generate LFM @f0
t = -round(Tao*fs/2):1:round(Tao*fs/2)-1; % 脉冲采样点
median_fre = (10^(SNR/20))* (cos(pi*B/Tao*(t/fs).^2 ).*cos(2*pi*f0*t/fs) - sin(pi*B/Tao*(t/fs).^2 ).*sin(2*pi*f0*t/fs)); % I*cos + Q*sin
figure;
plot(median_fre); title('进行调制后的线性调频信号');
% Generate echo
echo = zeros(1,T*fs);
echo(dis:1:dis+Tao*fs-1) = median_fre;
noise = normrnd(0,1,1,T*fs);
% noise = 0.5*ones(1,T*fs);
echo = echo + noise;
figure;plot(echo); title('回波信号'); % 实际的回波信号,只有实部
% frequence mixing
echo = echo.*exp(-1i*2*pi*f0*(0:1:T*fs-1)/fs);
figure;
subplot(2,1,1); plot(real(echo),'b'); title('混频后回波信号实部');
subplot(2,1,2); plot(imag(echo),'r'); title('混频后回波信号虚部');
figure; plot(abs(fftshift(fft(echo)))); title('混频后回波信号频谱');
% Generate low pass filter coeff
coeff = fir1(127,B/(fs/2),hamming(128)); % 0.4 = B/(fs/2)
figure;freqz(coeff);
% fir filter
ddc_res = conv(echo,coeff);
figure;
subplot(2,1,1); plot(real(ddc_res),'b'); title('低通滤波后回波信号实部');
subplot(2,1,2); plot(imag(ddc_res),'r'); title('低通滤波后回波信号虚部');