Double Array Trie

Trie树主要应用在信息检索领域，非常高效。今天我们讲Double Array Trie，请先把Trie树忘掉，把信息检索忘掉，我们来讲一个确定有限自动机（deterministic finite automaton ，DFA）的故事。所谓“确定有限自动机”是指给定一个状态和一个变量时，它能跳转到的下一个状态也就确定下来了，同时状态是有限的。请注意这里出现两个名词，一个是“状态”，一个是“变量”，下文会举例说明这两个名词的含义。

举个例子，假设我们一共有10个汉字，每个汉字就是一个“变量”。我们为每个汉字编个序号。

 

1	2	3	4	5	6	7	8	9	10
啊	阿	埃	根	胶	拉	及	廷	伯	人

             表1. “变量”的编号

这10个汉字一共可以构成6个词语：啊，埃及，阿胶，阿根廷，阿拉伯，阿拉伯人。　　　　　　　　　

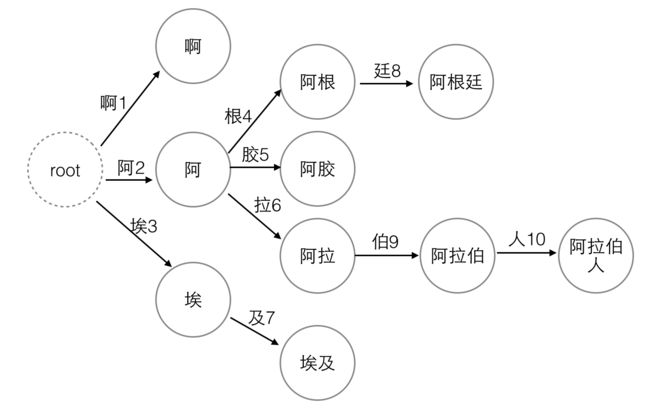
这里的每个词以及它的任意前缀都是一个“状态”，“状态”一共有10个：啊,阿,埃,阿根,阿根廷,阿胶,阿拉,阿拉伯,阿拉伯人,埃及

我们把DFA图画出来:

　　　　　　　　图1. DFA，同时也是Trie树

在图中每个节点代表一个“状态”，每条边代表一个“变量”，并且我们把变量的编号也标在了图中。

下面我们构造两个int数组：base和check，它们的长度始终是一样的。数组的长度定多少并没有严格的规定，反正随着词语的插入，数组肯定是要扩容的。说到数组扩容，大家可以看一下java中HashMap的扩容策略，每次扩容数组的长度都会变为2的整次幂。HashMap中有这么一个精妙的函数：

//给定一个整数，返回大于等于这个数的2的整次幂
static int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 :  n + 1;
}

回到今天的正题，我们不妨把double array的初始长度就定得大一些。两数组元素初始值均为0。

double array的初始状态：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
state

把词添加到词典的过程就给base和check数组中各元素赋值的过程。下面我们层次遍历图1所示的Trie树。

step1.

第一层上取到3个“状态”：啊,阿,埃。把这3个状态按照其对应的变量的编号（查表1）放到state数组中。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃

step2.

当存在状态转移时，有

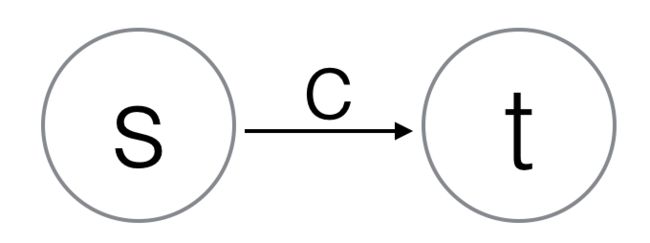
check[t]=s
base[s]+c=t

其中s和t代表某个状态在数组中的下标，c代表变量的编号。

此时层次遍历来到了图1所示DFA的第二层，我们看到“阿”的子节点有“阿根”、“阿胶”、“阿拉”，已知状态“阿”的下标是2，变量“根”、“胶”、“拉”的编号依次是4、5、6，下面我们要给base[2]赋值：从小到大遍历所有的正整数，直到发现某个数正整k满足base[k+4]=base[k+5]=base[k+6]=check[k+4]=check[k+5]=check[k+6]=0。得到k=1，那么就把1赋给base[2]，同时也确定了状态“阿根”、“阿胶”、“阿拉”的下标依次是k+4、k+5、k+6，即5、6、7，而且check[5]=check[6]=check[7]=2。

同理，“埃”的子节点是“埃及”，状态“埃”的下标是3，变量“及”的编号是7，此时有check[1+7]=base[1+7]=0，所以base[3]=1，状态“埃及”的下标是8，check[8]=3。

遍历完DFA的第二层后得到下表：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	0	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及

step3.

重复step2，层次遍历完整查询树之后，得到：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	0	1	1	0	1	0	1	0	0	1	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	10	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉伯	阿拉伯人

step4.

最后遍历一次DFA，当某个节点已经是一个词的结尾时，按下列方法修改其base值。

if(base[i]==0)
    base[i]=-i
else
    base[i]=-base[i]

得到：

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	1	-8	-9	-1	-11	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	10	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉伯	阿拉伯人

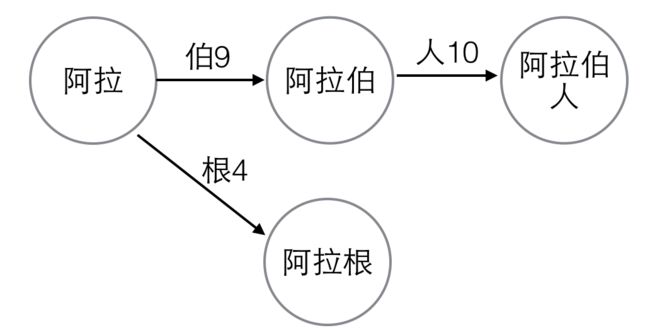
double array建好之后，如果词典中又动态地添加了一个新词，比如“阿拉根”，那么“阿拉”的所有子孙节点在double array中的位置要重新分配。

 

图2. 动态添加一个词

首先，把“阿拉伯”和“阿拉伯人”对应的base、check值清0，把“阿拉伯”和“阿拉伯人”从state数组中删除掉，把“阿拉”的base值清0。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	0	-8	-9	0	0	0	0	0	0	0	0	0	0
check	0	0	0	0	2	2	2	3	5	0	0	0	0	0	0	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷

然后，按照上面step2所述的方法把“阿拉伯”、“阿拉根”插入到double array中。变量“根”、“伯”的编号是4和9，满足base[k+4]=base[k+9]=check[k+4]=check[k+9]=0的最小的k是6，所以base[7]=6，“阿拉伯”和“阿拉根”对应的下标是10和15。同理把“阿拉伯人”插入到double array中。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	6	-8	-9	0	0	0	0	0	1	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	15	0	0	0	7	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉根	阿拉伯人				阿拉伯

最后，遍历图2所示的DFA，当某个节点已经是一个词的结尾时按照step4中的方法修改其base值。

下标	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
base	-1	1	1	0	1	-6	6	-8	-9	-10	-11	0	0	0	-1	0	0	0	0
check	0	0	0	0	2	2	2	3	5	7	15	0	0	0	7	0	0	0	0
state	啊	阿	埃		阿根	阿胶	阿拉	埃及	阿根廷	阿拉根	阿拉伯人				阿拉伯

 

double array建好之后，如何查询一个词是否在词典中呢？

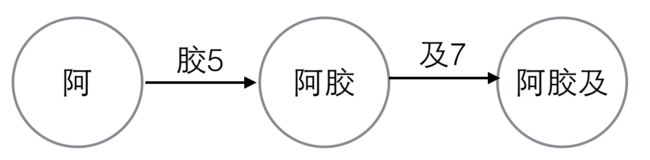
比如要查“阿胶及”，每个字的编号是已知的，我们画出状态转移图。

变量“阿”的编号是2，base[2]=1，变量“胶”的编号是5，base[2]+5=6，我们检查一下check[6]是否等于2。check[6]确实等于2，则继续看下一个状态转移。同时我们发现base[6]是负数，这说明“阿胶”已经是一个完整的词了。

继续看下一个状态转移，base[6]=-6，负数取其相反数，base[6]=6，变量“及”的编号是7，base[6]+7=13，我们检查一下check[13]是否等于6，发现不满足，则“阿胶及”不是一个词，甚至都是不是任意一个词的前缀。

github上一个日本人贡献了他的java版的Darts(Darts本来是一种Double Array Trie的C++实现)，代码如下：

import java.io.BufferedInputStream;
import java.io.BufferedOutputStream;
import java.io.DataInputStream;
import java.io.DataOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileOutputStream;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

/**
 * DoubleArrayTrie在构建双数组的过程中也借助于一棵传统的Trie树，但这棵Trie树并没有被保存下来，
 * 如果要查找以prefix为前缀的所有词不适合用DoubleArrayTrie，应该用传统的Trie树。
 * 
 * @author zhangchaoyang
 *
 */
public class DoubleArrayTrie {
	private final static int BUF_SIZE = 16384;// 2^14，java采用unicode编码表示所有字符，每个字符固定用两个字节表示。考虑到每个字节的符号位都是0，所以又可以节省两个bit
	private final static int UNIT_SIZE = 8; // size of int + int

	private static class Node {
		int code;// 字符的unicode编码
		int depth;// 在Trie树中的深度
		int left;//
		int right;//
	};

	private int check[];
	private int base[];

	private boolean used[];
	private int size;
	private int allocSize;// base数组当前的长度
	private List key;// 所有的词
	private int keySize;
	private int length[];
	private int value[];
	private int progress;
	private int nextCheckPos;
	int error_;

	// 扩充base和check数组
	private int resize(int newSize) {
		int[] base2 = new int[newSize];
		int[] check2 = new int[newSize];
		boolean used2[] = new boolean[newSize];
		if (allocSize > 0) {
			System.arraycopy(base, 0, base2, 0, allocSize);// 如果allocSize超过了base2的长度，会抛出异常
			System.arraycopy(check, 0, check2, 0, allocSize);
			System.arraycopy(used, 0, used2, 0, allocSize);
		}

		base = base2;
		check = check2;
		used = used2;

		return allocSize = newSize;
	}

	private int fetch(Node parent, List siblings) {
		if (error_ < 0)
			return 0;

		int prev = 0;

		for (int i = parent.left; i < parent.right; i++) {
			if ((length != null ? length[i] : key.get(i).length()) < parent.depth)
				continue;

			String tmp = key.get(i);

			int cur = 0;
			if ((length != null ? length[i] : tmp.length()) != parent.depth)
				cur = (int) tmp.charAt(parent.depth) + 1;

			if (prev > cur) {
				error_ = -3;
				return 0;
			}

			if (cur != prev || siblings.size() == 0) {
				Node tmp_node = new Node();
				tmp_node.depth = parent.depth + 1;
				tmp_node.code = cur;
				tmp_node.left = i;
				if (siblings.size() != 0)
					siblings.get(siblings.size() - 1).right = i;

				siblings.add(tmp_node);
			}

			prev = cur;
		}

		if (siblings.size() != 0)
			siblings.get(siblings.size() - 1).right = parent.right;

		return siblings.size();
	}

	private int insert(List siblings) {
		if (error_ < 0)
			return 0;

		int begin = 0;
		int pos = ((siblings.get(0).code + 1 > nextCheckPos) ? siblings.get(0).code + 1
				: nextCheckPos) - 1;
		int nonzero_num = 0;
		int first = 0;

		if (allocSize <= pos)
			resize(pos + 1);

		outer: while (true) {
			pos++;

			if (allocSize <= pos)
				resize(pos + 1);

			if (check[pos] != 0) {
				nonzero_num++;
				continue;
			} else if (first == 0) {
				nextCheckPos = pos;
				first = 1;
			}

			begin = pos - siblings.get(0).code;
			if (allocSize <= (begin + siblings.get(siblings.size() - 1).code)) {
				// progress can be zero
				double l = (1.05 > 1.0 * keySize / (progress + 1)) ? 1.05 : 1.0
						* keySize / (progress + 1);
				resize((int) (allocSize * l));
			}

			if (used[begin])
				continue;

			for (int i = 1; i < siblings.size(); i++)
				if (check[begin + siblings.get(i).code] != 0)
					continue outer;

			break;
		}

		// -- Simple heuristics --
		// if the percentage of non-empty contents in check between the
		// index
		// 'next_check_pos' and 'check' is greater than some constant value
		// (e.g. 0.9),
		// new 'next_check_pos' index is written by 'check'.
		if (1.0 * nonzero_num / (pos - nextCheckPos + 1) >= 0.95)
			nextCheckPos = pos;

		used[begin] = true;
		size = (size > begin + siblings.get(siblings.size() - 1).code + 1) ? size
				: begin + siblings.get(siblings.size() - 1).code + 1;

		for (int i = 0; i < siblings.size(); i++)
			check[begin + siblings.get(i).code] = begin;

		for (int i = 0; i < siblings.size(); i++) {
			List new_siblings = new ArrayList();

			if (fetch(siblings.get(i), new_siblings) == 0) {
				base[begin + siblings.get(i).code] = (value != null) ? (-value[siblings
						.get(i).left] - 1) : (-siblings.get(i).left - 1);

				if (value != null && (-value[siblings.get(i).left] - 1) >= 0) {
					error_ = -2;
					return 0;
				}

				progress++;
				// if (progress_func_) (*progress_func_) (progress,
				// keySize);
			} else {
				int h = insert(new_siblings);
				base[begin + siblings.get(i).code] = h;
			}
		}
		return begin;
	}

	public DoubleArrayTrie() {
		check = null;
		base = null;
		used = null;
		size = 0;
		allocSize = 0;
		// no_delete_ = false;
		error_ = 0;
	}

	// no deconstructor

	// set_result omitted
	// the search methods returns (the list of) the value(s) instead
	// of (the list of) the pair(s) of value(s) and length(s)

	// set_array omitted
	// array omitted

	void clear() {
		// if (! no_delete_)
		check = null;
		base = null;
		used = null;
		allocSize = 0;
		size = 0;
		// no_delete_ = false;
	}

	public int getUnitSize() {
		return UNIT_SIZE;
	}

	public int getSize() {
		return size;
	}

	public int getTotalSize() {
		return size * UNIT_SIZE;
	}

	public int getNonzeroSize() {
		int result = 0;
		for (int i = 0; i < size; i++)
			if (check[i] != 0)
				result++;
		return result;
	}

	public int build(List key) {
		return build(key, null, null, key.size());
	}

	public int build(List _key, int _length[], int _value[],
			int _keySize) {
		if (_keySize > _key.size() || _key == null)
			return 0;

		// progress_func_ = progress_func;
		key = _key;
		length = _length;
		keySize = _keySize;
		value = _value;
		progress = 0;

		resize(65536 * 32);

		base[0] = 1;
		nextCheckPos = 0;

		Node root_node = new Node();
		root_node.left = 0;
		root_node.right = keySize;
		root_node.depth = 0;

		List siblings = new ArrayList();
		fetch(root_node, siblings);
		insert(siblings);

		// size += (1 << 8 * 2) + 1; // ???
		// if (size >= allocSize) resize (size);

		used = null;
		key = null;

		return error_;
	}

	public void open(String fileName) throws IOException {
		File file = new File(fileName);
		size = (int) file.length() / UNIT_SIZE;
		check = new int[size];
		base = new int[size];

		DataInputStream is = null;
		try {
			is = new DataInputStream(new BufferedInputStream(
					new FileInputStream(file), BUF_SIZE));
			for (int i = 0; i < size; i++) {
				base[i] = is.readInt();
				check[i] = is.readInt();
			}
		} finally {
			if (is != null)
				is.close();
		}
	}

	public void save(String fileName) throws IOException {
		DataOutputStream out = null;
		try {
			out = new DataOutputStream(new BufferedOutputStream(
					new FileOutputStream(fileName)));
			for (int i = 0; i < size; i++) {
				out.writeInt(base[i]);
				out.writeInt(check[i]);
			}
			out.close();
		} finally {
			if (out != null)
				out.close();
		}
	}

	public int exactMatchSearch(String key) {
		return exactMatchSearch(key, 0, 0, 0);
	}

	public int exactMatchSearch(String key, int pos, int len, int nodePos) {
		if (len <= 0)
			len = key.length();
		if (nodePos <= 0)
			nodePos = 0;

		int result = -1;

		char[] keyChars = key.toCharArray();

		int b = base[nodePos];
		int p;

		for (int i = pos; i < len; i++) {
			p = b + (int) (keyChars[i]) + 1;
			if (b == check[p])
				b = base[p];
			else
				return result;
		}

		p = b;
		int n = base[p];
		if (b == check[p] && n < 0) {
			result = -n - 1;
		}
		return result;
	}

	public List commonPrefixSearch(String key) {
		return commonPrefixSearch(key, 0, 0, 0);
	}

	public List commonPrefixSearch(String key, int pos, int len,
			int nodePos) {
		if (len <= 0)
			len = key.length();
		if (nodePos <= 0)
			nodePos = 0;

		List result = new ArrayList();

		char[] keyChars = key.toCharArray();

		int b = base[nodePos];
		int n;
		int p;

		for (int i = pos; i < len; i++) {
			p = b;
			n = base[p];

			if (b == check[p] && n < 0) {
				result.add(-n - 1);
			}

			p = b + (int) (keyChars[i]) + 1;
			if (b == check[p])
				b = base[p];
			else
				return result;
		}

		p = b;
		n = base[p];

		if (b == check[p] && n < 0) {
			result.add(-n - 1);
		}

		return result;
	}

	// debug
	public void dump() {
		for (int i = 0; i < size; i++) {
			System.err.println("i: " + i + " [" + base[i] + ", " + check[i]
					+ "]");
		}
	}
}

 

public class TestDoubleArrayTrie {

	/**
	 * 检索key的前缀命中了词典中的哪些词

	 * key的前缀有多个，所以有可能命中词典中的多个词
	 */
	@Test
	public void testPrefixMatch() {
		DoubleArrayTrie adt = new DoubleArrayTrie();
		List list = new ArrayList();
		list.add("阿胶");
		list.add("阿拉伯");
		list.add("阿拉伯人");
		list.add("埃及");
		// 所有词必须先排序
		Collections.sort(list);
		// 构建DoubleArrayTrie
		adt.build(list);
		String key = "阿拉伯人";
		// 检索key的前缀命中了词典中的哪些词
		List rect = adt.commonPrefixSearch(key);
		for (int index : rect) {
			System.out.println("前缀  " + list.get(index) + " matched");
		}
		System.out.println("=================");
	}

	/**
	 * 检索key是否完全命中了词典中的某个词
	 */
	@Test
	public void testFullMatch() {
		DoubleArrayTrie adt = new DoubleArrayTrie();
		List list = new ArrayList();
		list.add("阿胶");
		list.add("阿拉伯");
		list.add("阿拉伯人");
		list.add("埃及");
		// 所有词必须先排序
		Collections.sort(list);
		// 构建DoubleArrayTrie
		adt.build(list);
		String key = "阿拉";
		// 检索key是否完全命中了词典中的某个词
		int index = adt.exactMatchSearch(key);
		if (index >= 0) {
			System.out.println(key + " match " + list.get(index));
		} else {
			System.out.println(key + " not match any term");
		}
		key = "阿拉伯";
		index = adt.exactMatchSearch(key);
		if (index >= 0) {
			System.out.println(key + " match " + list.get(index));
		} else {
			System.out.println(key + " not match any term");
		}
		key = "阿拉伯人";
		index = adt.exactMatchSearch(key);
		if (index >= 0) {
			System.out.println(key + " match " + list.get(index));
		} else {
			System.out.println(key + " not match any term");
		}
		System.out.println("=================");
	}
}