狄利克雷分布、采样方法、主题模型

Gamma函数

• 公式
  $$\Gamma (x)={\int }_0^{+\infty }{e}^{-t}{t}^{x-1}dt$$
• 性质

$$\Gamma (x+1)=x\Gamma (x)$$
$$\Gamma (n)=(n-1)!$$

Beta函数

• 公式
  $$\mathrm{B}(m,n)={\int }_0^1{x}^{m-1}(1-x{)}^{n-1}dx$$
• 性质

$$\mathrm{B}(m,n)=\frac{\Gamma (m)\Gamma (n)}{\Gamma (m+n)}$$

二项分布

• 假设在玩CS游戏，你拿着狙击枪，敌人出现你打中敌人的概率是P,打不中敌人的概率是1-P,那么敌人第一次出现你没打中，而第二次出现你打中的概率是(1-P)P。如果敌人出现了n词，而你打中了其k次，而不确定具体是哪k次，这样从n次中任取k次的次数是$C_n^k$,而这不确定k次打中敌人的概率是$C_n^k{p}^k(1-p{)}^{n-k}$，通过这个例子可以得知二项分布的概率：

  $$f(k;n,p)=C_n^k{p}^k(1-p{)}^{n-k}$$

Beta分布

• 定义

$$f(x;a,\beta )=\frac{x^{a-1}(1-x{)}^{\beta -1}}{{\int }_0^1{u}^{a-1}(1-u{)}^{\beta -1}du}$$
$$=\frac{x^{a-1}(1-x{)}^{\beta -1}}{\mathrm{B}(a,\beta )}$$
$$=\frac{\Gamma (a+\beta )}{\Gamma (a)\Gamma (\beta )}{x}^{a-1}(1-x{)}^{\beta -1}$$

• 期望

$$E(p)={\int }_0^1\frac{p^a(1-p{)}^{\beta -1}dp}{\Gamma (a,\beta )}=\frac{\mathrm{B}(a+1,\beta )}{\mathrm{B}(a,\beta )}$$
$$=\frac{\Gamma (a+1)\Gamma (\beta )}{\Gamma (a+\beta +1)}\frac{\Gamma (a+\beta )}{\Gamma (a)\Gamma (\beta )}$$
$$=\frac{a}{a+\beta }$$

• 相似分布

  如果$p服从分布Dir(t|a)$则可证明,
  $$E(p)=(\frac{a_1}{{\sum }_i{a}_i},\frac{a_2}{{\sum }_i{a}_i},\cdots )$$

• 多项分布

  设投掷n次骰子，这个骰子共有六种结果，且1点出现概率为$p_1$,2点出现概率为$p_2,\cdots$多项分布给出了在n次实验中，骰子1点出现$x_1$次，2点出现$x_2$次，3点出现$x_3$次，$\cdots$,6点出现$x_6$次，这个结果组合的概率为：
  $$\frac{n!}{x_1!x_2!\cdots x_k!}{p}_1^{x_1}{p}_2^{x_2}\cdots p_k^{x_k}$$
  亦可表示为：
  $$\frac{\Gamma ({\sum }_i{x}_i+1)}{{\prod }_i\Gamma (x_i+1)}\prod _i{p}_i^{x_i}$$

狄利克雷分布

• 狄利克雷分布式beta分布在多项式情况下的情况，也就是多项分布的共轭先验分布，其概率密度如下：
  $$f(p_1,p_2,\cdots ,p_{k-1}|a_1,a_2,\cdots ,a_k)=\frac{1}{\Delta (a)}\prod _{i=1}^k{p}^{a_i-1}$$
  其中的$\Delta (a)$计算公式如下：
  $$\Delta (a)=\frac{{\prod }_{i=1}^k\Gamma (a_i)}{\Gamma ({\sum }_i{a}_i)}$$

共轭先验分布

• 所谓共轭，知识我们选取一个函数作为似然函数的先验分布，使得后验分布函数和先验分布函数形式一致。比如Beta分布是二项分布的共轭先验概率分布，而狄更斯分布式多项式分布的共轭先验概率分布。

1. 参数估计

   对于典型的离散型随机变量分布：二项分布、多项分布；典型的连续性随机变量分布：正态分布。他们都可以看作参数分布，因为他们的函数形式被一小部分参数控制，比如正态分布的均值合方差，二项分布事件发生的概率等。因此，给定一堆观测数据集，我们需要有一个解决方案来确定这些参数值的大小，以便能够利用分布模型做密度估计，这就是参数估计。
   对于参数估计，一直存在两个学派的不同解决方案。一是频率学派解决方案：通过某些优化准则来选定特定参数值；二是贝叶斯学派方案：假定参数服从一个先验分布，通过观测到的数据，使用被也是理论计算对应的后验分布。先验和后验的选择满足共轭，这些分布都是指数簇分布的例子。
   简而言之，假设参数$\theta$也是变量而非常量，而且在做实验前已经服从某个分布，然后现在做新实验去更新这个分布假设。

2. 从二项分布到beta分布

   二项分布的似然函数
   $$L(X=s,Y=f|p)=C_n^s{p}^s(1-p{)}^f$$
   先验分布beta分布
   $$P(p|a,\beta )=\frac{p^{a-1}(1-p{)}^{\beta -1}}{\mathrm{B}(a,\beta )}$$
   计算后验分布
   $$P(X=s,Y=f,p|a,\beta )=\frac{p^{s+a-1}(1-p{)}^{f+\beta -1}}{\mathrm{B}(s+a,f+\beta )}$$

3. 多项分布到Dirichlet分布

   同上可以证明多项分布与Dirichlet分布共轭

马尔科夫蒙特卡洛

一、 Inverse CDF

• cdf(累计分布函数)

$$F(x)={\int }_{-\infty }^{x}f(x)dx$$

高斯的CDF图形

• 采样

1. 求F(x)的反函数$F^{-1}(y)$,进而进行采样
2. 使用uniform(0,1)获取采样点s，进而获取简单计算$$t=F^{-1}(s)$$
3. 上式计算结果极为采样点

• 证明

1. 均匀分布的CDF函数

$$P(x\le a)=H(x)=x(0\le x\le 1)$$

2. 采样有以下性值

$$P(x\le s)=P(x\le F(t))=F(t)$$

• 总结

  对概率密度函数$f$进行采样可以使用以上方式进行，但是并非所有的CDF都容易求得或其逆容易求得因此使用了其它方法

二、 Reject Sampling

• 采样类比

1. 目标分布$\pi (x)$，分布$q(x)$和常数$M$，通过对$q(x)$的采样实现对$\pi (x)$采样，满足：

   $q(x)$采样比较容易
   $q(x)$的形状接近$\pi (x)$，且$\forall x,\pi (x)\le Mq(x)$,即保证$0\le \frac{\pi (x)}{Mq(x)}\le 1$

• 采样过程

1. 生成样本$x\backsim q(x)$和 $u\backsim Uniform[0,1]$
2. 若$$u\le \frac{\pi (x)}{Mq(x)}$$则接受样本x
3. 则接受样本服从$\pi (x)$分布

• 证明

1. 等价于

   产生样本$X\backsim q(X)$和$U\backsim [0,1]$
   $Y=Mq(X)U$，若$Y\le \pi (X)$，则接受X

2. x的概率密度如下

   $$p_x(x)=q(x)$$

3. y的概率密度

   $$F(y|x)=P(Y\le y|x)=P(Mq(x)U\le y|x)=P(U\le \frac{y}{Mq(x)}|x)$$

   上式表示在X发生的情况下y发生的情况$$P(U\le \frac{y}{Mq(x)})=\frac{y}{Mq(x)}$$
   得到其概率密度函数如下：
   $$p_y(y|x)=\frac{1}{Mq(x)}$$

4. 联合密度函数

   $$p(x,y)=p_x(x)p_y(y|x).=\frac{1}{M}$$

5. 按接受-拒绝采样抽出的随机数d的概率

   $$F(d|accept)=P(X\le d|Y\le \pi (x))=\frac{P(X\le d,Y\le \pi (x))}{P(Y\le \pi (x))}={\int }_{-\infty }^d\pi (x)dx$$

• 缺点

  选择q(x)非常重要，当$q(x)$与$\pi (x)$相差较大时采样效率就会非常低

三、蒙特卡洛采样

• 细致平稳条件

  $$\pi (x^{\ast })K(x^{\ast }\to x)=p(x)K(x\to x^{\ast })$$

• 使用的过程

  以一维分布为例
  initialise $x^0$
  for i =0 to N-1
  u ~ U(0,1)
  $x^{\ast }\backsim q(x^{\ast }|x^i)$
  $ifu<a(x^{\ast })=min(1,\frac{\pi (x^{\ast })q(x|x^{\ast })}{\pi (x)q(x^{\ast }|x)})x^{i+1}=x^{\ast }$
  $else{x}^{i+1}=x^i$

• 证明其满足detail balance

  需要证明：$\pi (x)K(x\to x^{\ast })=\pi (x^{\ast })K(x^{\ast }\to x)$
  $$K(x\to x^{\ast })=q_{(}{x}^{\ast }|x)min(1,\frac{\pi (x^{\ast })q(x^{\ast }|x)}{\pi (x)q(x^{\ast }|x)})$$

  原式转化为
  $$\pi (x)K(x\to x^{\ast })=\pi (x)q(x^{\ast }|x)min(1,\frac{\pi (x^{\ast })q(x^{\ast }|x)}{\pi (x)q(x^{\ast }|x)})$$
  $$=min(\pi (x)q(x^{\ast }|x),\pi (x^{\ast })q(x^{\ast }|x))$$
  $$=\pi (x^{\ast })q(x^{\ast }|x)min(1,\frac{\pi (x)q(x^{\ast }|x)}{\pi (x^{\ast })q(x|x^{\ast })})$$
  $$=\pi (x^{\ast })K(x^{\ast }\to x)$$

四、Gibbs Sampling

• 过程

  已知 $x^1,y^1,z^1$
  $$x^2\backsim P(x|y^1,z^1)$$
  $$y^2\backsim P(y|x^2,z^1)$$
  $$z^2\backsim P(z|x^2,y^2)$$
  $$x^3\backsim P(z|x^2,y^2)$$

• 证明Gibbis 与 蒙特卡洛关系

1. 当采样第i个样本时

$$\pi (x_i^{\ast }|X_{-i})=q_i(x^{\ast }|x)$$

• 需证明

$$\pi (x^{\ast })q_i(x|x^{\ast })=\pi (x^{\ast })q_i(x|x^{\ast })$$

• 对应的接收率为

$$\frac{\pi (x^{\ast })q(x|x^{\ast })}{\pi (x)q(x^{\ast }|x)}=\frac{\pi (x^{\ast })\pi (x_i|X_{-i}^{\ast })}{\pi (x)\pi (x_i^{\ast }|X_{-i})}$$

• 采样时$X_{-i}^{\ast }=X_{-i}$因此有以下公式
  $$\frac{\pi (x_i^{\ast }|X_{-i}^{\ast })\pi (x_i|X_{-i}^{\ast })}{\pi (x_i|X_{-i})\pi (x_i^{\ast }|X_{-i})}=1$$

• 总结

  吉布斯采样可以直接在$\pi (x_i|X_{-i})$上依次进行采样

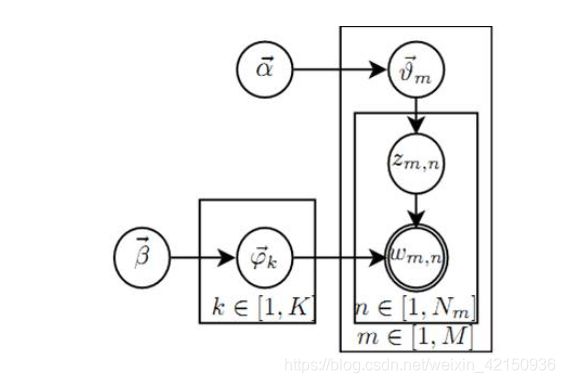
主题模型

• LDA

  1. LDA是一种无监督的贝叶斯模型
  2. 是一种主题模型，它可以将文档集中的每篇文档的主题按照概率分布的形式给出。同时它是一种无监督学习算法，在训练时不需要手工标注的训练集，需要的仅仅是文档集以及指定主题的数量K即可。此外LDA的另一个优点则是，对于每个主题均可找出一些词语来描述它。
  3. 是一种典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的顺序，一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

• 生成词过程

  例：

  
  

  1. $a\to {\theta }_m\to z_{m,n}$,这个过程表示在生成m篇文档时，先抽取一个doc-topic骰子${\theta }_m$,然后投掷这个筛子生成文档第n个词topic编号$z_{m,n}$r
  2. $\beta \to {\phi }_k\to w_{m,n}$,这个过程表示如下动作生成第m篇文档中的第n个词：在K个topic-word筛子${\phi }_k$中,选择编号为$k=z_{m,n}$这个筛子进行投掷，生成单词$w_{m,n}$

• LDA模型理解

  LDA生成模型中，M篇文档会对应于M个独立的Dirchlet-Multionmial共轭分布。K个主题会生成K个独立的Dirichlet-Multionmial共轭结构。下面将分析LDA是如何被分解为M+K个Dirichlet-Multionmial共轭结构

1. 第一个物理过程

   此过程主要时需要获取${\theta }_m$,我们知道$P({\theta }_m|z_m,a)\propto P({\theta }_m|a)P(z_m|{\theta }_m)$因此我们可以对后面的数据进行优化，操作如下：
   $$P(z_m|a)={\int }_{{\theta }_m}P(z_m|{\theta }_m)P({\theta }_m|a)d_{{\theta }_m}=\frac{\Delta (n_m+a)}{\Delta (a)}$$
   同时${\theta }_m\backsim Dir({\theta }_m|n_m+a)$且对整个词库而言满足以下公式：
   $$P(z|\alpha )=\prod _{m=1}^{M}P(z_m|\alpha )=\prod _{m=1}^M\frac{\Delta (n_m+a)}{\Delta (a)}$$
   注：$n_m$表示第m个文档中对应主题所形成的分布，即$[n_1,n_2,\cdots ,n_k{]}_m$

2. 第二个物理过程

   此过程主要获取${\phi }_k$,我们知道$P({\phi }_k|w_{(k)},\beta )\propto P({\phi }_k|\beta )P(w_{(k)}|{\phi }_k)$,因此我们需要对后面的数据进行优化，操作如下：
   $$P(w_{(k)}|\beta )=\frac{\Delta (n_k+\beta )}{\Delta (\beta )}$$
   同时${\phi }_k\backsim Dir({\phi }_k|n_k+\beta )$对整个语料而言：
   $$P(w|z,\beta )=\prod _{k=1}^K\frac{\Delta (n_k+\beta )}{\Delta (\beta )}$$
   注：$n_k$表示第k个主题中word形成的分布，即$[n_1,n_2,\cdots ,n_N{]}_k$

3. 综合有整个词库中主题、词的联合分布如下：

   $$P(w,z|\alpha ,\beta )=\prod _{k=1}^K\frac{\Delta (n_k+\beta )}{\Delta (\beta )}\prod _{m=1}^M\frac{\Delta (n_m+a)}{\Delta (a)}$$

• 使用Gibbs Sampling法求解$P(z|w)$

  Gibbs采样需要进行用到$P(z_i=k,w_i=t|z_{-i},w_{-i})$,因此需要以下推导：

  有了联合分布$p(w,z)$，则Gibbs Sampling就可以发挥作用了,语料库$z$中的第i个词对应的topic我们记为$z_i$，其中$i=(m,n)$表示第m个文本的第n个词，其采样的分布如下：
  $$P(z_i=k,w_i=t|z_{-i},w_{-i})$$
  由于$z_i=k,w_i=t$只涉及到第m篇文档第k个topic，所以只会涉及到两个Dirichlet-Multinomial共轭结构：

  1. $a\to {\theta }_m\to z_m$
  2. $\beta \to {\phi }_k\to w_{(k)}$

• 减少了词的后验分布变为如下公式：

$$P({\theta }_m|z_{-i},w_{-i})=Dir({\theta }_m|n_{m,-i}+\alpha )$$
$$P({\phi }_k|z_{-i},w_{-i})=Dir({\phi }_k|n_{k,-i}+\beta )$$

• 则可以推导出：
  $$P(z_i=k|z_{-i},w)\propto \int p(z_i=k,w_i=t,{\theta }_m,{\phi }_k|z_{-i},w_{-i})d_{{\theta }_m}{d}_{{\phi }_k}=\frac{n_{m,-i}^k+a_k}{{\sum }_{k=1}^K(n_{m,-i}^k+a_k)}\frac{n_{k,-i}^t+{\beta }_t}{{\sum }_{t-1}^V(n_{k,-i}^t+{\beta }_t)}$$

• 采样过程

  我们的目标如下：

  1. 估计模型中的参数${\phi }_1,\cdots ,{\phi }_K$和${\theta }_1,\cdots ,{\theta }_M$
  2. 对于新来的一篇文档d_{new},我们能够计算这篇文档的topic分布${\theta }_{new}$

• 第一步需要训练LDA以估计参数${\phi }_1,\cdots ,{\phi }_K$和${\theta }_1,\cdots ,{\theta }_M$

  1. 随机初始化：对语料中每篇文档中的每个词$w$，随机的赋一个topci编号为$z$
  2. 重新扫描语料库，对每个词w,按照Gibbs Sampling公式重新采样它的topic，在语料库中重新更新；
  3. 重复以上语料库的重新采样过程直到Gibbs Sampling收敛
  4. 统计语料库的topic-word共现频率矩阵，该矩阵就是LDA的模型了

• 第二步为估计新文档的topic分布，此时我们认为Gibbs Sampling公式中的${\hat{\phi }}_{kt}$部分时稳定不变的，是由训练语料得到的模型提供的，所以采样过程中我们只需要估计该文档的topic部分的${\theta }_{new}$

  1. 随机初始化：对当前文档中的每个词w,随机的赋值一个topic编号z
  2. 重新扫描当前文档，按照Gibbs Sampling公式，对每个词w,重新采样它的topic
  3. 重复以上过程直到Gibbs Sampling收敛
  4. 统计文档中的topic分布，该分配就是${\theta }_{new}$

• 使用sklearn实现一个LDA算法

1. 获取数据

    from sklearn.datasets import fetch_20newsgroups
    dataset = fetch_20newsgroups(shuffle=True,random_state=1,remove=('headers','footers','quotes'))
    n_samples = 2000
    data_samples = dataset.data[:n_samples]
   

2. 文本处理

    import nltk
    import string
    from nltk.corpus import stopwords
    from nltk.stem.porter import PorterStemmer
   
    def textPrecessing(text):
        #小写
        text = text.lower()
        #去除特殊标点
        for c in string.punctuation:
            text = text.replace(c,' ')
        #分词
        wordList = nltk.word_tokenize(text)
        #去除停用词
        filtered = [w for w in wordList if w not in stopwords.words('english')]
        #保留名词与特定POS
        refiltered = nltk.pos_tag(filtered)
        filtered = [w for w,pos in refiltered if pos.startswith('NN')]
        #词干化
        ps = PorterStemmer()
        filtered = [ps.stem(w) for w in filtered]
        return ' '.join(filtered)
   
    docLst = []
    for desc in data_samples:
        docLst.append(textPrecessing(desc))
   

3. 将数据存入文档

    with open('./data.txt','w') as f:
        for line in docLst:
            f.write(line+'\n')
   

4. 词频统计

    from sklearn.feature_extraction.text import CountVectorizer
    from sklearn.externals import joblib
    tf_vectorizer = CountVectorizer(max_df=0.95,min_df=2,max_features=500,stop_words='english')
    tf = tf_vectorizer.fit_transform(docLst)
    joblib.dump(tf_vectorizer,'.\model.pck')
   

5. LDA训练

    from sklearn.decomposition import LatentDirichletAllocation
    n_topics = 30
    lda = LatentDirichletAllocation(n_topics=n_topics,max_iter=50,learning_method='batch')
    lda.fit(tf)
   

6. 结果展示

   def print_top_words(model,feature_names,n_top_words):
       for topic_idx,topic in enumerate(model.components_):
           print('Topic #%d'%topic_idx)
           print(' '.join([feature_names[i] for i in topic.argsort()[: -n_top_words -1:-1]]))
           
       print(model.components_)
   
   n_top_words=20
   tf_feature_names = tf_vectorizer.get_feature_names()
   print_top_words(lda,tf_feature_names,n_top_words)