【MATLAB】用地图表白:绘制Bonne投影下的世界地图
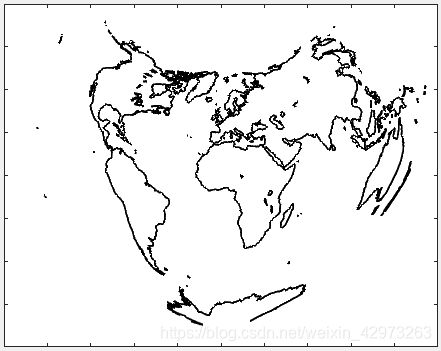
昨天是情人节(本来是昨天写的,发出来已经零点之后了). 我们用世界地图来表白. 先放出最后成果:
那我们就来看一下用MATLAB绘制Bonne投影下绘制世界地图的方法.
基本思路
利用所谓“矢量数据结构”. 地球表面上任何一点都有一组经纬坐标与之对应. 对于世界海岸线,从中选取若干个点,获取它们的经纬坐标,再对这些坐标作地图投影变换,把变换后的点画在纸(或者电脑屏幕)上,依次连接起来,最后添加经纬线、对地图做些修饰就完成了.
具体实现步骤如下:
Step1: 加载世界海岸线数据
MATLAB的地图工具箱中预置了世界海岸线数据,只要load一下就可以了:
load coast
在工作区中看到了名为【lat】和【long】的两个长度为9865的向量:
这就是前面提到的“若干个点”的经纬坐标,单位是“度”,负值表示“西经”或“南纬”,正值表示“东经”或“北纬”.
拿到世界海岸线数据后非常高兴,迫不及待地想画出来试试,于是plot一下看看效果:
plot(long, lat)
就能得到:

已经有了世界地图的样子. 这里对原始经纬坐标“没有作任何变换”,实际上是画出了【等距圆柱投影】下的世界地图.
现在我们仔细观察一下刚才画的地图,画出东经180°经线(图中红线):
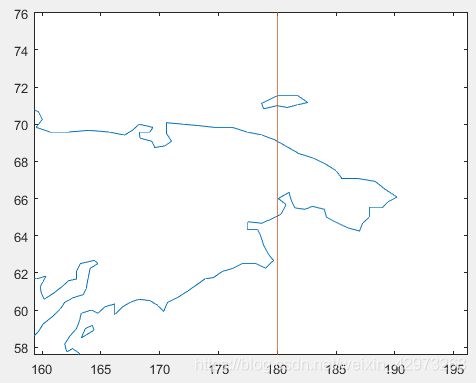
发现俄罗斯远东地区延伸到180°经线以东去了. 从经度向量中提取大于180的值:
boole = long > 180;
fareast = long(boole)
可以看到43个满足要求的数值,原始数据确实如此.
直接使用地图工具箱中自带的海岸线数据未尝不可,(至少保证了大陆的完整性);但我们想到最后成图中出来的这小点不太美观,考虑把经度大于180的数值转成西经.
如果直接:
arr = find(boole);
for i = arr
long(i) = long(i) – 360;
end
就会得到意想不到的结果(其实也能想到会发生什么):
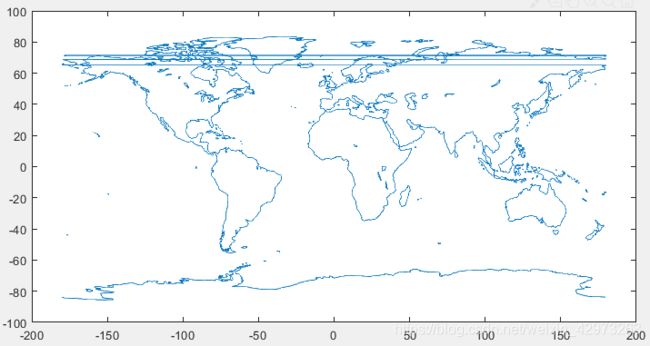
这样做将导致原本跨越180°经线两侧的相邻点位于整张图的左右两侧(且仍相邻),最后将各点依次连线时就直接从左连到右……
换个办法. 在跨越180°经线的两相邻点之间分别插入±180,并在±180之间插入NaN,连线连到NaN处中断(对纬度也作类似操作,插入点的纬度取两边的加权平均值),就没有问题了:
i = 1; len = length(long);
while i < len
if long(i) <= 180 & long(i + 1) > 180
lat0 = (lat(i) * (long(i + 1) - 180) + lat(i + 1) * (180 - long(i))) / (long(i + 1) - long(i));
for j = len:-1:(i + 1)
long(j + 3) = long(j); lat(j + 3) = lat(j);
end
long(i + 2) = NaN; lat(i + 2) = NaN;
long(i + 1) = 180; lat(i + 1) = lat0;
long(i + 3) = -180; lat(i + 3) = lat0;
len = len + 3; i = i + 3;
else if long(i) > 180 & long(i + 1) <= 180
lat0 = (lat(i) * (long(i + 1) - 180) + lat(i + 1) * (180 - long(i))) / (long(i + 1) - long(i));
for j = len:-1:(i + 1)
long(j + 3) = long(j); lat(j + 3) = lat(j);
end
long(i + 2) = NaN; lat(i + 2) = NaN;
long(i + 1) = -180; lat(i + 1) = lat0;
long(i + 3) = 180; lat(i + 3) = lat0;
len = len + 3; i = i + 3;
end
end
i = i + 1;
end
for i = 1:len
if long(i) > 180
long(i) = long(i) - 360;
end
end
再画图看一下(其中红线为东西180°经线,问题解决):
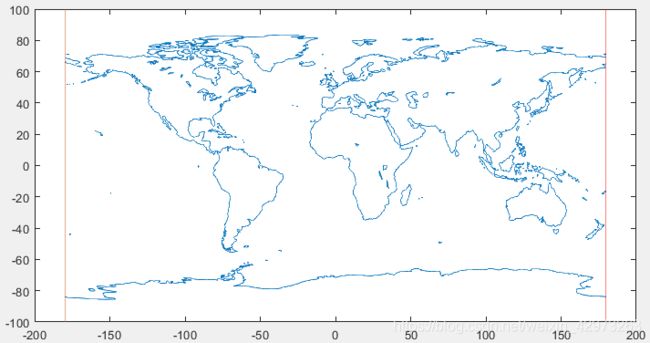
这里得到的长度为9877的新向量【lat】和【long】是我们想要的,并且以后可能也会使用,不妨保存一下便于今后直接读取:
save coast1 long lat
这样第一步操作就完成了.
Step2: 根据投影公式对海岸线数据作变换,并画出图形
实际上MATLAB的地图工具箱中预设了很多种投影方法(当然包括今天要画的Bonne投影),执行以下操作,貌似今天的任务就完成了(并且还给陆地区域上了绿色):
load coast
axesm bonne
patchm(lat, long, ‘g’)
运行一下,就是这样:
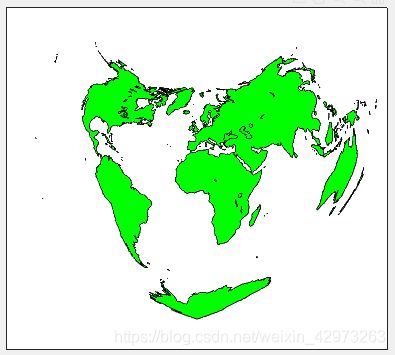
直接用别人预置好的函数画图没什么意思,我们还是来看一下Bonne投影的投影公式:1
Bonne投影是一类【等积伪圆锥投影】(非地学类专业,搞太不懂的就直接忽略这一段). 记(正轴)圆锥面与地球面的切线(标准纬线)的纬度为 φ 0 \varphi_0 φ0,规定以下条件:
- 中央经线投影后为直线,且无长度变形;
- 纬线投影为同心圆圆弧,且无长度变形;
- 中央经线与所有纬线正交,标准纬线与所有经线正交;
- 投影前后无面积变形.
略去数学推导,得到地球面上某点 ( λ , φ ) (\lambda, \varphi) (λ,φ)到平面极坐标中某点 ( ρ , θ ) (\rho, \theta) (ρ,θ)的投影公式为:
{ ρ = R cot φ 0 + R φ 0 − R φ θ = R cos φ ρ λ \left\{ \begin{aligned} \rho&=R\cot \varphi_0+R\varphi_0-R\varphi\\ \theta&=\frac {R\cos\varphi}\rho \lambda \end{aligned} \right. ⎩⎪⎨⎪⎧ρθ=Rcotφ0+Rφ0−Rφ=ρRcosφλ
其中 λ \lambda λ是地球面上某点的经度, φ \varphi φ是纬度, R R R是地球半径.
取标准纬线为北纬30°,即 φ 0 = π / 6 \,\varphi_0={\rm \pi}/6 φ0=π/6:
取比例尺为 1 / R 1/R 1/R,这样投影公式中的 R R R均被1取代. 先把刚才的海岸线数据转成弧度制,再按投影公式作变换:
phi0 = pi / 6;
long = long * pi / 180;
lat = lat * pi / 180;
rho = cot(phi0) + phi0 - lat;
theta = cos(lat) .* long ./ rho;
在极坐标下,如果直接polar一下就会得到如下结果:
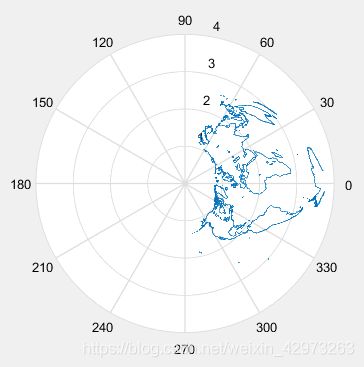
这告诉我们两件事:① 需要把 θ \,\theta\, θ值全部减90°转到我们看着舒服的角度(当然最后再去转图片也行);② polar函数中的极坐标网格不是我们想要的(并且polar函数实际上是在直角坐标下画了一些圆,让我们看起来像一个极坐标网格).
所以,减90°且转成直角坐标:
theta = theta - pi / 2;
x = rho .* cos(theta);
y = rho .* sin(theta);
plot出来(同时设置一下颜色和线宽),就是这样:
plot(x, y, 'k', 'LineWidth', 1.5);
Step3: 添加经纬线
与绘制海岸线轮廓的思路类似,还用“在地球面上选取若干点,作投影变换再依次连线”的方法.
以15°为间隔画纬线:
hold on
latln = -pi/2:pi/12:pi/2;
longln = -pi:0.01:pi;
for i = latln
rho1 = longln * 0 + cot(phi0) + phi0 - i;
delta1 = cos(i) * longln ./ rho1 - pi / 2;
x1 = rho1 .* cos(delta1);
y1 = rho1 .* sin(delta1);
plot(x1, y1, ':', 'color', [0.5, 0.5, 0.5]);
end
以15°为间隔画经线:
longln = -pi:pi/12:pi;
latln = -pi/2:0.01:pi/2;
for i = longln
rho1 = cot(phi0) + phi0 - latln;
delta1 = cos(latln) * i ./ rho1 - pi / 2;
x1 = rho1 .* cos(delta1);
plot(x1, y1, ':', 'color', [0.5, 0.5, 0.5]);
end
对地图作简要修改,就得到成品啦~
支线:用Excel画世界地图
把刚才搞到的经纬度坐标存入.xls文件,用Excel打开,利用【散点图】功能,就能用Excel画世界地图了. 做法如下:
load coast1 % coast1即是刚才保存的.mat格式数据
% 当然如果想直接用他自带的那个远东地区大于180°的,直接load coast就行
mat = [long, lat];
xlswrite(‘coast.xlsx’, mat)
然后打开当前目录下的【coast.xlsx】文件,选择相应数据,插入散点图即得:
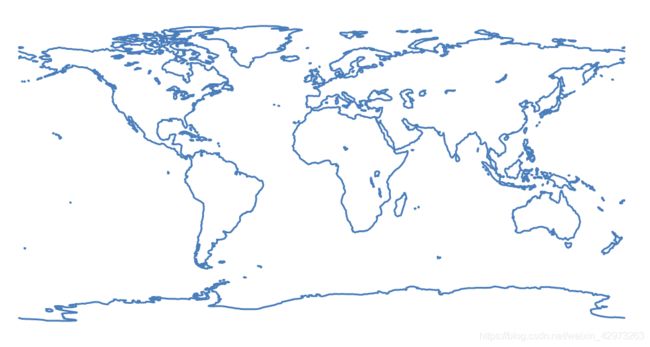
是【等距圆柱投影】下的世界地图. 用Excel中的函数功能也能画出多种投影下的地图,大家不妨尝试一下.
孙达,蒲英霞. 地图投影(第二版)[M]. 南京:南京大学出版社,2012:120~121 ↩︎