通俗理解卡尔曼滤波器原理及matlab中实现

写在最前
在B站上看到一个视频，讲解的非常好，可以快速理解卡尔曼滤波器原理，视频网址，我将视频里面讲解的内容整理了下来，加深自己的理解，同时也希望能帮助他人理解。建议大家去看视频。

卡尔曼滤波器
又叫最佳线性滤波器，有很多好处，比如说：实现简单，是一个纯时域的滤波器，不需要进行频域变换，所以在工程上有很多应用。

第一个公式
假设有一辆小汽车在路上行驶，用位置p和速度v来表示当前的状态–矩阵形式x，另外驾驶员也可以踩刹车或者踩油门，u为向前或向后的加速度，u表示汽车的控制量，如果没有踩油门，也没有踩刹车，那么u=0，小汽车就做匀速直线运动。

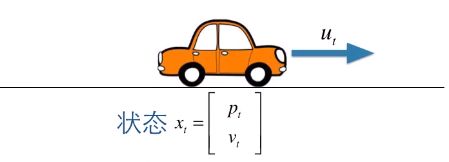
如果已知上一个时刻t-1的状态，那么t时刻的位置和速度就是

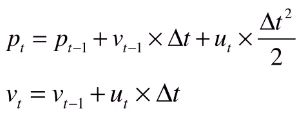
我们观察这两个公式，会发现输出变量是两个输入变量的线性组合。
这就是为什么卡尔曼滤波器是最佳的线性滤波器，因为它只能描述状态与状态之间的线性关系，既然是线性关系，就可以写成矩阵的形式。进一步将两个状态变换矩阵提取出来，最终简化为

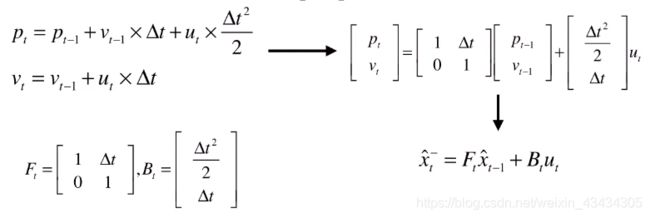
第一个公式：状态预测公式

F是状态转移矩阵，表示从上时刻推测当前状态，B是控制矩阵，表示控制量u如何作用当前时态。^表示估计量，通过观测来尽可能的估计x的值。

第二个公式
有了状态预测公式，就可以推测当前的状态，所有的推测都是包含噪声的，噪声越大，表示推测的偏差也越大。用协方差矩阵来表示。什么是协方差矩阵呢？

先用一维来解释。
假设一维的包含噪声的数据，每次测量的值都不同，但都是围绕在一个中心值的周围，那么表示分布状况最简单的方法是记下中心值和方差。这是假设了一个高斯的分布。

二维的情况
一个二维包含噪声的数据，分别对两个坐标轴投影，在两个轴上都是高斯分布。
那表示它的分布的时候，那么是不是分别记录下来两个高斯分布的中心值和方差就可以了呢？如果两个维度的噪声是独立的，可以这样表示。如果两个维度有相关性，比如，如果一个维度增大了，另一个维度也增大了，也是高斯分布。或者一个维度增大了，另一个维度却减少了，但仍然是高斯分布。

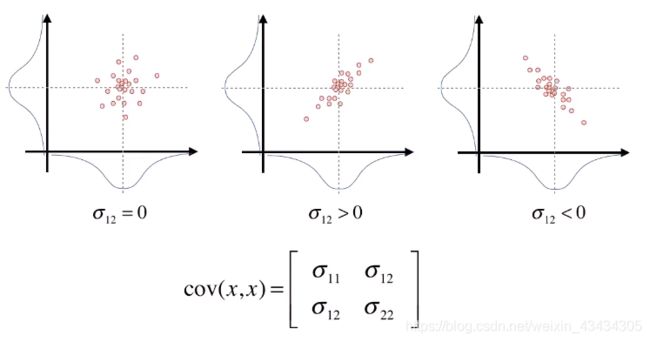
为了表示维度的相关性，除了要记录两个维度的方差，还需要计算它的协方差。
在卡尔曼滤波器中，所有关于不确定性都需要用到协方差矩阵。协方差矩阵用P表示。如何让这种不确定性在每个状态之间传递呢？
需要乘以状态转移矩阵F，至于为什么要乘以两边，这是协方差的性质。

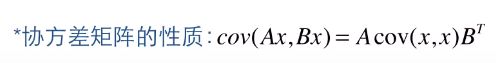
这时候，还需要考虑一件事情，就是我们的预测模型并不是百分百准确，也是包含噪声的。
第二个公式：不确定性在两个状态之间的传递

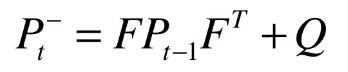
第三个公式
假设我们在公路一边放置了一个激光测距仪，每个时刻可以观察到小汽车的位置，观测的值记为z，汽车本身的状态到观测状态有一个变换关系，记为H。当然这种变换关系只能是线性关系。则把H写成矩阵形式，z和x的维度不一定相同。

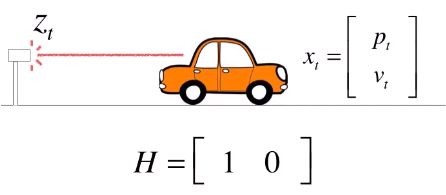
x到z的变换是一种线性变换，H观测矩阵。因为观测也不一定百分百准确，所以加入v为观测值的噪声。这个噪声的协方差矩阵R来表示。由于在这个例子里，观测值是一个一维的值，所以R不是矩阵，是一个单独的值，仅仅表示z的方差。

如果用多种方式来观察小汽车的位置，则z就是一个多维的列向量。包含每一种测量方式的测量值，而每一个测量值都是真实状态的不完全的表现，我们可以从几种不完全的表现中推断出真实的状态，而卡尔曼滤波器数据融合的功能就是在这个观测矩阵中体现出来的。

第三个公式：最佳估计值

后面的括号表示实际的观测值与预测的值之间的残差，K十分关键，它是卡尔曼系数，也叫卡尔曼增益。也是一个矩阵。

第四个公式

卡尔曼增益作用有两方面，一是，权衡预测协方差矩阵和观测协方差的大小，我们是相信预测模型多一点还是相信观测模型多一点，如果是相信预测模型多一点，K就小一点，如果相信观测模型多一点，K就大一点。
二是，把残差的表现形式从观测域转换到状态域。在这个例子里，我们只观察到小汽车的位置，但K里面已经包含了协方差矩阵P的信息，利用位置和速度的相关性，从位置的残差里面推算出了速度的残差，从而可以对状态x的两个维度同时进行修正。

第五个公式
最后一步：噪声协方差矩阵的更新

更新最佳估计值的噪声分布，留给下一步迭代时来用，在这步里，状态的不确定是减小的，而下一步由于噪声的引入，不确定性又会变大，卡尔曼滤波器就是在这种不确定性的变化中寻求一种平衡。

五个公式：

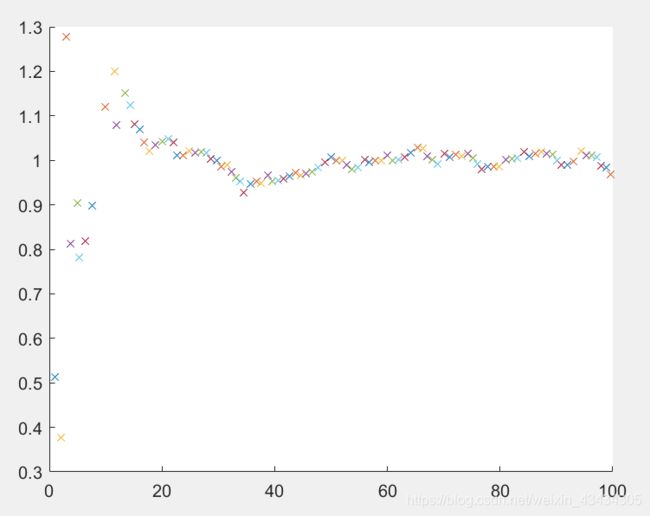
如何在matlab中实现一个卡尔曼滤波器？就上面小车的例子，我们来实现一下：

Z=(1:100);          %观测值
noise=randn(1,100); %方差为1的高斯噪声
Z=Z+noise;          

X=[0;0];            %状态
P=[1 0;0 1];        %状态协方差矩阵
F=[1 1;0 1];        %状态转移矩阵
Q=[0.0001 0;0 0.0001];  %状态转移协方差矩阵
H=[1 0];                %观测矩阵
R=1;                    %观测噪声方差

figure;
hold on;

for i=1:100
    X_=F*X;
    P_=F*P*F'+Q;
    K=P_*H'/(H*P_*H'+R);
    X=X_+K*(Z(i)-H*X_);
    P=(eye(2)-K*H)*P_;
    
    plot(X(1),X(2),'x');    %画点，横轴表示位置，纵轴表示速度
end

最后结果
最后我们可以看到，迭代很少的次数，就达到了稳定状态。因为我们没有添加控制量，所以小车做匀速直线运动。