数学建模算法：Dijkstra（迪杰斯特拉）算法解决你的选择困难症

是否曾经深陷选择困难症，面对一堆选择而无从是从？

一文学会Dijkstra算法解决你的选择困难症

我们可以把问题实例化为从图中1到5，怎么走是最短路径？

一：Dijkstra算法概述.
二：Dijkstra算法图解.
三：Dijkstra算法核心：带权邻阶矩阵.
四：Dijkstra算法Matlab代码实现及结果说明.

一：Dijkstra算法概述

问题解释：
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径

解决问题的算法：

迪杰斯特拉算法（Dijkstra算法）
弗洛伊德算法（Floyd算法）
Dijkstra算法是一种标号法：给赋权图的每一个顶点记一个数，称为顶点的标号,通过不断移动源点的位置及挑出所有点到原点最小距离，并实时更新，最终得出一条最短路程

二：Dijkstra算法图解

2.1总体步骤就三步：

1、当到一个时间点时，图上部分的点的最短距离已确定，部分点的最短距离未确定。

2、选一个所有未确定点中离源点最近的点，把他认为成最短距离。

3、再把这个点所有出边遍历一边，更新所有的点。

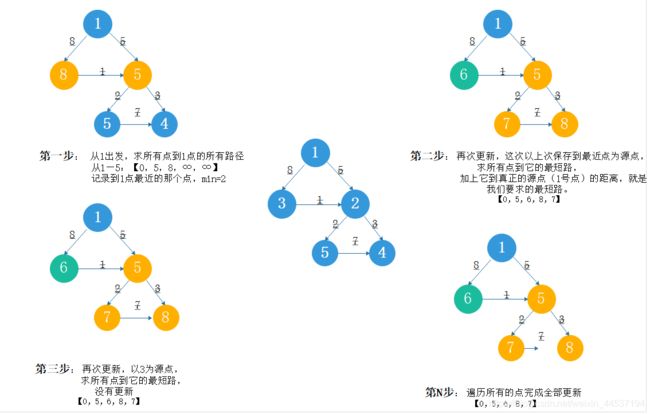
2.2下面手工模拟一下：

（配合插图学习）

以1为源点，求所有点到一号点的最短路径，使用数组保存，初始值都是无穷（∞），原点对本身的距离为0.

先从1号点开始。一号点，map[1][2]=5,一号点离2号点是5，比无穷∞要小，所以dis[2]从无穷大变成了5。顺便，我们用min记录距离1号点最短的点，留着以后会用。

数组变成：dis[0,5,∞,∞,∞]。minn=2。

然后搜到3号点，map[1][3]=8,距离是8，比原来的dis[3]的∞小，于是dis[3]=8。但是8比dis[2]的5要大，所以minn不更新。

数组变成：dis[0,5,8,∞,∞]

接着分别搜索4,5号点，发现map[1][4],map[1][5]都是∞，所以就不更新。

接下来开始：第二次更新。

第二次更新以什么为开始呢？ 就是以上一次我们存下来的，min，相当于把2当源点，求所有点到它的最短路，加上它到真正的源点（1号点）的距离，就是我们要求的最短路。

从2号点开始，搜索3号点，map[2][3]=1，原本dis[3]=8，发现dis[2]+map[2][3]=5+1=6

数组变成：dis[0,5,6,∞,∞] minn=3.

然后搜索4号点，map[2][4]=3,原本dis[4]=∞,所以，dis[2]+map[2][4]=5+3=81,minn不更新。

数组变成：dis[0,5,6,8,∞] ，minn=3.

接着搜索5号点，map[2][5]=2,5+2=7,7<∞,dis[5]=7，minn不变。

数组变成：dis[0,5,6,8,7]

二号点搜完，因为minn是3，继续搜索3号点。

三号点还是按照二号点的方法搜索，发现没有可以更新的，然后搜索四号。

四号搜5号点，发现8+7>5+2,所以依然不更新，然后跳出循环。

现在的估计值就全部为确定值了：

数组变成：dis[0,5,6,8,7]

三：Dijkstra算法核心：带权邻阶矩阵

我们通过一个更加复杂的图论来揭示Dijkstra算法的核心：带权邻阶矩阵

例如此图，我们将所有直接相连的点的距离转化为矩阵:

将此矩阵带入程序，便可得最短路径：

四：Dijkstra算法Matlab代码实现及结果说明

代码如下：

dijkstra.m
function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
   if i~=start
       label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)(label(u)+w(u,v))
            label(v)=(label(u)+w(u,v)); 
         f(v)=u;
         end, 
      end, 
   end   
v1=0;
   k=inf;
   for i=1:n
         ins=0;
         for j=1:length(s)
            if i==s(j)
               ins=1;
            end, 
         end
         if ins==0
            v=i;
            if k>label(v)
               k=label(v);  v1=v;
            end,  
         end,  
   end
   s(length(s)+1)=v1;  
   u=v1;
end
min=label(terminal); path(1)=terminal;
i=1; 
while path(i)~=start
      path(i+1)=f(path(i));
      i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

示例矩阵：

tulun1.m
weight=    [0     2     8     1   Inf   Inf   Inf   Inf   Inf   Inf   Inf;
            2     0     6   Inf     1   Inf   Inf   Inf   Inf   Inf   Inf;
            8     6     0     7     5     1     2   Inf   Inf   Inf   Inf;
            1   Inf     7     0   Inf   Inf     9   Inf   Inf   Inf   Inf;
          Inf     1     5   Inf     0     3   Inf     2     9   Inf   Inf;
          Inf   Inf     1   Inf     3     0     4   Inf     6   Inf   Inf;
          Inf   Inf     2     9   Inf     4     0   Inf     3     1   Inf;
          Inf   Inf   Inf   Inf     2   Inf   Inf     0     7   Inf     9;
          Inf   Inf   Inf   Inf     9     6     3     7     0     1     2;
          Inf   Inf   Inf   Inf   Inf   Inf     1   Inf     1     0     4;
          Inf   Inf   Inf   Inf   Inf   Inf   Inf     9     2     4     0;];
[dis, path]=dijkstra(weight,1, 11)

运行结果如下：