图论算法——Prim算法和Kruskal算法

引言

有关概念可参考博文数据结构之图的概述

我们要学习的第一种计算最小生成树的算法，它每一步都会为一颗生长中的树添加一条边。

下面分析下算法思路

思路

一开始这棵树只有一个顶点，然后会向它添加V-1条边，每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入树中。

Prim算法

每次当我们向(生成)树中添加了一条边之后，也向树中添加了一个顶点。要维护一个包含所有横切边的集合，就要将连接这个顶点和其他所有不在树中的顶点的边加入优先队列。要注意的是，新加入树的顶点与其他已经在树中的顶点的所有边都失效了。
Prim算法的即时实现可以将这样的失效边从优先队列中删掉，我们先来学习延时实现的版本，暂且将这些边留在优先队列中，等要删除它们的时候再检查边的有效性。

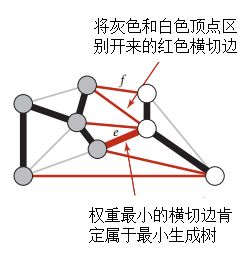
图的一种切分是将图的所有顶点分为两个非空且不重复的集合。这里一个是生成树顶点集合，另一个是待加入生成树的顶点集合。
横切边是一条连接属于两个不同集合的顶点的边。

假设我们要计算下图的最小生成树

延时版本的Prim算法过程如下：

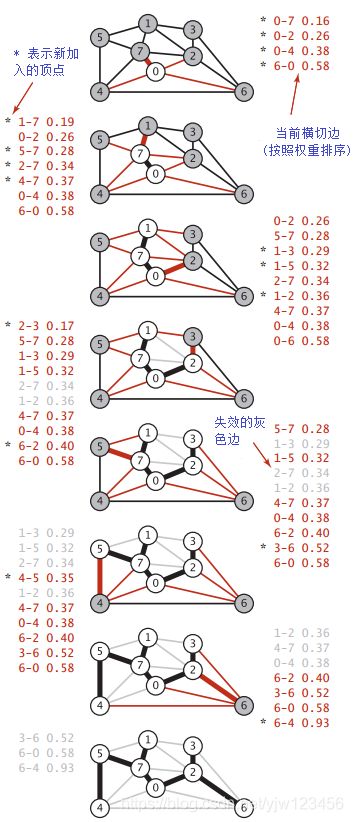
每一张图片都是算法访问过一个顶点之后(被加到生成树中)图和优先队列的状态。
优先队列在图的一侧，新顶点旁边有个*。算法构造最小生成树的过程如下：

• 将顶点0加入最小生成树中，将它邻接的所有边添加到优先队列中。我们可以得到权重最小的边为0-7这条边
• 将顶点7和边0-7加入最小生成树中，此时新加入的邻接边为1-7,5-7,2-7,4-7,继续从优先队列中选出权重最小的边1-7
• 将顶点1和边1-7加入最小生成树中，将该顶点的所有邻接边加入队列，此时队列中权重最小的边为0-2
• 将顶点2和边0-2加入最小生成树中，此时新加入的邻接边为2-3,6-2,选出权重最小的边2-3
• 将顶点3和边2-3加入最小生成树中，此时新加入的邻接边只有3-6，可惜它不是权重最小的边，从队列中选出边5-7
• 将顶点5和边5-7加入最小生成树中，此时新加入的边为4-5,虽然它不是队列中权重最小的边，幸运的是，它前面的边都没资格被选中(它前面的边都属于失效边了，如果增加失效边会形成环)，天命圈选手4-5被选中
• 将顶点4和边4-5加入最小生成树中，得到新的边6-2
• 将顶点6和边6-2加入最小生成树中

在添加了8个顶点和7条边之后，最小生成树就生成了。优先队列中剩下的边都是失效的，可以不去管它们。

延时版本的Prim算法实现

EdgeWeightedGraph的实现见图论算法——加权无向图的数据结构

package com.algorithms.graph;

import com.algorithms.heap.BinaryHeap;
import com.algorithms.heap.Heap;
import com.algorithms.queue.Queue;

/**
 * @author yjw
 * @date 2019/5/24/024
 */
public class LazyPrimMST {
    /**
     * 最小生成树的总权值
     */
    private double weight;
    /**
     * 最小生成树的顶点
     */
    private boolean[] marked;
    /**
     * 最小生成树的边
     */
    private Queue<Edge> mst;

    /**
     * 按照最小权值构造的优先队列
     */
    private Heap<Edge> pq;

    public LazyPrimMST(EdgeWeightedGraph g) {
        pq = new BinaryHeap<>();
        marked = new boolean[g.vertexNum()];
        mst = new Queue<>();
        weight = 0;
        //先访问第一个顶点0
        visit(g,0);
        while (!pq.isEmpty()) {
            //循环跳出条件为pq为空
            //从优先队列中删除并返回权值最小的边
            Edge e = pq.deleteMin();
            //边的两个顶点v和w
            int v = e.either(),w = e.other(v);
            if (marked[v] && marked[w]) {
                //如果该边已经在生成树中，则不执行后面的代码，跳到!pq.isEmpty()判断            
                continue;
            }
            //说明该边不在生成树中，加入最小生成树mst
            mst.enqueue(e);
            weight += e.weight();
            if (!marked[v]) {
                visit(g,v);
            }
            if (!marked[w]) {
                visit(g,w);
            }
        }
    }

    private void visit(EdgeWeightedGraph g,int v) {
        marked[v] = true;
        for (Edge e : g.adj(v)) {
            //将顶点v的所有邻接边加入队列中(除了已经在生成树中的顶点的边)
            if (!marked[e.other(v)]) {
                pq.insert(e);
            }
        }
    }

    /**
     * 返回最小生成树的所有边
     * @return
     */
    public Iterable<Edge> edges() {
        return mst;
    }

    /**
     * 返回总的权重
     * @return
     */
    public double weight() {
        return weight;
    }

    public static void main(String[] args) {
        EdgeWeightedGraph g = new EdgeWeightedGraph(8);
        g.addEdges(0,6,.58,2,.26,4,.38,7,.16);
        g.addEdges(1,3,.29,2,.36,7,.19,5,.32);
        g.addEdges(2,6,.40,7,.34,3,.17);
        g.addEdge(3,6,.52);
        g.addEdges(4,6,.93,7,.37,5,.35);
        g.addEdge(5,7,.28);

        LazyPrimMST lp = new LazyPrimMST(g);
        System.out.println(lp.weight);
        for (Edge e : lp.edges()) {
            System.out.println(e);
        }
    }

}

其中优先队列的实现请访问博文:Java中的优先队列——二叉堆

输出如下：

1.81
0-7(0.16)
1-7(0.19)
0-2(0.26)
2-3(0.17)
5-7(0.28)
4-5(0.35)
2-6(0.40)

运行时间

Prim算法的延时实现计算一幅含有V个顶点和E条边的连通加权无向图的最小生成树所需的空间与E成正比，
所需的时间与$ElogE$成正比(最坏情况)。

Kruskal算法

这种算法实现起来更加简单，主要思想是按照边的权重顺序（从小到大）处理它们，将最小的边加入到最小生成树中（通过小顶堆来实现），当然，新加入的边不能与已加入的边构成环(这一点通过并查集来检查)。直到树中含有V-1条边为止。

Kruskal算法实现

package com.algorithms.graph;

import com.algorithms.UnionFind.QuickFindUF;
import com.algorithms.UnionFind.UF;
import com.algorithms.heap.BinaryHeap;
import com.algorithms.heap.Heap;
import com.algorithms.queue.Queue;

/**
 * @author yjw
 * @date 2019/5/28/028
 */
public class KruskalMST {
    private Queue<Edge> mst;

    private double weight;

    public KruskalMST(EdgeWeightedGraph g) {
        mst = new Queue<>();
        //注意传入的是Iterable
        Heap<Edge> heap = new BinaryHeap<>(g.edges());
        UF uf = new QuickFindUF(g.vertexNum());
        weight = 0.0;
        /**
         * 为什么要小于  vertexNum - 1 ?  因为生成树中最多有vertexNum - 1个边，所以当生成树的边为vertexNum - 1时说明已经生成完毕了
         * 当然还有heap不能为空
         */
        while (!heap.isEmpty() && mst.size() < g.vertexNum() - 1) {
            //取到当前权重最小边
            Edge edge = heap.deleteMin();
            //得到边的两个顶点
            int v = edge.either(),w = edge.other(v);
            //判断是否会形成环，即该边两个顶点是否已经连通
            if (uf.connected(v,w)) {
                continue;
            }
            //不会则加入并查集和最小生成树
            weight += edge.weight();
            uf.union(v,w);
            mst.enqueue(edge);
        }
    }

    public Iterable<Edge> edges() {
        return mst;
    }

    public double weight() {
        return weight;
    }

    public static void main(String[] args) {
        EdgeWeightedGraph g = new EdgeWeightedGraph(8);
        g.addEdges(0,6,.58,2,.26,4,.38,7,.16);
        g.addEdges(1,3,.29,2,.36,7,.19,5,.32);
        g.addEdges(2,6,.40,7,.34,3,.17);
        g.addEdge(3,6,.52);
        g.addEdges(4,6,.93,7,.37,5,.35);
        g.addEdge(5,7,.28);

        KruskalMST km = new KruskalMST(g);
        System.out.println(km.weight());
        for (Edge e : km.edges()) {
            System.out.println(e);
        }
    }
}

输出如下：

1.81
0-7(0.16)
2-3(0.17)
1-7(0.19)
0-2(0.26)
5-7(0.28)
4-5(0.35)
2-6(0.40)

该算法用到了优先队列和并查集

运行时间

Kruskal算法计算一幅含有V个顶点和E条边的连通加权无向图的最小生成树所需的空间与E(边数)成正比，
所需的时间与$ElogE$成正比(最坏情况)。