这篇文章记录我所看的视频课【tensorflow笔记】的代码，这些代码并不是课上讲的代码，而是我自己听了课之后根据自己的想法敲写的，所以不是100%还原老师的代码。
1.前向传播
一个很简单很简单的前向传播例子
import numpy as np
import tensorflow as tf
#生成输入数据
x_data=np.random.rand(100)
y_data=0.2*x_data+0.1
#前向传播
k=0.5
b=0.3
x=tf.placeholder(tf.float32)
y=k*x+b
#初始化
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
print(sess.run(y,feed_dict={x:x_data}))2.反向传播
一个很简单很简单的反向传播的例子
import numpy as np
import tensorflow as tf
#生成输入数据
x_data=np.random.rand(100)
y_data=0.2*x_data+0.1
#前向传播
k=tf.Variable(0.5)
b=tf.Variable(0.3)
y=tf.Variable(0)
y=k*x_data+b
#反向传播
error=y-y_data
loss=tf.reduce_mean(tf.square(error))
optimizer=tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#初始化
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for i in range(200):
sess.run(optimizer)
if i%20==0:
print(sess.run([k,b,loss]))下面也是反向传播，但这个代码比上面那个有难度提升,因为我们开始使用权重矩阵
import numpy as np
import tensorflow as tf
#输入数据
x_data= np.random.rand(32,2)
y_data=[[x1+x2+(rmd.rand()/10.0-0.05)] for (x1,x2) in x_data]
"""这行代码与下句等同
y=[]
for [x1,x2] in x:
y.append([x1+x2+(np.random.rand()/10-0.05)])
"""
#前向传播
x=tf.placeholder(tf.float32,shape=(None,2))
y=tf.placeholder(tf.float32,shape=(None,1))
w1= tf.Variable(tf.random_normal([2, 1]))#正态分布
z= tf.matmul(x, w1)#点积
#反向传播
loss=tf.reduce_mean(tf.square(z-y))
optimizer=tf.train.GradientDescentOptimizer(0.002).minimize(loss)
#初始化
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for i in range(20000):
sess.run(optimizer,feed_dict={x:x_data,y:y_data})
if i%5000==0:
print(f"第{i}次训练结果：")
print(sess.run(w1))
print("最终结果：\n",sess.run(w1))3.损失函数
损失函数很多，你可以自己写，也可以用经典的损失函数（线性回归、sigmoid、softmax）
经典的线性回归上面两个代码我们已经用了，这次写一下自己定义的损失函数：
import tensorflow as tf
w=tf.Variable(5.)
loss=tf.square(w+1)
optimizer=tf.train.GradientDescentOptimizer(0.2).minimize(loss)
inti=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(inti)
for i in range(50):
sess.run(optimizer)
print(sess.run([w,loss]))可以看到，loss是自己定义的函数，而不是经典的三大金刚。loss可以随便定义，你想要的啥就写啥，这里方便理解所以写了个最简单的loss=（w+1）^2，在实际问题中肯定不会这么简单。
4.学习率
这个就不写代码了，就是在使用各种优化器的时候要设定学习率，就是反向传播一次更新的程度大小。
学习率的设置也有讲究，小了更新慢，大了会爆炸，所以我们说一下怎么设置学习率：
在实际编码时，我们通常使用【指数衰减学习率】：
这是指数衰减学习率的公式，你可以不太懂它的含义，只要你会敲代码就可以
代码如下：
globe_step=tf.Variable(0，trainable=False) #计数器，用来记录当前运行了几轮batch_size，该参数不参与训练，所以trainable=False
learning_rate=tf.train.exponential_decay(
LEARNING_RATE_BASE, #学习率初始值
globe_step, #计数器
LEARNING_RATE_STEP, #学习率更新周期，值为总样本数÷batch_size样本数
LEARNING_RATE_DECAY, #学习率衰减率
staircase=True #True表示以不连续的间隔衰减学习速率，最后曲线是锯齿状
False表示以连续的间隔衰减学习速率，最后曲线是光滑状
)
在训练时，要求在tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step)的minimize里写上global_step
实际应用如下：
import tensorflow as tf
#设置learning_rate
global_step=tf.Variable(0，trainable=False)
LEARNING_RATE_BASE=0.1
LEARNING_RATE_STEP=1
LEARNING_RATE_DECAY=0.99
learning_rate=tf.train.exponential_decay(LEARNING_RATE_BASE,global_step,LEARNING_RATE_STEP,LEARNING_RATE_DECAY,staircase=True)
#设置训练数据
w=tf.Variable(5.)
#设置损失函数
loss=tf.square(w+1)
#设置优化器
optimize=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step)
#初始化
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for i in range(40):
sess.run(optimize)
learning_rate_val=sess.run(learning_rate)
global_step_val=sess.run(global_step)
w_val=sess.run(w)
loss_val=sess.run(loss)
print(f"经过{i}步，当前global_step为{ global_step_val}，w为{w_val}，learning_rate为{learning_rate_val}，loss为{loss_val}")一定多多留意独特之处！
5.正则化
我们用正则化来缓解泛化效果差的问题，就是给权重一个矩阵，加在loss上。
如图所示，正则化后的loss，是原来的loss再加上正则化项，正则化项就是正则化参数*loss（w），这个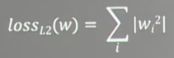
，跟吴恩达讲的一模一样。
正则化项的表示代码为tf.contrib.layers.l2_regularizer（lambda）(w)，其中lambda是正则化参数，w是权重
tf.add_to_collection("losses",tf.contrib.layers.l2_regularizer(lambda)(w)) #把正则化项放入一个名为"losses"的集合器里面，我们打算用这个losses来表示整个正则化项了。
loss=cem+tf.add_n(tf.get_collection("losses")) #cem是原来的loss，现在把正则化项和之前的最原始的loss加在一起，就得到了正则化后的loss
ok，你可能看不懂，问“为什么要这么麻烦？直接把正则化项加进cem不就行了吗？”是的，我也不懂为什么，但就是这样的一环套一环，你还就真得按照这个代码去操作，不然你做不出来。
下面看代码：
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#设置batch（临时样本）
step=30
#产生输入数据
x_data=np.random.randn(300,2)
#产生输入数据集的标签（正确答案）
y_data=[int(x0*x0+x1*x1<2) for (x0,x1) in x_data]
#遍历y_data中的每个元素，1赋值red，其余赋值blue，这样可视化显示时容易区分
y_s=[["red" if y else "blue"] for y in y_data]
#数据变形，按行堆叠成一个新数组
x_data=np.vstack(x_data).reshape(-1,2)#numpy中，shape里写-1，相当于tensorflow里写None
y_data=np.vstack(y_data).reshape(-1,1)
print(x_data)
print(y_data)
print(y_s)
#用plt.scatter画出数据集x_data各行中第0列元素和第一列元素的点即各行的（x0,x1），用各行y_s对应的值表示颜色
plt.scatter(x_data[:,0],x_data[:,1],c=np.squeeze(y_s))
plt.show()
#定义神经网络的输入、参数和输出，定义前向传播
def get_weight(shape,regularizer):
w=tf.Variable(tf.random_normal(shape),dtype=tf.float32)
tf.add_to_collection("losses",tf.contrib.layers.l2_regularizer(regularizer)(w))
return w
def get_bias(shape):
b=tf.Variable(tf.constant(0.01,shape=shape))
return b
#输入层输入
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
#输入层到隐藏层
w1=get_weight([2,11],0.01)
b1=get_bias([11])
y1=tf.nn.relu(tf.matmul(x,w1)+b1)
#隐藏层到输出层
w2=get_weight([11,1],0.01)
b2=get_bias([1])
y=tf.matmul(y1,w2)+b2#输出层不激活（仅限这个代码不激活）
#定义损失函数
loss_mse=tf.reduce_mean(tf.square(y-y_))
loss=loss_mse + tf.add_n(tf.get_collection("losses"))
#定义反向传播
optimizer=tf.train.AdamOptimizer(0.0001).minimize(loss)
#初始化
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for i in range(40000):
start=(i*step)%300
end=start+step
sess.run(optimizer,feed_dict={x:x_data[start:end],y_:y_data[start:end]})
if i%2000==0:
loss_mse_val=sess.run(loss_mse,feed_dict={x:x_data,y_:y_data})
print(f"经过{i}步，loss现为：{loss_mse_val}")
# xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成二维网格坐标点
xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
# 将xx , yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
grid = np.c_[xx.ravel(), yy.ravel()]
# 将网格坐标点喂入神经网络 ，probs为输出
probs = sess.run(y, feed_dict={x: grid})
# probs的shape调整成xx的样子
probs = probs.reshape(xx.shape)
print("w1:\n", sess.run(w1))
print("b1:\n", sess.run(b1))
print("w2:\n", sess.run(w2))
print("b2:\n", sess.run(b2))
plt.scatter(x_data[:, 0], x_data[:, 1], c=np.squeeze(y_s))
plt.contour(xx, yy, probs, levels=[.5])
plt.show()