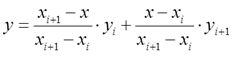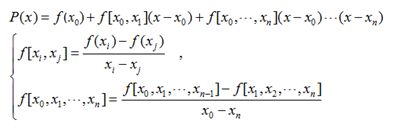插值、拟合和逼近的区别
据维基百科,科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合。通过拟合得到的函数获得未知点的数据的方法,叫做插值。其中,拟合函数经过所有已知点的插值方法,叫做内插。
拟合是已知点列,从整体上靠近它们;插值是已知点列并且完全经过点列;逼近是已知曲线,或者点列,通过逼近使得构造的函数无限靠近它们。
最小二乘意义下的拟合,是要求拟合函数与原始数据的均方误差达到极小,是一种整体意义的逼近,对局部性质没有要求。而所谓"插值",就是要在原有离散数据之间"插入"一些值,这就要求插值函数必须通过所有的离散点,插值函数在离散点之外的那些点都相当于"插入"的值。插值有全局插值,也有局部插值(比如分段线性插值),插值误差通常考虑的是逐点误差或最大模误差,插值的好坏往往通过某些局部的性质来体现,比如龙格现象或吉布斯振荡。
[知乎 拟合与插值的区别?]
插值方法
多项式插值
对于大部分多项式插值函数,插值点的高度值可以视为所有(或某些)节点高度值的线性组合,而线性组合的系数一般是x坐标的多项式函数,称作基函数。对于一个节点的基函数,它在x等于该节点的x时等于1,在x等于其他节点的x时等于0。这就保证曲线必定经过所有节点,所以属于内插方法。
在本小节,均以一组随机数作为已知的高度值,使它们对应于间隔固定的x坐标,使用不同的插值函数获得各已知点(称为插值函数的节点)之外其它x坐标所对应的高度值,画出这些点所对应的曲线。再把所有高度值转换成灰度值,以颜色的变化比较各插值函数。
原点列如图:(假定横向为x,纵向为y。各点x坐标的间隔是固定的,但y坐标是随机的)
线性插值
线性插值是用一系列首尾相连的线段依次连接相邻各点,每条线段内的点的高度作为插值获得的高度值。
以(xi,yi)表示某条线段的前一个端点,(x(i+1),y(i+1))表示该线段的后一个端点,则对于在[xi,x(i+1)]范围内的横坐标为x的点,其高度y为:
为便于与后面各函数比较,写成比较对称的形式:
其中,yi和y(i+1)的两个参数称为基函数,二者之和为1,分别代表yi和y(i+1)对插值点高度的权值。
[wikipedia线性插值]
插值图像如下:
将高度转化为灰度,得到如下条带:
线性插值的特点是计算简便,但光滑性很差。如果用线性插值拟合一条光滑曲线,对每一段线段,原曲线在该段内二阶导数绝对值的最大值越大,拟合的误差越大。
二次插值
如果按照线性插值的形式,以每3个相邻点做插值,就得到了二次插值:
OpenGL实现代码如下:
- void quadratic(float p[20][2])
- {
- float x,y;
- int i;
- float x01,x02,x12;
- glColor3f(0.0,0.0,1.0);
- glBegin(GL_LINE_STRIP);
- for(i=0;i<20;i+=2)
- {
- x01=p[i][0]-p[i+1][0];
- x02=p[i][0]-p[i+2][0];
- x12=p[i+1][0]-p[i+2][0];
- for(x=p[i][0];x<=p[i+2][0];x+=1.0)
- {
- y=(x-p[i+1][0])*(x-p[i+2][0])/x01/x02*p[i][1]-(x-p[i][0])*(x-p[i+2][0])/x01/x12*p[i+1][1]+(x-p[i][0])*(x-p[i+1][0])/x02/x12*p[i+2][1];
- glVertex2f(x,y);
- }
- }
- glEnd();
-
}
二次(分段)插值图像如下:
转换成灰度值如图:
二次插值在每段二次曲线内是光滑的,但在每条曲线的连接处其光滑性可能甚至比线性插值还差。二次插值只适合3个节点的情形,当节点数超过3个时,就需要分段插值了。
Cubic插值
如果想要保证各段曲线连接处光滑(一阶导数相同),并且不想使用除法运算,可以考虑Cubic插值函数:
其中,v代表插值点,v0、v1、v2、v3代表4个连续的节点。t取值为[0,1],将会产生一段连接v1和v2的曲线。也就是说,如果有n个节点,Cubic插值函数将会产生(n-2)段曲线,位于首尾两端的节点不会纳入曲线。
实现代码如下:
- float cubic(float v0,float v1,float v2,float v3,float x)
- {
- float v32=v3-v2;
- float v01=v0-v1;
- float v20=v2-v0;
- float temp=(v32-v01)*x;
- temp=(temp+v01+v01-v32)*x;
- temp=(temp+v20)*x+v1;
- return temp;
- }
- void drawCubic(float p[20])
- {
- float x,y;
- int step;
- float delta;
- glColor3f(0.0,0.0,1.0);
- glBegin(GL_LINE_STRIP);
- for(step=0;step<17;step++)
- {
- for(delta=0.0;delta<=1.0;delta+=0.05)
- {
- x=delta*(p[step+1][0]-p[step][0])+p[step][0];
- y=cubic(p[step],p[step+1],p[step+2],p[step+3],delta);
- glVertex2f(x,y);
- }
- }
- glEnd();
-
}
Cuibc插值图像如下:
转化成灰度如图:
Cubic插值可以产生整体上光滑的曲线,但容易产生较剧烈的波动,使得曲线的最高点比最高的节点还高、曲线的最低点比最低的节点还低。所以对颜色等取值有严格的上下界的数据进行插值时,会造成曲线的截取,破坏其光滑性。比如颜色(RGB三个分量取值范围都是[0,255]),如果最高的节点是255,最低的节点是0,那么插值后负数会被截取成0,大于255的数会被截取成255。
拉格朗日多项式插值
解决插值函数的直接构造问题以及插值误差的估计问题,但是同时也使得插值函数值的计算变得复杂。
依照线性插值和二次插值的思路,可以增加基函数分子和分母的阶数,构造拉格朗日插值多项式:
一个n次的拉格朗日插值函数可以绘制经过(n+1)个节点的曲线,但运算量非常大。而且在次数比较高时,容易产生剧烈的震荡(龙格现象)。所以要选择位置特殊的节点(比如切比雪夫多项式的零点)进行插值,或使用多个次数较低的拉格朗日函数分段插值。(关于拉格朗日多项式和龙格现象,详见维基百科链接)
分段插值实现代码如下:
- //n为次数,nmax为节点的总数。n不大于nmax
- void lagrange(float p[][2],int n,int nmax)
- {
- float x,y;
- int i,j,t;
- float temp;
- glColor3f(0.0,0.0,1.0);
- for(i=0;i<=(nmax-1);i+=(n-1))
- {
- glBegin(GL_LINE_STRIP);
- for(x=p[i][0];x<=p[i+n-1][0];x+=1.0)
- {
- y=0.0;
- for(j=0;j
- {
- temp=1.0;
- for(t=0;t
- {
- if(t==j)
- continue;
- temp*=(x-p[i+t][0])/(p[i+j][0]-p[i+t][0]);
- }
- y+=temp*p[i+j][1];
- }
- glVertex2f(x,y);
- }
- glEnd();
- }
-
}
使用4次拉格朗日多项式分段插值:
转化为灰度:
拉格朗日多项式插值也存在连接处不光滑的问题。
如果直接使用20次的拉格朗日插值,得到的图像如下:
这样的插值曲线显然是不能容忍的~
牛顿插值
从算法角度考虑,提出便于计算的插值方法,也就是牛顿插值公式。 拉格朗日插值每增加一个节点,整个函数要重新计算,计算量巨大。而牛顿插值每增加一个点只需要在多项式的最后增加一项,而且各基函数的系数可以递归计算,减少了很多计算量。
均差(Divided differences)
是递归除法过程。在数值分析中,也称差商(Difference quotient),可用于计算牛顿多项式形式的多项式插值的系数。
定义
[数值分析 钟尔杰 电子科大]
|
阶差商 |
阶差商 |
阶差商 |
阶差商 |
|
阶差商 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
差商表(高阶差商是两个低一阶差商的差商)
由函数表出发,从上往下从左往右依次计算出一阶,二阶, 。。。,各阶均差。
[wikipedia均差]
牛顿多项式
将n次插值多项式写作如下形式:
也就是牛顿插值公式中的各项系数就是均差表中计算出的各阶均差的第一个数据!
即牛顿插值公式为:
[wikipedia牛顿多项式]
[wikipedia均差小节:牛顿插值法]
实现代码如下:
- void newton(float p[][2],int n,int nmax)
- {
- float x,y;
- int i,j,t;
- float temp;
- float f[20][20];
- glColor3f(0.0,0.0,1.0);
- for(i=0;i<=(nmax-1);i+=(n-1))
- {
- for(t=0;t
- {
- f[t][0]=(p[i+t][1]-p[i+t+1][1])/(p[i+t][0]-p[i+t+1][0]);
- for(j=1;j<=t;j++)
- f[t][j]=(f[t-1][j-1]-f[t][j-1])/(p[i+t-j][0]-p[i+t+1][0]);
- }
- glBegin(GL_LINE_STRIP);
- for(x=p[i][0];x<=p[i+n-1][0];x+=1.0)
- {
- y=p[i][1];
- temp=1.0;
- for(j=0;j
- {
- temp*=x-p[i+j][0];
- y+=temp*f[j][j];
- }
- glVertex2f(x,y);
- }
- glEnd();
- }
-
}
可能由于计算精度的原因,牛顿插值绘制的曲线与拉格朗日插值的曲线略有不同。但次数较高时,牛顿插值也会产生剧烈的震荡。分段4次牛顿插值图像如下:
转化成灰度如下:
牛顿插值也存在连接处不光滑的缺陷。
埃尔米特插值
以上各多项式插值方法的插值条件都是各节点的坐标,在以低阶函数分段插值时虽然可以保持曲线的稳定(比较平缓),但在各分段曲线的连接处无法保持光滑(一阶导数相等)。埃尔米特插值方法不但规定了各节点的坐标值,还规定了曲线在每个节点的各阶导数,这样就可以既保持曲线的稳定,又保证在连接处足够光滑。
以3次二重("m重"就是规定坐标和曲线在所有节点处1到m-1阶导数的值)埃尔米特插值为例:
4个基函数满足分别只在y0,y1,y0的导数,y1的导数处等于1,而在其他3个条件下等于0。可以把埃尔米特插值看作对坐标和导数的插值的组合。
曲线在每个节点的导数可以根据相邻节点和它的相对位置确定,也可以完全随机生成。只要位置比较高和比较低的节点的导数绝对值不是很大,就可以使整条曲线落在最高与最低节点定义的带状区域内,这样就可以避免对插值的截取。
对于本节的示例节点,一种可能的导数值如下:grad[20]={-4.0,4.0,0.5,-2.0,1.0,-2.0,-2.0,2.0,1.0,1.0,0.0,-1.0,-4.0,3.0,0.0,-3.0,3.0,0.0,-4.0,-4.0};
实现代码如下:
- //p[i][0],p[i][1]为点i的坐标,p[i][2]为曲线在点i的导数
- //nmax为节点的总数
- void hermite(float p[][3],int nmax)
- {
- float x,y;
- float a1,a0,b1,b0;
- float x00,x11;
- int i;
- float temp;
- glColor3f(0.0,0.0,1.0);
- for(i=0;i
- {
- glBegin(GL_LINE_STRIP);
- x00=p[i][0];
- x11=p[i+1][0];
- for(x=p[i][0];x<=p[i+1][0];x+=1.0)
- {
- temp=(x11-x00)*(x11-x00);
- a0=(x11-3*x00+2*x)*(x11-x)*(x11-x)/temp/(x11-x00);
- a1=(-x00+3*x11-2*x)*(x-x00)*(x-x00)/temp/(x11-x00);
- b0=(x-x00)*(x-x11)*(x-x11)/temp;
- b1=(x-x00)*(x-x00)*(x-x11)/temp;
- y=a0*p[i][1]+a1*p[i+1][1]+b0*p[i][2]+b1*p[i+1][2];
- glVertex2f(x,y);
- }
- glEnd();
- }
-
}
分段3次埃尔米特插值图像如下:
转化为灰度如下:
可见虽然n节点的埃尔米特插值是由(n-1)段曲线构成,但在每一个连接处都是光滑的。
样条插值
B-样条
B-样条是Bezier样条的一般化,也可推广为NURBS样条。先来介绍一下B-样条:
该式定义了一个n次的B-样条,它有(m+1)个控制点(样条曲线的"节点"称作控制点,因为这些点控制曲线的弯曲方向和程度,但曲线不一定经过这些点),也就有(m+1)个基函数。一般绘制的是完整的曲线,u(min)取0,u(max)取1。当u取值均匀时,该样条称作均匀B-样条。当m=n时,B-样条退化为Bezier样条。
函数绘制的曲线始终落在其控制点的凸包(包含一个点集所有点的凸多边形,而且该凸多边形所有顶点都来自这个点集)中。对于一个n次的B-样条,改变一个控制点的位置,只改变它所在的n段曲线(由n+1个控制点定义,且以该点起始)的形状,而不对其余的(m-n)段曲线产生影响。
Bezier样条
Bezier(贝塞尔)样条是法国工程师皮埃尔·贝塞尔(Pierre Bézier)在1962年为了设计汽车主体外形曲线而提出的。其一般式表达式为:
其中,u取值为[0,1],pk(k=0,...,n)为(n+1)个节点,n称为阶数。
Bezier样条还可以递归定义为:
含义是n阶Bezier样条是两条(n-1)阶Bezier样条的插值。
当阶数降为1时,Bezier插值退化成线性插值。改变任意一个控制点的位置,整条曲线的形状都会发生变化。
比较常用的Bezier样条是3次Bezier:
Beizer样条在首尾端的切线是前两个点和最后两个点的连线。除了第一个点和最后一个点,其他控制点一般都不在曲线上。
3阶(4控制点)的Bezier函数图像如下:(黑色曲线为Bezier曲线,蓝色折线为控制点的连线)
Bezier样条可以实现非常快速的运算。为了方便说明,将3次Bezier样条表示成如下形式:
对于任意给定的u,可以通过合并的方式将原来的7次乘法、4次加法减少为3次乘法、3次加法:
一般情况下,应用Bezier样条绘制曲线时,都是先给定一个很小的步长t(步长足够小才能保证Bezier曲线的精确),让t从0取到1,从头到尾绘制整条曲线。在t不变的条件下,可以使用更快速的差分方法,利用前一个点计算出下一个点的值,将每步的计算量减小到只有3次加法:
只需要在绘制曲线之前计算4个常数,就可以很快地计算出曲线上的所有点:
采用这种方式,Bezier样条的运算量只随阶数线性增长。
实现代码如下:
- void bezier3(float xx0,float yy0,float xx1,float yy1,float xx2,float yy2,float xx3,float yy3)
- {
- GLint i;
- GLfloat x,y;
- GLdouble ax,bx,cx,ay,by,cy;
- GLdouble t;
- GLdouble dx,d2x,dy,d2y,delta;
- GLdouble d3x,d3y;
- ax=-xx0+3.0*xx1-3.0*xx2+xx3;
- bx=3.0*xx0-6.0*xx1+3.0*xx2;
- cx=-3.0*xx0+3.0*xx1;
- ay=-yy0+3.0*yy1-3.0*yy2+yy3;
- by=3.0*yy0-6.0*yy1+3.0*yy2;
- cy=-3.0*yy0+3.0*yy1;
- delta=0.0005;
- d3x=6.0*ax*delta*delta*delta;
- d3y=6.0*ay*delta*delta*delta;
- x=xx0;
- y=yy0;
- glBegin(GL_LINE_STRIP);
- glVertex2f(x,y+200);
- d2x=6.0*ax*delta*delta*delta+2.0*bx*delta*delta;
- dx=ax*delta*delta*delta+bx*delta*delta+cx*delta;
- d2y=6.0*ay*delta*delta*delta+2.0*by*delta*delta;
- dy=ay*delta*delta*delta+by*delta*delta+cy*delta;
- for(t=0.0;t<=1.0;t+=delta)
- {
- d2x+=d3x;
- dx+=d2x;
- x+=(float)dx;
- d2y+=d3y;
- dy+=d2y;
- y+=(float)dy;
- glVertex2f(x,y);
- }
- glEnd();
-
}
NURBS样条
NURBS(Non-Uniform Rational B-Splines 非均匀有理B-样条),是贝塞尔样条的推广。"非均匀"的意思是控制点的间隔可以是不均匀的,"有理"的意思是各控制点带有不同的权值。和Bezier样条相比,它对曲线形状的控制更自由:
其基函数B(k,d)与B-样条的基函数相同,w(k)为各点的权因子。和B-样条一样,改变一个控制点的位置,只改变它所在的n段曲线的形状,而不对其余的(m-n)段曲线产生影响。
插值的一些应用
噪声
噪声图像一般需要二维或三维插值函数,不过了解了各一维插值函数,就很容易扩展到二维和三维了。关于二维噪声图像的产生,请参见《二维噪声图像》。
水波
下面这个图像就是用插值函数绘制的模拟水波的三维网格(静态图):
虽然这张网格看起来似乎需要二维插值,但这张网格是由6个不同波长和频率的Gestner合成的,每个独立的波形只需要一维插值生成。
[常用的插值函数 ]
from: http://blog.csdn.net/pipisorry/article/details/62227459
转:http://blog.csdn.net/pipisorry/article/details/62227459
来自