Knight Moves (骑士跳跃)

Description

 

A friend of you is doing research on the Traveling Knight Problem (TKP) where you are to find the shortest closed tour of knight moves that visits each square of a given set of n squares on a chessboard exactly once. He thinks that the most difficult part of the problem is determining the smallest number of knight moves between two given squares and that, once you have accomplished this, finding the tour would be easy.

Of course you know that it is vice versa. So you offer him to write a program that solves the "difficult" part.

Your job is to write a program that takes two squares a and b as input and then determines the number of knight moves on a shortest route from a to b.

Input Specification

The input file will contain one or more test cases. Each test case consists of one line containing two squares separated by one space. A square is a string consisting of a letter (a-h) representing the column and a digit (1-8) representing the row on the chessboard.

Output Specification

For each test case, print one line saying "To get from xx to yy takes n knight moves.".

Sample Input

e2 e4

a1 b2

b2 c3

a1 h8

a1 h7

h8 a1

b1 c3

f6 f6

Sample Output

To get from e2 to e4 takes 2 knight moves.

To get from a1 to b2 takes 4 knight moves.

To get from b2 to c3 takes 2 knight moves.

To get from a1 to h8 takes 6 knight moves.

To get from a1 to h7 takes 5 knight moves.

To get from h8 to a1 takes 6 knight moves.

To get from b1 to c3 takes 1 knight moves.

To get from f6 to f6 takes 0 knight moves.



解题思路：

1．由原始问题引出的3个问题

（1）求任意两点间的最短步数

该问题不需要求出该两点间的路径上的点，也不需要求出拥有该最短步数的路径个数，只需将其间的最短步数求出即可；

（2）求任意两点间的所有最短路径及其全部信息

路径信息：路径上的每一点

该问题不仅需要求出两点间的最短路径，且要求出这样的最短路径有多少条和每一条路径上的每一点

（3）骑士周游世界问题

在一个8×8的方格棋盘中，按照国际象棋中马的行走规则从棋盘上的某一方格出发，开始在棋盘上周游，如果能不重复地走遍棋盘上的每一个方格，这样的一条周游路线在数学上被称为国际象棋盘上汉密尔顿链，求从任意一点出发，所有这样的汉密尔顿链及其全部信息；

 

 

2．问题分析

（1）棋盘的表示方法

可以用一个9×9的二维数组chess[9][9]来表示国际象棋的棋盘，在马还没有开始行走时，棋盘上所有的格都置为零，以后，马跳到哪个格，就将马跳跃的步数加1后的值记录在相应的空格里；开始点在行走前设为1；

注：为表示方便，取9×9，数组均下标从1开始；

 

（2）马的跳跃方向

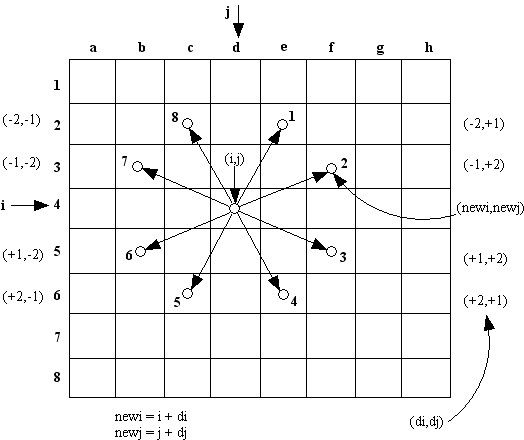
在国际象棋的棋盘上，一匹马共有8个可能的跳跃方向，如图1所示，按顺时针分别记为1~8，设置一组坐标增量来描述这8个方向；

 

 

（3）马的跳跃方向的表示

设i表示行，j表示列，行增量为di，列增量为dj，设马向某个方向试探性地跳跃一步之后的新坐标为(newi,newj)，则有：

newi = i + di

newj = j + dj

其每个方向的增量如图所示，表示为(di,dj)

 

（4）基本过程

设当前点(i,j)，方向k，沿方向k跳一步后的新点(newi,newj)；每走一步，都要判断新点(newi,newj)是否还在棋盘上：

若1£newi£8且1£newj£8，则新点仍在棋盘上，则还需判断该点是否已经走过，即

若chess[newi][newj]=0，表示该步可走；

若chess[newi][newj]=1，表示该点已经走过，不能再走，放弃当前方向，并转向下一个方向试探；

否则，直接放弃当前方向，并转向下一个方向试探；

 

（5）有关两点间最短路径的定义

最短路径步数minstep：马跳的次数

拥有该步数的路径个数minstepcount：这样的路径有minstepcount条

最短路径上的点：每一条拥有该步数的路径上的点

knight 在点(i,j) 沿着 k 方向走一步,到达新点 (newi,newj)

i    : 走一步前的行下标 (i>=1 and i<=8)

j    : 走一步前的列下标 (j>=1 and j<=8)

k    : 方向 (k>=1 and k<=8)

newi : 走一步后的行下标 (newi>=1 and newi<=8)

newj : 走一步后的列下标 (newj>=1 and newj<=8)

 

3．求解算法

算法1：找出从S出发到达D的所有路径长度小于6的路径，然后再从这些路径中寻找最短路径

算法2：基于1的思想，但在搜索的过程中就开始求最短路径的长度，用变量代替回溯的值，若当前搜索的点已经超过当前最短路径长度，则从这个点回溯，从点出发的8个方向均不需要搜索，即在搜索树中，该点的儿子节点直接跳过；

注意：采用的算法不同，其数据结构就不同。

【借鉴了路人的，感觉还不错，分享给朋友们】

 

程序代码：

 

#include <stdio.h>

    #include <string.h>

    #include <queue>

    using namespace std;



    int step;

    int to[8][2] = {-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2,-2,-1};//骑士移动的8个方位

    int map[10][10],ex,ey;

    char s1[5],s2[5];



    struct node

    {

        int x,y,step;

    };



    int check(int x,int y)

    {

        if(x<0 || y<0 || x>=8 || y>=8 || map[x][y])

        return 1;

        return 0;

    }



    int bfs()

    {

        int i;

        queue<node> Q;

        node p,next,q;

        p.x = s1[0]-'a';

        p.y = s1[1]-'1';

        p.step = 0;

        ex = s2[0]-'a';

        ey = s2[1]-'1';

        memset(map,0,sizeof(map));

        map[p.x][p.y] = 1;

        Q.push(p);

        while(!Q.empty())

        {

            q = Q.front();

            Q.pop();

            if(q.x == ex && q.y == ey)

            return q.step;

            for(i = 0;i<8;i++)

            {

                next.x = q.x+to[i][0];

                next.y = q.y+to[i][1];

                if(next.x == ex && next.y == ey)

                return q.step+1;

                if(check(next.x,next.y))

                continue;

                next.step = q.step+1;

                map[next.x][next.y] = 1;

                Q.push(next);

            }

        }

        return 0;

    }



    int main()

    {

        while(~scanf("%s%s",s1,s2))

        {

            printf("To get from %s to %s takes %d knight moves.\n",s1,s2,bfs());

        }

        return 0;

    }