小米语音首席科学家Daniel Povey:下一代Kaldi将走向何方?
如果你曾为《十面埋伏》中章子怡“听音辨鼓”的神技所惊艳,那么你也许就会被语音识别工具Kaldi的神通广大所倾倒。作为当前最流行的开源语音识别开发框架,Kaldi集成了多种语言识别模型,并被工业界、学术界几乎所有语音团队所采用。Daniel Povey博士,作为誉满业界的Kaldi之父,他对下一代Kaldi以及其中所包含技术的发展又有何新的思考呢?在2020北京智源大会的主题报告《可微分的加权有限状态机及其机器学习应用》中,Daniel Povey为我们揭晓了答案。
Daniel Povey,开源语音识别工具Kaldi之父,前约翰霍普金斯大学语言与语音处理中心研究型副教授,现任小米集团语音首席科学家。
在演讲中,Daniel Povey首先指出了当前版本Kaldi的一些缺陷,并提出了一些下一代Kaldi发展方向的战略构想;其次,就“加权有限状态机”这一关键技术以及其在下一代Kaldi中如何应用进行了阐述;在报告的尾声,Daniel历数传统确定化算法的优缺点并阐述了其算法的主要思想。
整理:智源社区 李维
一、Kaldi及其下一代
Kaldi,得名于传说中发现了咖啡树的埃塞俄比亚牧羊人,其诞生于2009年约翰霍普金斯大学(Johns Hopkins University)的一个名为“新语言和新领域的低开发成本和高质量语音识别”的研讨会。作为语音识别领域的后起之秀,Kaldi已被工业界和学术界的从业者所广泛接受,俨然成为当前最流行的开源语音识别工具。Kaldi主要使用C及C++进行开发编写,在此之上使用Bash和Perl以及Python脚本调用C++代码进行工具开发。
Kaldi有着与HTK相仿的目标和受众,拥有很多处理实际任务的实例以及大量可以复用的脚本是其广受欢迎的众多原因之一,其鲜明特色主要包括:
1)与有限状态传感器(FSTs)的代码级集成;
2)广泛的线性代数支持,包括一个封装了标准的BLAS和LAPACK例程的矩阵库;
3)可扩展设计;
4)开放式许可。
Kaldi的优点不可否认,但其十分复杂以及没有专长技能作为前提则不易学会的缺点也饱受诟病。此外,因为Kaldi本身不支持整数化,故很难在手机上实现产品化。虽说Kaldi使用的是自己的深度学习框架,但这个框架并不容易使用。Daniel Povey也在本次报告中直言不讳地指出“尽管Kaldi拥有自己的神经网络框架,但其通用程度却不及PyTorch和TensorFlow”,故他便有了将PyTorch应用到下一代Kaldi深度神经网络中且允许在PyTorch和TensorFlow之间实现灵活切换的想法。如若这个想法在下一代Kaldi中得以实现,那将使得Kaldi与标准框架PyTorch和TensorFlow实现更好的结合。
图1:下一代Kaldi框架图
Daniel Povey表示,下一代Kaldi将非常不同,几乎没有与现有Kaldi通用的代码,他希望下一代Kaldi能实现以下目标:
1)用少量代码就实现像联结主义时间分类算法(CTC)这样的功能;
2)轻松有效地整合“离散”信息源,如词汇及电话序列信息等;
3)将“传统”自动语音识别(ASR)解码与PyTorch模型以简单的方式集成;
4)有效地操作序列和序列集合;
5)使用通用而不是过于具体的工具来执行操作。
尽管下一代Kaldi注定会有所变革,但Daniel表示在创造一系列工具用以实现这一目标之前,有限状态机是一个不得不解释的概念。
二、有限状态机
2.1 何为有限状态机
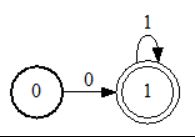
有限状态机,也被简称为FSA(Finite State Acceptors),其主要被用以研究具有有限内存的计算过程,并根据一定的规则响应外界输入值,对研究对象的状态变化进行枚举,得出状态变化序列。作为一种依据对象行为建模的工具,其被广泛应用于电路设计、软件工程、网络协议和语言研究等计算机科学中的众多领域。如图2所示即为一个极为简单的有限状态机,图中两个圆圈称为节点,用以表示两种状态,并分别用0和1记之。在任意时刻有限状态机均处于有限状态集合的某一状态,其中有限状态集合可被一般地表示为{状态1,状态2,…,状态m},m需为一有限数,这是其之所以被称之为有限状态机的原因和要求。
图2:一个简单的有限状态机
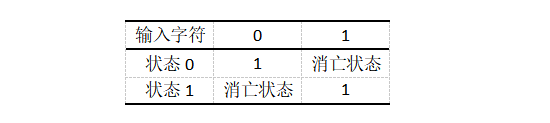
从图中不难看出,从每个节点或是状态出发都有一条边,复杂的有限状态机则有多条边并通向多种状态。处于某一状态的有限状态机在获得输入字符时会引起状态转换,将从当前状态转换到下一状态或是仍然保持当前状态不变化,其依据就是输入字符是否跟该节点出发的某条边的内容一致。例如,若有限状态机目前正处于状态0且输入字符也为0,那么该有限状态机则会从状态0进入状态1。对于状态1而言,若输入的字符为1,则其会保持当前状态不变。倘若当前状态不存在与输入字符对应的输出边,那么该有限状态机就会进入消亡状态(Doom state)。例如,当有限状态机处于状态0时输入字符1或是在状态1时输入字符0。此外,对图示有限状态机而言,输入任何非0和1的字符均会导致该状态机进入消亡状态。为方便和直观,一般绘制如表1所示状态转换表。
表1:有限状态机转换表
Daniel Povey指出,有限状态机中有两个特殊的状态,被称为起始状态和结束状态。当有限状态机开始工作,输入字符会导致状态机的状态不断变化,但只要最后输入的那个字符使得状态机能转化到结束状态,那么该状态机就会结束工作,识别出所输入的所有字符序列。例如,在图1中假定状态0和状态1分别为起始和结束状态,那么该有限状态机就会接收“0”,“0 1”,“0 1 1”,“0 1 1 1”等字符串。由于该状态机设置得较为简单,故其在该种情况下只能接受类似的有限字符串。倘若输入的字符串为“0 1 0”,那么由于字符0导致状态机会进入消亡状态,故该字符串将被状态机所拒绝。
除了有限状态机之外,加权有限状态机作为有限状态机的一种特殊形式亦是构建快速语音识别系统的主流技术。
2.2 加权有限状态机
在语音识别领域有着广泛应用的加权有限状态机(Weighted Finite State Acceptors,WFSA)事实上是以有限状态机为蓝本,顾名思义,在其输出边或弧上拥有权值信息。
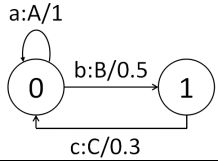
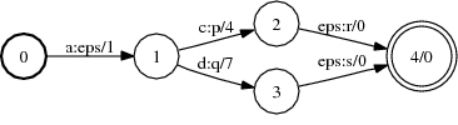
图3:一个简单的加权有限状态机
如图3所示即为一个简单的加权有限状态机,不难发现其是一个有向图。连接各状态之间的状态转移弧上分别标示着输入符号、输出符号以及相应的权值信息。图中所示的输入和输出符号有所不同,但在现实情况中允许一个加权有限状态机具有相同的输入和输出符号。图中的状态机会在输入小写英文字母之后输出相应的大写字母,而在实际的语音识别应用中,可能是以发声的声韵母作为输入符号,并以汉字或是词语作为输出。
一般而言,加权有限状态机除了以状态转移弧和结束状态赋有权值为显著特点之外,还需要半环代数理论作为支撑。一个简单的半环代数结构通常由元素集合、两个二元运算和两个基本单元构成,可被形式化表示为。应当特别指出,这里的0和1并不是真正的实数0和1,而是代指零元和幺元。半环代数需满足的公理和条件有加法的结合律和交换律、乘法的结合律、分配律等。具体如表2所示:
表2:半环代数所满足的公理
表3则显示了一些常用的半环。在语音识别领域使用频率较高的半环有Log半环(Log semiring)和热带半环(Tropical semiring)。在Log半环中,权值被当作负对数概率来处理,概率在并行路径上求和。在热带半环中,权重值被视为类似于成本之类东西(例如,距离),并以使成本最小化作为合并并行路径时的语义。
表3:一些常用的半环
在谈及加权有限状态机在下一代Kaldi中的应用时,Daniel Povey表达了以下想法:
1)在下一代中,会将权重与有限状态机的结构分开,并尽可能忽略权重;
2)用相反的符号存储权重,比如负定的Cost或Logprob之类的,并称之为“分数”;
3)获取权重信息的操作支持两种类型:一个相当于“热带半环”(取最大值),另一个相当于“Log半环”(取Log Sum Exp或Soft Max);
4)或许将采用更一般的权重类型,但其或只能通过标量与核心算法交互,例如Pruning算法。
三、有限状态机确定化
有限状态机确定化(FSA determination)是对有限状态机的基本操作之一,其他基本操作还有合并操作、组合操作以及权重推移操作等等。对一个有限状态机进行确定化操作的目的是为去除原始有限状态机的冗余,得到一个等效的确定的有限状态机,使得该状态机能接收与原始状态机一样的路径集。
3.1 确定化操作的意义
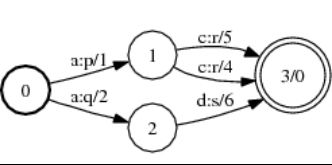
对于确定化有限状态机的每一个状态来说,同一个输入符号有且只有一个转移弧。例如,在图4的原始加权有限状态机中,对于状态3来说有两条具有同样输入和输出字符但不同权重的状态转移弧与之对应,而被确定化之后得到的图5所示的加权有限状态机则不会出现类似情况。那么由此可见,进行确定化操作之后的加权有限状态机相较原始状态机而言就具有了非冗余性。当给一个确定化的有限状态机输入符号序列时,该状态机最多只有一条路径与输入字符序列相对应,如此以来搜索算法的时间和空间复杂度就会被降低,这也是确定化操作的作用之所在。
图4:原始加权有限状态机
(http://www.openfst.org/twiki/bin/view/FST/DeterminizeDoc)
图5:进行确定化操作之后的加权有限状态机
(http://www.openfst.org/twiki/bin/view/FST/DeterminizeDoc)
Daniel Povey在谈及有限状态机确定化时指出其是一个非平凡的且具有不规则结构的算法,并希望就该算法而言能做到以下几点:
1)期望能够在GPU上将其实现;
2)可阐述计划在下一代Kaldi中使用的一些数据类型和抽象概念;
3)期望下一代Kaldi比有限状态机更加通用;
4)试图扩展能在GPU上实现轻松编码的范围。
3.2 确定化算法间的比较
Daniel Povey在介绍他的基于热带半环的确定化算法前列举了一些传统算法的特点和不足,其中包括传统的不加权算法以及加权算法。关于传统的不加权算法,Daniel Povey认为它有如下特点:
1)输出中的每个状态对应于输入中的一个状态子集;
2)输出中的初始状态对应于{0},即输入中的起始状态;
3)需维护要处理的输出状态队列;
4)需维护从输入状态ID到输出状态ID的映射。
关于传统的加权算法,Daniel Povey指出:
1)加权后映射是从输入状态ID的加权集合到输出状态ID;
2)权重需要以某种方式标准化,例如,在传统的热带半环中,权重要使最小成本为0;
3)标准化删除的额外权重(Extra weight)将成为输出弧上的权重;
4)会破坏并行性并具有糟糕的浮点数舍入属性。
这里所谓的并行化包含(1)批量确定状态;(2)首批仅有一个元素;(3)批量处理的规模取决于有限状态机拓扑结构;(4)可在实际中的某个小批量中并行处理多个有限状态机等特性。
关于Daniel Povey所提出的确定化算法,他总结到:
1)将状态子集表示为(起始状态,符号序列)这种形式是映射的关键;
2)子集是从起始状态通过符号序列可到达的状态的集合;
3)标准化过程包括删除符号序列前缀和推进初始状态;
4)输出弧上的“分数”将是标准化中删除的输入弧的“分数”之和;
5)需要进行确定化操作的有限状态机将更少。
3.3 数据结构:列表套列表
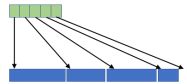
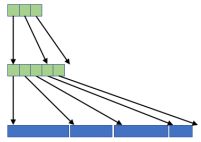
在报告中Daniel Povey还提及一种名为列表套列表(ListOfList)的数据结构,其在存储一组固定类型的(大小可变)列表时,采用类似图6(a)所示将其连接在一起的形式,并按图6(b)的形式存储与每个子数组开头相对应的索引,再加上一个子数组结束后的索引。此外,利用此思想还可以处理三维及多维不规则数组,只需额外增加索引数量即可,图6(c)所示。通常来讲,列表套列表型结构有两种检索方式:其一为分层索引(Hierarchical indexing),比如list[i][j],就像通常索引向量
(a)
(b)
(c)
图6:列表套列表
四、总结
在报告的尾声,Daniel表示其已经以有限状态机确定化操作为例,设计用于处理不规则结构的并行计算框架,愿景是使其能够拓展PyTorch乃至TensorFlow等框架平台。此外,他还提到已经开始了关于非GPU实现的工作,并希冀该工作不仅局限于设计一个自动语音识别(ASR)工具包。
从有限状态机到加权有限状态机,从Kaldi到其下一代,技术的不断发展进步促使着工具的不断更新演变,而工具使用中所暴露出的问题又是下一次技术进步的动力和源头。正是在这样的互相促进中,Daniel Povey博士及其团队酝酿着Kaldi这一语音识别工具持续向更好、更优、更加完美的方向发展。但“金无足赤,人无完人”,正如Kaldi作为“后浪”曾席卷了它的前任们一样,未来会不会有另一工具成为Kaldi的下一个继任者呢?会不会有另一巨匠能够站在Daniel Povey的肩膀之上呢?让我们拭目以待!
将我们设为星标⭐
就能及时收到推送啦
![]()
关于我们
北京智源人工智能研究院(Beijing Academy of Artificial Intelligence,简称BAAI)成立于2018年11月,是在科技部和北京市委市政府的指导和支持下,由北京市科委和海淀区政府推动成立的新型研发机构。
//智源研究院简介
///
学术思想 | 基础理论 | 顶尖人才 | 企业创新 | 发展政策
![]()