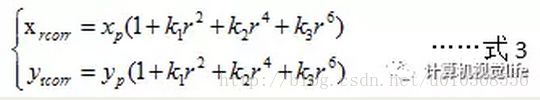单目相机标定
一.概述
1.作用:相机标定的目的就是要获得相机的内参数,得到二维平面像素坐标和三维世界坐标的关系,从而进行三维重建。
2.基本概念:
- 图像坐标系(以像素为单位和以毫米为单位)
- 相机坐标系
- 世界坐标系
图像坐标系
是一个以像素为单位的坐标系,它的原点在左上方,每个像素点的位置是以像素为单位来表示的,所以这样的坐标系叫图像像素坐标系(u,v),u和v分别表示像素在数字图像中的列数和行数,但是并没有用物理单位表示像素的位置,因此还需建立以物理单位表示的图像坐标系,叫图像物理坐标系(x,y),该坐标系是以光轴与图像平面的交点为原点,该点一般位于图像中心,但是由于制造原因,很多情况下会偏移。以毫米为单位。两个坐标轴分别与图像像素坐标系平行。
即:像素坐标(u,v) 物理坐标(x,y)
![]()
若图像物理坐标系的原点在图像像素坐标系中的坐标为(u0,v0),每个像素在图像物理坐标系中的尺寸为dx,dy,则两个坐标系的关系为:
![]()
化为齐次坐标和矩阵形式:
![]()
相机坐标系
是以相机的光心为原点Oc,Zc轴与光轴重合,与成像平面垂直,Xc和Yc轴与图像坐标系的两个坐标轴平行。OOc为摄像机的焦距,即相机坐标系的原点与图像物理坐标系原点之间的距离。
世界坐标系
是由用户定义的三维坐标系,用于描述三维空间中的物体和相机的位置。表示为XwYwZw。
三者可用如下图表示:
![]()
二.变换关系
1.世界坐标系![]() 相机坐标系:
相机坐标系:
![]()
由一个旋转矩阵R和一个平移向量t来描述
化为齐次坐标:
![]()
2. 相机坐标系![]() 图像物理坐标系:
图像物理坐标系:
![]()
化为齐次坐标:
![]()
3.世界坐标系![]() 图像坐标系:
图像坐标系:
![]()
其中是相机的M1内参数,M2是外参数。
三.透镜畸变
透镜的畸变主要分为径向畸变和切向畸变,还有薄透镜畸变等等,但都没有径向和切向畸变影响显著,所以我们在这里只考虑径向和切向畸变。
1.径向畸变
径向畸变是由于透镜形状的制造工艺导致。且越向透镜边缘移动径向畸变越严重。下图所示是径向畸变的两种类型:桶形畸变和枕形畸变。
实际情况中我们常用r=0处的泰勒级数展开的前几项来近似描述径向畸变。矫正径向畸变前后的坐标关系为:
由此可知对于径向畸变,我们有3个畸变参数需要求解。
2. 切向畸变
切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致。因此,如果存在切向畸变,一个矩形被投影到成像平面上时,很可能会变成一个梯形。切向畸变需要两个额外的畸变参数来描述,矫正前后的坐标关系为:
由此可知对于切向畸变,我们有2个畸变参数需要求解。
综上,我们一共需要5个畸变参数(k1、k2、k3、p1和p2 )来描述透镜畸变。
注:
opencv畸变模型
径向畸变模型:
xc= xd (1+k1r^2 +k2r^4 +k3r^6+⋯)
yc= yd (1+k1r^2 +k2r^4 +k3r^6+⋯)
切向畸变模型:
xc= 2p1xdyd+p2 (r^2 +2xd^2 )
yc= 2p2xdyd+p1 (r^2 +2yd^2 )
可得:
xc= xd (1+k1r^2 +k2r^4 )+2p1xdyd+p2 (r^2 +2xd^2 )
yc= yd (1+k1r^2 +k2r^4 )+2p2xdyd+p1 (r^2 +2yd^2 )
xd,yd为图像中的点(存在畸变),xc,yc是畸变校正后的点。
由公式可得畸变有k1,k2,k3,p1,p2五个参数,对于质量比较好的相机来说,切向畸变很小,可忽略,径向畸变系数k3也可忽略,只计算k1,k2两个参数。张正友标定中就默认为p1,p2为0。(即不考虑切向畸变)