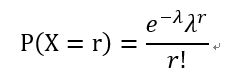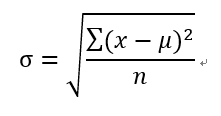用Excel做直方图（1）：随机数发生器

在介绍用Excel做直方图前，先来介绍用Excel生成随机数的功能，在我看来，这两个功能还是很息息相关的，放在一起学习可以更深入的理解统计学里各种分布的概念。

 

本节知识点：

• 数据分析工具库：随机数发生器

• 离散变量和连续变量

• 均匀分布、二项分布、伯努利分布、泊松分布、正态分布、离散概率分布

 

Excel 2016 有个数据分析的功能，可以满足数据分析小白们用Excel做数据分析的绝大多数需求。

 

具体位置在数据——数据分析

 

上一节已经介绍过其中的一个功能了——相关系数，这个小节再来介绍另一个功能——随机数发生器。

 

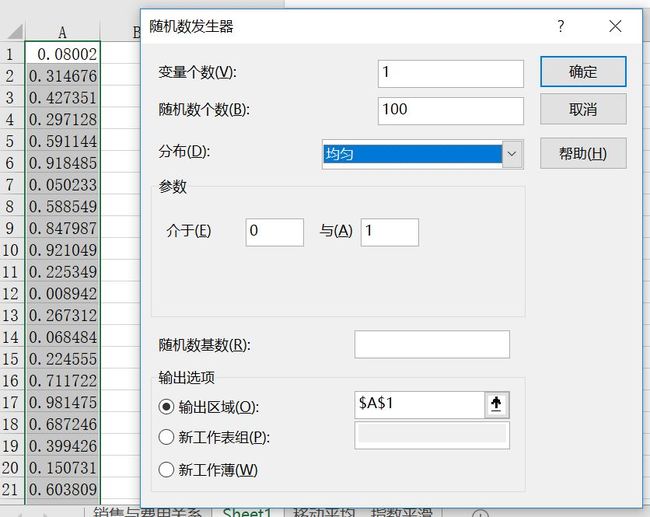
随机数发生器，顾名思义，用来生成随机数。发生器中的几个参数含义如下：

• 变量个数：输出数据中想要的列数

• 随机数个数：输出数据中想要的随机数的个数

• 分布：随机数分布的方法。有均匀、正态、伯努利、二项式、泊松、模式、离散分布

• 参数：选择不同的分布会出现不同的参数，稍后一一讲解。

• 随机数基数：在此输入用来产生随机数的可选数值。可在以后重新使用该数值来生成相同的随机数。

• 输出选项：输出可以是该工作表的某一个区域，也可以是新工作表或新工作簿。

 

一、均匀

均匀的随机数的参数是介于XX与XX，一个表示下限，另一个表示上限，用于生成上下限之间的均匀的连续性随机数，相当于函数RAND（），这个函数默认是生成0到1之间的连续随机数，可以自己再构造上下限。如下图所示，这里用随机数发生器均匀分布产生了1列100个介于0到1之间的随机数。

 

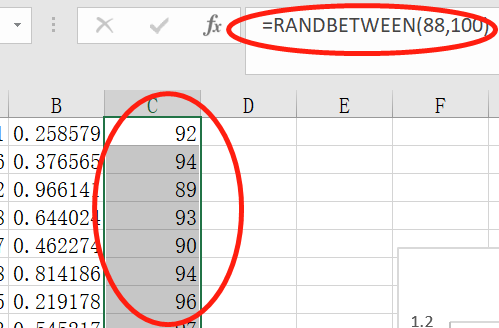
在统计学里变量按变量值是否连续可以分为连续型变量和离散型变量，连续型变量就是在一定区间内可以任意取值，相邻的两个数值可以无限分割，其取值范围为实数，而离散型变量通常以整数取值，数据由一个一个单独的数值组成，公式里除了RAND生成随机数外，还有一个RANDBETWEEN（下限，上限），产生的是离散型的随机数。

 

对比一下就能明白连续和离散的区别了，上图，B列是RAND函数产生的0~1之间的随机数，也就是随机数发生器——均匀产生的随机数，C列是RANDBETWEEN函数产生的离散型随机数，可以看出，离散型随机数是一个个单独的数值，连续型随机数是实数随机均匀的。

 

二、二项式

二项分布条件：

• 进行一系列独立试验

• 每一次试验都存在成功和失败的可能，且成功的概率相同

• 试验次数有限

   

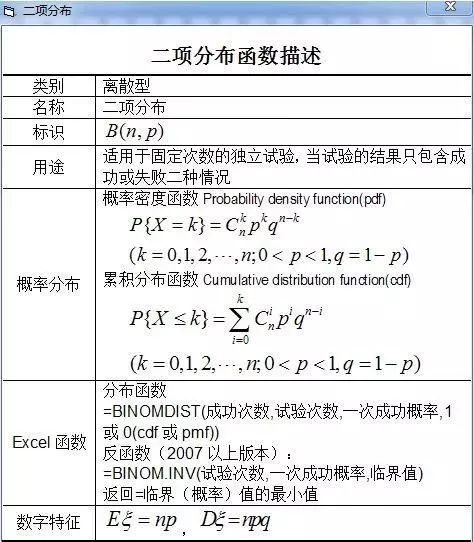
    二项分布记做：X~B(n,p)，X表示n次试验中的成功次数,我们要求的是成功的次数，其概率为：

p是每次试验成功的概率，q=1-p是每次试验失败的概率，其中，

 

二项分布的期望E(X)=np，方差Var(X)=npq，二项分布是离散型概率分布。

 

具体到随机数发生器中，我们生成1列10个随机数，参数P（A）就是上述P（X=r）的概率，试验次数是n，生成的随机数如J列所示。具体到实例中，可以这样理解，假设总共有10个问题，每个问题都有4个选项，每回答对一题的概率是0.25，二项分布求的就是回答对r到题的概率，这里随机数模拟的就是回答对问题的题数。

 

三、伯努利

伯努利分布又叫0-1分布，是一个离散型的概率分布，是n=1的二项分布的特殊情况。它的变量为0和1，伯努利分布的期望E(X)=p，方差Var(X)=pq。

 

在随机数发生器中，要填的参数是P=1的概率，这里我们生成了1列100个随机数，数值只有0和1，其中p=1的概率为0.5

 

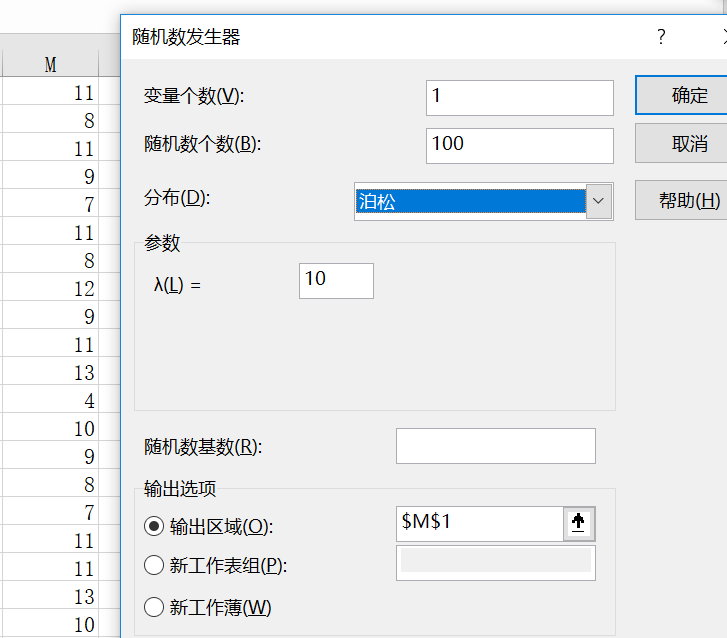
四、泊松

泊松分布的条件：

• 单独事件在给定区间内随机、独立地发生。给定区间可以是时间或空间。

• 已知该区间内的事件平均发生次数，且为有限数值。

泊松分布记做：X~Po(),X表示给定区间内事件发生的次数，求给定区间内发生r次事件的概率为：

泊松分布的期望E(X)=​，方差Var(X)=，泊松分布是离散型。

具体到随机数发生器中，我们生成1列100个随机数，参数就是上述图片所示，即给定区间内事件平均发生的次数或发生率，不一定非为整数，生成的随机数如K列所示。具体到实例中，可以这样理解，某加油站，平均每小时来加油的车辆为10辆，泊松分布求的这个加油站每小时前来加油的车辆次数的概率，这里随机数模拟的是每小时前来加油的车辆的辆数，共模拟100次。

 

五、正态

不同于二项分布和泊松分布，正态分布是连续型的分布，又叫高斯分布，正态分布通过参数平均值和方差确定。正态分布记做：X~N（）

在随机数发生器中，它的参数有两个：平均值和标准差。标准差是方差的平方根，方差是数值与均值的距离的平方数的平均值，方差已经可以体现数据的分散程度了，但标准差更直观。标准差越小，数值离均值越近，正态分布的曲线就越扁平、越宽。

我们生成1列100个随机数，这100个随机数符合标准的正态分布，平均值是0，标准差为1。

 

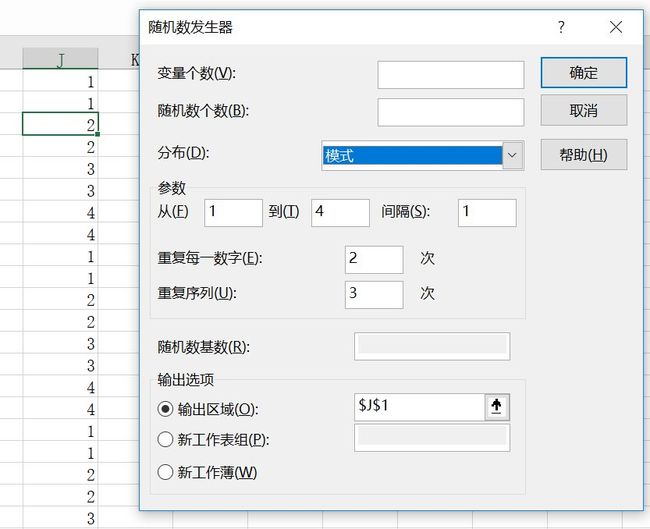
六、模式

以下界和上界、步幅、数值的重复率和序列的重复率来表征。EXCEL的“模式”所产生的重复序列是按相同步长产生的重复序列。

具体到随机数发生器里，下界是数值的最小值，上界是数值的最大值，步幅是该数字间隔，如1~4，间隔1，则按产生1、2、3、4产生随机数，间隔为2，则按1、3产生随机数。数值的重复率是每一数字重复几次，序列的重复率是该序列重复几次。如从1到4，间隔1，重复每一数字2次，重复序列3次，得到112233441122334411223344的随机数。

 

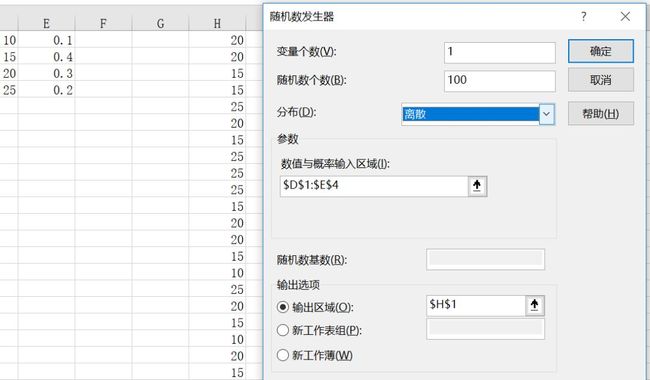
七、离散

离散的参数是输入数值与概率两列。左边一列是数值，右边一列是该数值发生的概率，且概率的和必须为1。如举例所示，离散随机数生成的是100个10、15、20、25这四个数字，见H列，其中10出现的概率为0.1,15出现的概率为0.4,20出现的概率为0.3,25出现的概率为0.2，见DE列，DE列是参数的输入区域。

 

至此，我们了解了用Excel如何生成随机数，同时顺便了解了生成的随机数的各项分布特征。下一小节将就生成的随机数进行频率分布直方图的做法详解。

 

下一节内容：用Excel做直方图（2）：频率分布直方图

 

@文章属原创，转载请联系作者

@作者：虾壳，在数据分析的道路上努力奔跑

@微信公众号：可乐的数据分析之路

往期文章精选：

用Excel做相关性分析

用Excel做排列图

数据处理

数据分析方法论

入门数据分析

我的2018年终总结分析