使用伪半监督学习的无监督聚类

提出两个问题：是否有可能仅使用无监督技术来创建半监督方法所需的小标签数据集？如果是这样，半监督方法是否可以利用这种自动生成的伪标记数据集来提供比最新的无监督方法更高的性能？
为了自主创建高精度的伪标记数据集，我们将深度网络的集成与自定义图聚类算法结合使用（第4节）。我们首先以无人监督的方式训练一组深层网络。每个网络独立地对输入进行聚类。然后，我们比较两个输入数据点。如果所有网络都同意这两个数据点属于同一群集，则可以合理确定这些数据点属于同一类。这样，我们以完全不受监督的方式高精度地识别了属于同一类的所有输入数据对。
在下一步中，我们将使用这些高质量的输入对生成一个相似度图，其中数据点是节点，数据集之间的边缘被我们的整体视为相似。
从该图中，我们提取出数据点的紧密簇，这些簇用作伪标签。请注意，在此步骤中，我们不对整个数据集进行聚类，而仅对我们可以在其上获得高精度的一小部分进行聚类。从该图中提取高质量的聚类，同时确保提取的聚类对应于不同的类别，这具有挑战性。我们将在4.2.1节中讨论解决此问题的方法。通过这种方式，我们的方法提取了属于每个类别的明确样本，用作半监督学习的伪标签。
对于使用上面生成的标签进行半监督学习，可以使用阶梯网络Rasmus等。 （2015）。但是，我们发现梯形网络不适合初始的无监督聚类步骤，因为它可以退化为在没有无监督损失的情况下为所有输入输出恒定值。为了实现无监督聚类，我们使用信息最大化Krause等人扩展了阶梯网络。 （2010）创建Ladder-IM，并以点积损失创建Ladder-Dot。在第5节中，我们表明Ladder-IM和Ladder-Dot本身也提供了对现有技术的改进。对于第一个无监督学习步骤以及随后的伪半监督迭代，我们使用相同的模型。
最终，迭代了使用集合查找高质量集群并将其用作标签来训练新的半监督模型集合的方法，从而产生了持续的改进。我们的方法的主要收益主要来自于这种迭代方法，在某些情况下，与基本的无监督模型相比，该方法的准确性最高可提高17％（请参见5.4节）。我们将我们的伪半监督学习方法命名为Kingdra1。 Kingdra与数据集的类型无关。我们将在第5节中展示其在图像和文本数据集上使用的示例。这与之前使用CNN的某些方法（例如Chang等。 （2017），Caron等。 （2018），专门针对图像数据集。我们使用Kingdra在几个标准图像（MNIST，CIFAR10，STL）和文本（路透社，20news）数据集上进行无监督分类。在所有这些数据集上，与当前最新的深度无监督聚类技术相比，Kingdra能够实现更高的聚类精度。
例如，在CIFAR10和20news数据集上，Kingdra能够分别实现54.6％和43.9％的分类准确率，比最先进的结果提供了8-12％的绝对增益。 （2017）;谢等。 （2016）。
之前生成伪标签的工作

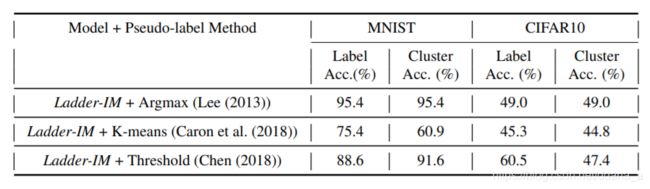
我们再次在新训练的模型上运行伪标签方法，以得出一组更新的伪标签。我们重复训练和伪标签的过程，直到伪标签的准确性稳定下来。我们将此称为最终聚类精度。表1显示了这三种方法的初始伪标签精度和最终聚类精度结果。首先，考虑MNIST。 Ladder-IM的无监督聚类准确性为95.4％。 Argmax只是根据模型的输出分配伪标签，并且由于它不会为后续迭代添加任何新信息，因此最终精度保持在95.4％。另一方面，通过K均值和阈值方法识别的伪标签会导致初始标签准确性较差（75.4％和88.6％）。当将此低准确性伪标签用作监督以进一步训练模型时，最终聚类准确性较低，分别为60.9％和91.6％。 CIFAR10结果相似。 Ladder-IM的聚类精度为49％，在Argmax下仍然与以前相同。使用K均值方法的伪标签准确性较差，导致最终准确性降低到44.8％。有趣的是，阈值会导致60.5％的初始准确度稍高一些，但即使这样也不够高，无法提高CIFAR10的最终聚类准确度。从这些结果，我们得出以下两个结论。首先，如果初始伪标签准确性不高，则使用伪标签作为监督对象可能会降低最终的聚类准确性。因此，初始伪标签的高精度对于提高聚类精度至关重要。第二，目前用于识别伪标签的方法无法提供很高的准确性，因此无法帮助提高整体聚类的准确性。
聚类相关工作
3相关工作
无监督学习
多年来，已经提出了各种无监督聚类方法。 Ng使用基于频谱聚类的方法，而Elhamifar使用稀疏子空间方法进行无监督学习。最近，已经提出了几种基于深度神经网络的方法，这些方法可以很好地扩展到大型数据集。深度神经网络学习高级表示的能力使其成为无监督学习的不错选择。 Coates和Caron使用卷积和k均值进行聚类。例如，Caron对从卷积网络中获得的特征进行聚类进行迭代，并使用这些聚类作为伪标签来训练分类器。作者没有报告聚类性能，并且我们观察到该方法很容易退化。 Chang使用基于成对点积的相似性来识别紧密的输入对，这些输入对提供了监控信号。但是，这些基于卷积的方法仅适用于图像数据集。 Xie同时使用深度神经网络学习特征表示和聚类分配，并同时处理图像和文本数据集。 Hu将正则化与互信息丢失相结合用于无监督学习，并获得了最先进的结果。作者在两种环境下进行实验-随机扰动训练和虚拟对抗训练。 Hjelm等其他作品使用互信息来最大化空间特征与非空间特征之间的互信息。 Ji使图像的预测标签和增强图像的预测标签之间的互信息最大化。此方法使用卷积网络，并且需要数据集的领域知识。
自我监督学习
无监督学习的另一种形式是使用辅助学习任务，可以自行生成标签以从数据生成有用的表示。许多方法使用图像块的空间信息来生成自我监督的数据。例如。 Pathak等。 （2016年）使用周围斑块预测图像斑块中的像素，而Doersch等人（2016年） （2015）预测图像补丁的相对位置。 Sermanet等。 （2018）使用时间作为从不同角度拍摄的视频之间的自我监控信号。时间信号还用于通过预测未来的帧（例如帧）来从单个视频中学习表示形式。登顿等。 （2017）。我们的方法使用整个集合中输入点的输出之间的相关性作为监控信号，以生成自我监督的伪标签。
半监督学习
半监督方法使用数据点的稀疏标记。 Szummer＆Jaakkola（2002）根据最近的邻居传播标签。韦斯顿等。 （2012年）使用了标签传播的深层版本。 Lee（2013）调整标签概率，从仅信任真实标签开始，逐渐增加伪标签的权重。 Rasmus等。 （2015年）采用降噪自动编码器架构，并表现出令人印象深刻的性能。 Tarvainen＆Valpola（2017）使用先前迭代的平均模型作为教师。除此之外，还有一些半监督的学习方法，例如Xie等。 （2019）和Berthelot等人。 （2019）使用数据扩充并假设数据集具有某些领域知识，以及一些特定于图像数据集的数据扩充。 Miyato等。 （2018）和Shinoda等。 （2017）使用虚拟对抗训练与分类损失相结合来执行半监督分类。但是，我们发现，如果我们在无人监督的情况下联合训练它们，这些方法将无法很好地发挥作用。梯形网络不需要任何依赖于域的扩充，可同时用于图像和文本数据集，并且可以轻松地联合进行监督和无监督损失的训练。因此，我们选择在实验中使用阶梯网络，尽管我们的方法足够通用，可以与任何采用无监督损失条件进行训练的半监督方法一起使用。
无监督的集成学习
无监督的集成学习主要限于生成一组聚类并将它们组合为最终聚类。黄等。 （2016）将集成聚类转化为二进制线性规划问题。 Wang等。 （2009）；弗雷德和詹恩（Fred＆Jain（2005））使用逐对共现方法来构建一个联合矩阵，并使用它来测量数据点之间的相似性。参见Vega-Pons和Ruiz-Shulcloper（2011）对整体聚类算法的调查。请注意，据我们所知，没有一种集成聚类算法采用像我们这样的半监督步骤，也没有利用深度网络。
框架
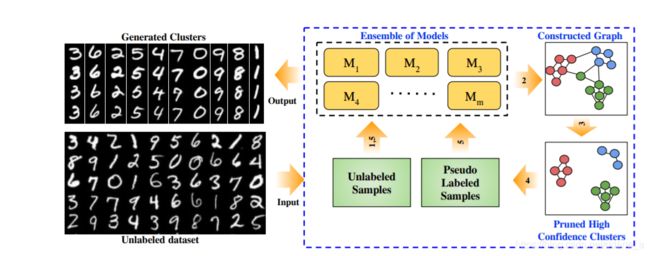在图1中概述了Kingdra方法。给定未标记的数据集X = {x1,…,xn}，我们从模型 M = {M1,…,Mm}的无监督训练开始。
对于单个模型，可以使用任何非监督模型。但是，我们提出了一种新颖的Ladder- *模型，该模型建立在Rasmus等人的梯形网络上。 （2015）并对其进行修改以支持群集。接下来，我们使用一对数据点上的集成模型之间的一致性作为度量数据点之间的相似性。该成对数据用于构建相似度图，从中我们提取k个紧密的数据点簇，这些簇用作伪标记。请注意，在此步骤中，我们不对整个数据集进行聚类，而仅对我们可以在其上获得高精度的一小部分进行聚类。如第2节所述，这对于提高我们的半监督训练的准确性非常重要。这些伪标签随后将用作Ladder- *模型新集合的半监督训练的训练数据。最后，我们对上述步骤进行了多次迭代，以进行持续改进。
BASE MODEL
我们方法的第一步是对模型集合进行无监督训练。我们的框架允许在此步骤中使用任何不受监督的方法，并且我们已经在尝试使用现有方法，例如IMSAT Hu(2017)。此基础模型的准确性直接影响最终模型的准确性，因此使用准确的基础模型显然会有所帮助。有鉴于此，我们还开发了一种新颖的无监督模型Ladder- *，其在大多数数据集中的表现均优于其他无监督模型。梯形网络Rasmus（2015）。在半监督环境下显示出巨大的成功。但是，据我们所知，梯形体系结构尚未用于无监督群集。可能的一个原因是，在没有监督损失项的情况下，梯形网络可以退化为所有输入输出恒定值。为了避免这种退化，我们在常规阶梯损失项中添加了无监督的损失，以便它指导网络为相似的输入提供相似的输出，但总体上使输出的多样性最大化，从而使相似的输入指向相似的输出。我们通过合并以下两种损失之一来实现此目标– IM损失Krause（2010）或点积损失Chang（2017）。我们分别将这两种变体称为Ladder-IM和Ladder-Dot。
IM损失：IM损失或信息最大化损失只是分类器的输入X和输出Y之间的相互信息：
I（X; Y）= H（Y）− H（Y | X）
其中H（）和H（|）分别是熵和条件熵。最大化边际熵项H（Y），鼓励网络为输入分配不同的类别，从而鼓励在输出类别上进行均匀分配。另一方面，最小化条件熵会鼓励给定输入的类别明确分配。
点积损失：点积损失定义为

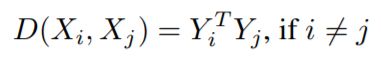
这就迫使不同输入的网络输出尽可能正交。这与IM丢失具有相似的效果，从而鼓励网络为输入分配不同的类别。
在Ladder-IM和Ladder-Dot中，我们发现Ladder-IM在大多数情况下的性能要优于Ladder-Dot。但是，我们确实发现，当数据集的每个类别的样本数量存在较大的不平衡时，梯形图点和Kingdra迭代的性能会更好。原因是，点积损失与每个类别的样本数无关，而IM损失中的边际熵项将驱使网络朝样本数较少的类别过度拟合。
无监督的集合
Kingdra利用Ladder- *模型的集成来进一步提高无监督学习的性能。请注意，在监督学习中，集成是微不足道的，因为我们可以简单地平均各个模型的输出或对它们进行投票。另一方面，在无监督学习中，进行投票并非易事，因为在没有训练标签的情况下，没有针对不同模型的输出进行稳定的类分配，因此我们没有任何模型的类ID映射到另一个。为了解决这个问题，我们提出了一种简单的方法，即查看数据点对，而不是单个样本。如果集合中的大多数（或全部）模型将两个数据点放在同一群集中，则两个数据点具有较高的置信度。例如，给定一个输入对x，x0，如果对于足够多的模型，Mi（x）= Mi（x0），我们可以很有把握地说它们属于同一类。使用这种成对方法，我们提出了一种基于图的方法来查找小型但高精度的聚类。
基于图形的小集群
我们用n个节点构造图G = {X，Epos，Eneg}，其中每个输入数据点x表示为一个节点。这里Epos和Eneg是图中的两种边缘类型：
•强优势：当大量模型在其预测类别上达成一致时，两个数据点之间会添加强优势。 （x，x0）∈Epos⇐⇒n_agree（x，x0）≥tpos其中tpos是选择的阈值，n_agree（x，x0）= | {m：m∈M，m（x）= m（x0）} |。
•强负边缘：当大量模型在其预测类别上存在分歧时，两个数据点之间会添加强负边缘。 （x，x0）∈Eneg⇐⇒n_disagree（x，x0）≥tneg，其中tneg是选定的阈值，n_disagree（x，x0）= | {m：m∈M，m（x）6 = m（x0 ）} |。
两个数据点之间的强上升沿表示大多数模型认为它们属于同一类别，而两个数据点之间的强下降沿表示大多数模型认为它们应该属于不同类别。

构建图后，每个强正边缘集团将是一个集群，其中集团内的数据点具有较高的置信度，属于同一类。由于我们仅向图添加高置信度边，因此，团的数量可能远大于k。因此，我们需要选择k个派系，在这些派系中我们要最大化每个派系的大小，但还要求派系是多样的（以便不选择两个数据点属于同一类的派系）。因此，在团内部，节点应通过强的正边缘连接，而在团之间，节点应通过强的负边缘连接。由于无法在多项式时间内找到团，因此我们使用了一种简单有效的贪婪近似算法，如算法1所示。我们没有贪心地找到具有最大正向边数的节点（第4行），而不是找到团。直觉是该节点的大多数邻居也将彼此连接。对于Cifar-10，我们发现在90％的阈值下，有81％的节点完全相互连接。如果阈值为100％，则群集中的所有节点都通过传递性相互连接。我们将具有最多数量的强正边缘的节点以及通过强正边缘连接至该节点的其他节点添加到群集中（第5行）。然后，我们删除所有对所选节点没有强烈负面影响的节点（第6-7行）。直觉是这些节点与所选集群的差异不够大（因为某些模型认为它们与当前所选节点属于同一类），因此不应成为下一组所选集群的一部分。通过重复该过程k次，我们得到了k个不同的簇，大致满足了我们的要求。
迭代训练
一旦确定了高精度聚类，我们将这些聚类点（集合S中的点）视为伪标记，并使用半监督方法解决我们的无监督聚类问题。尽管可以使用任何半监督方法，但如第4.1节所述，我们使用建议的Ladder- *方法，在实验中我们发现它优于梯形网络。我们不是训练单个半监督模型，而是训练一组模型，然后再次使用它们来找到高质量的聚类。可以迭代此方法，从而获得持续的改进。我们称这种方法为金德拉。算法2描述了完整的Kingdra算法。

首先，仅使用无监督的Ladder- *损失（第1-4行）来训练各个模型。然后，对于每个迭代，我们获得高精度聚类（第6行），从它们中获取伪标签（第8行），然后训练具有无监督损失和有监督损失的模型（第9-10行）。我们使用迷你簇计算伪标签，如下所示。对于模型Mj∈M和聚类S，我们需要找到聚类到模型输出类的适当映射。特别是，对于集群S0∈S，我们为S0中的所有数据点分配以下标签：

也就是说，我们将集群映射到输出类，集群中的大多数数据点都映射到该输出类。这些伪标签然后用于计算Ladder- *的监督损失。这种迭代方法导致聚类质量的不断提高。我们观察到，算法1返回的簇的大小在每次迭代后都会增加，直到它们几乎覆盖了整个输入集。正如我们在第5节中所展示的，模型的聚类性能通常会随着每次迭代的进行而提高，直到饱和为止，如第5节所示。我们还注意到，聚类分配在后续迭代中变得更加稳定，这也导致了多次运行的方差减少。也就是说，如果我们运行Kingdra进行更多迭代，则多次运行的方差会减小。
实验
在本节中，我们评估Kingdra在几个流行数据集上的性能。为了进行公平的比较，我们使用与之前的文献Hu等相同的数据预处理和模型层大小。
Weihua Hu, Takeru Miyato, Seiya Tokui, Eiichi Matsumoto, and Masashi Sugiyama. Learning discrete representations via information maximizing self augmented training. In ICML, 2017.
数据集
我们在三个图像数据集和两个文本数据集上评估Kingdra：MNIST是一个70000个手写数字的数据集，大小为28 x 28像素。此处，原始像素值被归一化为0-1范围，并被展平为784个维度的向量。 CIFAR10是一个32 x 32彩色图像的数据集，具有10个类，每个类具有6000个示例。 STL是96 x 96彩色图像的数据集，具有10个类，每个类具有1300个示例。对于CIFAR10和STL，原始像素不适合我们的目标，因为颜色信息占主导地位，因此如Hu等人所述。 （2017），我们使用从ImageNet数据集上经过预训练的Resnet-50网络中提取的特征。路透社是一个数据集，包含英语新闻报道，数据不平衡，分为四个类别。我们使用了与Hu等人相同的预处理方法。 （2017）;删除停用词后，使用了tf-idf功能。 20News是一个数据集，其中包含具有20个不同新闻组的新闻组文档。与Hu等类似。 （2017），我们删除停用词并保留2000个最常用词，并使用了tf-idf功能。我们所有的实验都是使用相同的预处理数据进行的。
比较
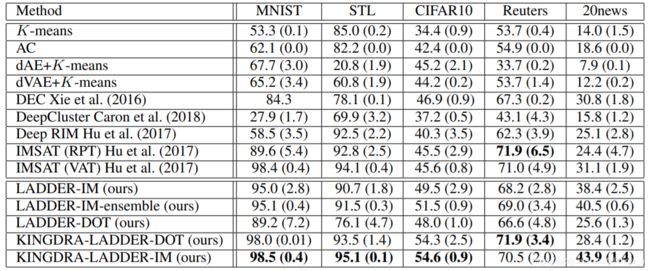
我们将Kingdra与数据集中的几种聚类算法进行了比较。具体来说，我们将其与传统聚类算法（例如K-Means和聚集聚类（AC））进行比较。我们还与表示学习基准进行了比较，在该学习表示基准上，我们使用诸如Deep Autoencoders（dAE），Deep Variational Auto encoders（dVAE）之类的模型，然后对学习的表示使用K-Means。最后，我们还将模型与基于深度学习的聚类方法（例如Deep RIM，DEC，DeepCluster和IMSAT）进行比较。深度RIM使用多层神经网络RIM的目标。 DEC迭代地学习低维特征表示并优化聚类目标。我们还比较了IMSAT的两个版本– IMSAT（RPT）和IMSAT（VAT），它们使用数据增强在模型输出中施加不变性。对于我们的结果，我们分别报告Ladder-IM和Ladder-Dot的性能，最后报告了包含Ladder- *网络集成以及半监督迭代的Kingdra。为了公平地比较，我们对所有基于神经网络的模型使用相同的网络体系结构。

结论
在本文中，我们介绍了Kingdra，这是一种新颖的伪半监督聚类学习方法。 Kingdra的表现优于当前基于无监督深度学习的最新技术，CIFAR10和20news数据集的绝对准确度提高了8-12％。作为Kingdra的一部分，我们提出了群集阶梯网络Ladder-IM和Ladder-Dot，它们在无监督和半监督环境下均能很好地工作。
讨论
尽管Kingdra在我们研究的数据集中表现良好，但是随着类数的增加，所使用的基于相似度的图聚类算法会遇到困难。例如，对于我们评估的数据集，可以简单地将tpos和tneg设置为集合中的模型数。但是，随着类数量的增加，这些阈值可能需要进行一些调整。对于具有100个类别的CIFAR100，我们的图聚类算法无法有效识别100个不同的类别。我们正在考虑改进聚类算法，作为未来工作的一部分。我们还正在评估通过更改模型的结构，大小和/或更改梯形网络中使用的随机噪声的标准偏差，为集成中的模型增加多样性。