VTK笔记——空间几何变换(Transform)，平移、旋转和缩放

先看一张图，下图是一个三维的Cow,

试想在使用中，是否会遇到如下场景？

1.将Cow移动到某个位置

2.旋转Cow到背面

3.想看清楚Cow面部的细节，改变它大小等等

可能你会说，这还不简单，通过操作相机就好了。操作相机，使得相机的空间位置发生了变化，但对三维物体的空间位置并没有改变，要想改变模型的空间位置，就需要对模形本身做空间变换。

空间变换的基础知识

变换矩阵（Transformation Matrices）

我们知道，在屏幕上显示的是二维的图形，三维图形都是投影到二维平面的，但它们定义在三维空间的。空间变换的基本元素都是三维坐标点，在计算机图形学中，三维坐标点用齐次坐标表示。利用其次坐标，可以将空间变换用4x4的矩阵来表示。这些变换都可以用矩阵的运算完成。

 

VTK有关空间变换的类和方法

VTK相关的类有：

vtkTransform, vtkTransformFilter, vtkMatrix4x4等

相关的方法有：

• RotateX(angle)、RotateY(angle)、RotateZ(angle)

• RotateWXYZ(angle,x,y,z)

• Scale(x,y,z)

• Translate(x,y,z)

• SetMatrix(m)、GetMatrix(m)

• PostMultiply()、PreMultiply()

• SetPosition(x,y,z)、GetPosition(x,y,z)

• SetOrientation(x,y,z)、 GetOrientation(x,y,z)

• SetScale(sx,sy,sz)

• SetOrigin(x,y,z)、GetOrigin

 

下面通过几个场景来看看上面的一些类和方法是如何使用以及一些常见的问题。

[图1 圆锥体位于(0,0,0)，坐标轴向量长度为1个单位]

场景一：矩阵的顺序问题

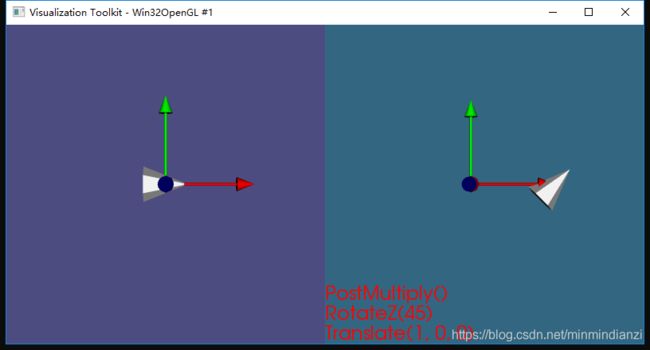
我们要对图1中位于世界坐标系原点的圆锥体做如下操作：

1. 圆锥体在X轴正方向上移动1个单位

2.绕Z轴旋转

vtkSmartPointer trans = 
	vtkSmartPointer::New();
trans->PostMultiply();
trans->Translate(1, 0, 0);
trans->RotateZ(45);
coneActor->SetUserTransform(trans);

试着改变一下1, 2两步的顺序：

对比来看，是两个不同的结果。而这个结果正是因为矩阵乘法并不满足交换定律。

因此，在使用时，进行变换的顺序非常重要，将对结果产生直接的影响。

对于变换矩阵，VTK是用以下顺序来应用这些变化的：

1. 移动actor到它的origin，缩放和旋转都是基于这个点完成的。

2. 缩放几何体。

3.actor依次绕Y, X和Z轴旋转。

4.从旋转中心移回到原来的位置后再移动actor到最终的位置。

在VTK中，矩阵乘法默认是左乘，即PreMultiply，上面的公式也遵循这个原则。为了便于理解，示例代码特地使用了右乘PostMultiply.

场景二：GetMatrix和GetUserMatrix的区别

Code1:

coneActor->RotateZ(45);
coneActor->SetPosition(1, 0, 0);

 

Code2:

trans->RotateZ(45);
trans->Translate(1, 0, 0);
coneActor->SetUserTransform(trans);

从两个结果可以看出，GetMatix和GetUserMatrix都是获取变换矩阵。所不同的是：

GetMatrix始终都可以获取到值，也就是说它得到的是圆锥体在世界坐标系的变换矩阵。

GetUserMatrix在Code2中获取到了值，而在Code1中得到是NULL，这说明它获取的是用户设置的变换矩阵。

注：GetUserMatrix、SetUserMatrix和GetUserTransform、SetUserTransform具有相同的作用。

完整示例代码

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

int main(int, char *[])
{
	vtkSmartPointer sphereSource =
		vtkSmartPointer::New();
	sphereSource->SetRadius(0.1);
	sphereSource->Update();

	vtkSmartPointer sphereMapper =
		vtkSmartPointer::New();
	sphereMapper->SetInputConnection(sphereSource->GetOutputPort());

	vtkSmartPointer sphereActor =
		vtkSmartPointer::New();
	sphereActor->SetPosition(0, 0, 0);
	sphereActor->SetMapper(sphereMapper);
	sphereActor->GetProperty()->SetColor(1, 0, 0);

	vtkSmartPointer coneSource =
		vtkSmartPointer::New();
	coneSource->SetRadius(.2);
	coneSource->SetHeight(.5);
	coneSource->SetCenter(0, 0, 0);
	vtkSmartPointer coneMapper =
		vtkSmartPointer::New();
	coneMapper->SetInputConnection(coneSource->GetOutputPort());
	vtkSmartPointer coneActor =
		vtkSmartPointer::New();
	coneActor->SetMapper(coneMapper);

	vtkSmartPointer oriConeActor =
		vtkSmartPointer::New();
	oriConeActor->SetMapper(coneMapper);
#define AXIS_LEN 1.
	vtkSmartPointer oriAxesActor =
		vtkSmartPointer::New();
	oriAxesActor->SetPosition(0, 0, 0);
	oriAxesActor->SetTotalLength(AXIS_LEN, AXIS_LEN, AXIS_LEN);
	oriAxesActor->SetShaftType(0);
	oriAxesActor->SetAxisLabels(0);
	oriAxesActor->SetCylinderRadius(0.02);

	vtkSmartPointer axesActor =
		vtkSmartPointer::New();
	axesActor->SetPosition(0, 0, 0);
	axesActor->SetTotalLength(AXIS_LEN, AXIS_LEN, AXIS_LEN);
	axesActor->SetShaftType(0);
	axesActor->SetAxisLabels(0);
	axesActor->SetCylinderRadius(0.02);

	vtkSmartPointer textActor = 
		vtkSmartPointer::New();
	textActor->SetPosition2(100, 40);
	textActor->GetTextProperty()->SetFontSize(24);
	textActor->GetTextProperty()->SetColor(1, 0, 0);


	vtkSmartPointer trans = 
		vtkSmartPointer::New();

#if 0
	trans->PostMultiply();

	coneActor->SetPosition(1, 0, 0);
	//trans->Translate(1, 0, 0);
	//trans->RotateZ(45);
	trans->RotateZ(45);
	trans->Translate(1, 0, 0);
	coneActor->SetUserTransform(trans);
	//textActor->SetInput("PostMultiply()\nTranslate(1, 0, 0)\nRotateZ(45)");
	textActor->SetInput("PostMultiply()\nRotateZ(45)\nTranslate(1, 0, 0)");
#endif

#if 1
	//coneActor->RotateZ(45);
	//coneActor->SetPosition(1, 0, 0);
	//textActor->SetInput("coneActor->RotateZ(45)\nconeActor->SetPosition(1, 0, 0)");

	trans->RotateZ(45);
	trans->Translate(1, 0, 0);
	coneActor->SetUserTransform(trans);
	textActor->SetInput("trans->RotateZ(45)\ntrans->Translate(1, 0, 0)\nconeActor->SetUserTransform(trans)");

	cout << "GetMatrix:" << endl;
	if (coneActor->GetMatrix()!=NULL)
	{
		coneActor->GetMatrix()->Print(cout);
	}
	else
	{
		cout << "NULL" << endl;
	}
	cout << "GetUserMatrix:" << endl;
	if (coneActor->GetUserMatrix() !=NULL)
	{
		coneActor->GetUserMatrix()->Print(cout);
	}
	else
	{
		cout << "NULL" << endl;
	}
	//cout << "GetUserTransform:" << endl;
	//if (coneActor->GetUserTransform() !=NULL)
	//{
	//	coneActor->GetUserTransform()->Print(cout);
	//}
	//else
	//{
	//	cout << "NULL" << endl;
	//}
#endif
	vtkSmartPointer renderer1 =
		vtkSmartPointer::New();
	vtkSmartPointer renderer2 =
		vtkSmartPointer::New();

	vtkSmartPointer renderWindow =
		vtkSmartPointer::New();
	renderWindow->SetSize(800, 400);
	renderWindow->AddRenderer(renderer1);
	renderWindow->AddRenderer(renderer2);
	vtkSmartPointer renderWindowInteractor =
		vtkSmartPointer::New();
	renderWindowInteractor->SetRenderWindow(renderWindow);

	double leftViewport[] = { 0.0, 0.0, 0.5, 1.0 };
	double rightViewport[] = { 0.5, 0.0, 1.0, 1.0 };

	renderer1->AddActor(oriAxesActor);
	renderer1->AddActor(sphereActor);
	renderer1->AddActor(oriConeActor);
	renderer2->AddActor(axesActor);
	renderer2->AddActor(sphereActor);
	renderer2->AddActor(coneActor);
	renderer2->AddActor2D(textActor);
	renderer1->SetBackground(.3, .3, .5);
	renderer2->SetBackground(.2, .4, .5);
	renderer1->SetViewport(leftViewport);
	renderer2->SetViewport(rightViewport);

	renderWindow->Render();
	renderWindowInteractor->Start();

	return EXIT_SUCCESS;
}

Reference

VTK中模型的旋转与平移

三维空间几何变换原理[平移、旋转、错切]